Menu Close

Question-51558

Tinku Tara 0 Comments
Pin




Question Number 51558 by Tawa1 last updated on 28/Dec/18
Commented by Tawa1 last updated on 28/Dec/18
Please help.
$$\mathrm{Please}\:\mathrm{help}. \\ $$
Commented by Kunal12588 last updated on 28/Dec/18
Commented by Tawa1 last updated on 28/Dec/18
God bless you sir.
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Answered by mr W last updated on 28/Dec/18
Commented by Tawa1 last updated on 28/Dec/18
I reall appreciate your time sir. God bless you sir
$$\mathrm{I}\:\mathrm{reall}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{time}\:\mathrm{sir}.\:\:\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by mr W last updated on 28/Dec/18
let AB=1 AC=((sin 60°)/(sin 75°))=0.897 BC=((sin 45°)/(sin 75°))=0.732 ED=((AB)/2)=0.5 DF=((AC)/2)=0.448 FE=((BC)/2)=0.366 OE=OH=OG=OD=OI=OF=R =((0.5×0.448×0.366)/( (√((0.5+0.448+0.366)(−0.5+0.448+0.366)(0.5−0.448+0.366)(0.5+0.448−0.366)))))=0.259 sin (∠FOD/2)=((FD)/(2R))=((0.448)/(2×0.259)) ⇒∠FOF=119.734° ∠FID=180°−119.734°/2=120.133° ∠BDI=120.133−60=60.133° ∠BID=180−120.133=59.867° DI=((sin 60°)/(sin 59.867°))×((BC)/2)=0.366 BI=((sin 60.133°)/(sin 59.867°))×((BC)/2)=0.367 FI=FB−BI=0.5−0.367=0.133 sin ((∠EOD)/2)=((ED)/(2R))=((0.5)/(2×0.259)) ⇒∠EOD=149.702° 45+60−x/2=149/2 ∠HOG=2(45+60)−149.702=60.297° HG=2R sin ((60.297°)/2)=0.260 ∠EOH=2×60−60.297=59.703° EH=2R sin ((59.703°)/2)=0.258 ∠DOG=2×45−60.297=29.703° DG=2R sin ((29.703°)/2)=0.133 Area of hexagon A_H A_H =(1/4)(0.366×(√(4×0.259^2 −0.366^2 )) +0.258×(√(4×0.259^2 −0.258^2 )) +0.260×(√(4×0.259^2 −0.260^2 )) +0.133×(√(4×0.259^2 −0.133^2 )) +0.366×(√(4×0.259^2 −0.366^2 )) +0.133×(√(4×0.259^2 −0.133^2 ))) =(1/4)(0.134+0.116+0.116+0.067+0.134+0.067) =0.159 Area of triangle A_T A_T =(1/2)×1×0.897×sin 45°=0.317 ⇒((Area hexagon)/(Area triangle))=((0.159)/(0.317))=0.50
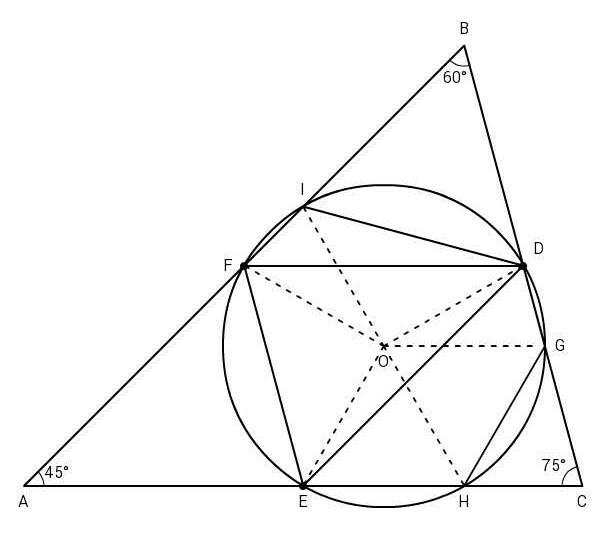
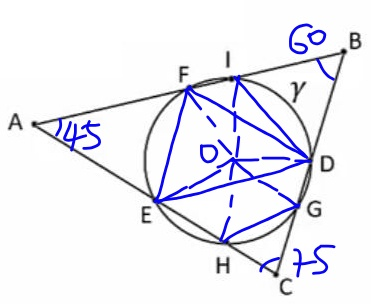
$${let}\:{AB}=\mathrm{1} \\ $$$${AC}=\frac{\mathrm{sin}\:\mathrm{60}°}{\mathrm{sin}\:\mathrm{75}°}=\mathrm{0}.\mathrm{897} \\ $$$${BC}=\frac{\mathrm{sin}\:\mathrm{45}°}{\mathrm{sin}\:\mathrm{75}°}=\mathrm{0}.\mathrm{732} \\ $$$${ED}=\frac{{AB}}{\mathrm{2}}=\mathrm{0}.\mathrm{5} \\ $$$${DF}=\frac{{AC}}{\mathrm{2}}=\mathrm{0}.\mathrm{448} \\ $$$${FE}=\frac{{BC}}{\mathrm{2}}=\mathrm{0}.\mathrm{366} \\ $$$${OE}={OH}={OG}={OD}={OI}={OF}={R} \\ $$$$=\frac{\mathrm{0}.\mathrm{5}×\mathrm{0}.\mathrm{448}×\mathrm{0}.\mathrm{366}}{\:\sqrt{\left(\mathrm{0}.\mathrm{5}+\mathrm{0}.\mathrm{448}+\mathrm{0}.\mathrm{366}\right)\left(−\mathrm{0}.\mathrm{5}+\mathrm{0}.\mathrm{448}+\mathrm{0}.\mathrm{366}\right)\left(\mathrm{0}.\mathrm{5}−\mathrm{0}.\mathrm{448}+\mathrm{0}.\mathrm{366}\right)\left(\mathrm{0}.\mathrm{5}+\mathrm{0}.\mathrm{448}−\mathrm{0}.\mathrm{366}\right)}}=\mathrm{0}.\mathrm{259} \\ $$$$\mathrm{sin}\:\left(\angle{FOD}/\mathrm{2}\right)=\frac{{FD}}{\mathrm{2}{R}}=\frac{\mathrm{0}.\mathrm{448}}{\mathrm{2}×\mathrm{0}.\mathrm{259}} \\ $$$$\Rightarrow\angle{FOF}=\mathrm{119}.\mathrm{734}° \\ $$$$\angle{FID}=\mathrm{180}°−\mathrm{119}.\mathrm{734}°/\mathrm{2}=\mathrm{120}.\mathrm{133}° \\ $$$$\angle{BDI}=\mathrm{120}.\mathrm{133}−\mathrm{60}=\mathrm{60}.\mathrm{133}° \\ $$$$\angle{BID}=\mathrm{180}−\mathrm{120}.\mathrm{133}=\mathrm{59}.\mathrm{867}° \\ $$$${DI}=\frac{\mathrm{sin}\:\mathrm{60}°}{\mathrm{sin}\:\mathrm{59}.\mathrm{867}°}×\frac{{BC}}{\mathrm{2}}=\mathrm{0}.\mathrm{366} \\ $$$${BI}=\frac{\mathrm{sin}\:\mathrm{60}.\mathrm{133}°}{\mathrm{sin}\:\mathrm{59}.\mathrm{867}°}×\frac{{BC}}{\mathrm{2}}=\mathrm{0}.\mathrm{367} \\ $$$${FI}={FB}−{BI}=\mathrm{0}.\mathrm{5}−\mathrm{0}.\mathrm{367}=\mathrm{0}.\mathrm{133} \\ $$$$\mathrm{sin}\:\frac{\angle{EOD}}{\mathrm{2}}=\frac{{ED}}{\mathrm{2}{R}}=\frac{\mathrm{0}.\mathrm{5}}{\mathrm{2}×\mathrm{0}.\mathrm{259}} \\ $$$$\Rightarrow\angle{EOD}=\mathrm{149}.\mathrm{702}° \\ $$$$\mathrm{45}+\mathrm{60}−{x}/\mathrm{2}=\mathrm{149}/\mathrm{2} \\ $$$$\angle{HOG}=\mathrm{2}\left(\mathrm{45}+\mathrm{60}\right)−\mathrm{149}.\mathrm{702}=\mathrm{60}.\mathrm{297}° \\ $$$${HG}=\mathrm{2}{R}\:\mathrm{sin}\:\frac{\mathrm{60}.\mathrm{297}°}{\mathrm{2}}=\mathrm{0}.\mathrm{260} \\ $$$$\angle{EOH}=\mathrm{2}×\mathrm{60}−\mathrm{60}.\mathrm{297}=\mathrm{59}.\mathrm{703}° \\ $$$${EH}=\mathrm{2}{R}\:\mathrm{sin}\:\frac{\mathrm{59}.\mathrm{703}°}{\mathrm{2}}=\mathrm{0}.\mathrm{258} \\ $$$$\angle{DOG}=\mathrm{2}×\mathrm{45}−\mathrm{60}.\mathrm{297}=\mathrm{29}.\mathrm{703}° \\ $$$${DG}=\mathrm{2}{R}\:\mathrm{sin}\:\frac{\mathrm{29}.\mathrm{703}°}{\mathrm{2}}=\mathrm{0}.\mathrm{133} \\ $$$${Area}\:{of}\:{hexagon}\:{A}_{{H}} \\ $$$${A}_{{H}} =\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{0}.\mathrm{366}×\sqrt{\mathrm{4}×\mathrm{0}.\mathrm{259}^{\mathrm{2}} −\mathrm{0}.\mathrm{366}^{\mathrm{2}} }\right. \\ $$$$+\mathrm{0}.\mathrm{258}×\sqrt{\mathrm{4}×\mathrm{0}.\mathrm{259}^{\mathrm{2}} −\mathrm{0}.\mathrm{258}^{\mathrm{2}} } \\ $$$$+\mathrm{0}.\mathrm{260}×\sqrt{\mathrm{4}×\mathrm{0}.\mathrm{259}^{\mathrm{2}} −\mathrm{0}.\mathrm{260}^{\mathrm{2}} } \\ $$$$+\mathrm{0}.\mathrm{133}×\sqrt{\mathrm{4}×\mathrm{0}.\mathrm{259}^{\mathrm{2}} −\mathrm{0}.\mathrm{133}^{\mathrm{2}} } \\ $$$$+\mathrm{0}.\mathrm{366}×\sqrt{\mathrm{4}×\mathrm{0}.\mathrm{259}^{\mathrm{2}} −\mathrm{0}.\mathrm{366}^{\mathrm{2}} } \\ $$$$\left.+\mathrm{0}.\mathrm{133}×\sqrt{\mathrm{4}×\mathrm{0}.\mathrm{259}^{\mathrm{2}} −\mathrm{0}.\mathrm{133}^{\mathrm{2}} }\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{0}.\mathrm{134}+\mathrm{0}.\mathrm{116}+\mathrm{0}.\mathrm{116}+\mathrm{0}.\mathrm{067}+\mathrm{0}.\mathrm{134}+\mathrm{0}.\mathrm{067}\right) \\ $$$$=\mathrm{0}.\mathrm{159} \\ $$$${Area}\:{of}\:{triangle}\:{A}_{{T}} \\ $$$${A}_{{T}} =\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{1}×\mathrm{0}.\mathrm{897}×\mathrm{sin}\:\mathrm{45}°=\mathrm{0}.\mathrm{317} \\ $$$$\Rightarrow\frac{{Area}\:{hexagon}}{{Area}\:{triangle}}=\frac{\mathrm{0}.\mathrm{159}}{\mathrm{0}.\mathrm{317}}=\mathrm{0}.\mathrm{50} \\ $$
Commented by Tawa1 last updated on 28/Dec/18
God bless you sir.
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by Tawa1 last updated on 28/Dec/18
Is that the final answer sir
$$\mathrm{Is}\:\mathrm{that}\:\mathrm{the}\:\mathrm{final}\:\mathrm{answer}\:\mathrm{sir} \\ $$
Commented by Tawa1 last updated on 28/Dec/18
When you are free, help me finish it sir. I will study it. Thanks for your time
$$\mathrm{When}\:\mathrm{you}\:\mathrm{are}\:\mathrm{free},\:\mathrm{help}\:\mathrm{me}\:\mathrm{finish}\:\mathrm{it}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{will}\:\mathrm{study}\:\mathrm{it}.\:\mathrm{Thanks} \\ $$$$\mathrm{for}\:\mathrm{your}\:\mathrm{time} \\ $$
Commented by peter frank last updated on 28/Dec/18
very nice work sir.
$${very}\:{nice}\:{work}\:{sir}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *