Menu Close

Question-51700

Tinku Tara 0 Comments
Pin




Question Number 51700 by mr W last updated on 29/Dec/18
Commented by mr W last updated on 29/Dec/18
A rope with uniform mass is fixed at one end on point A. At point B the rope is laid over a pulley. All contact is frictionless and the size of pulley is negligible. Find the minimum length of the rope such that the rope remains in equilibrium as shown in the picture.
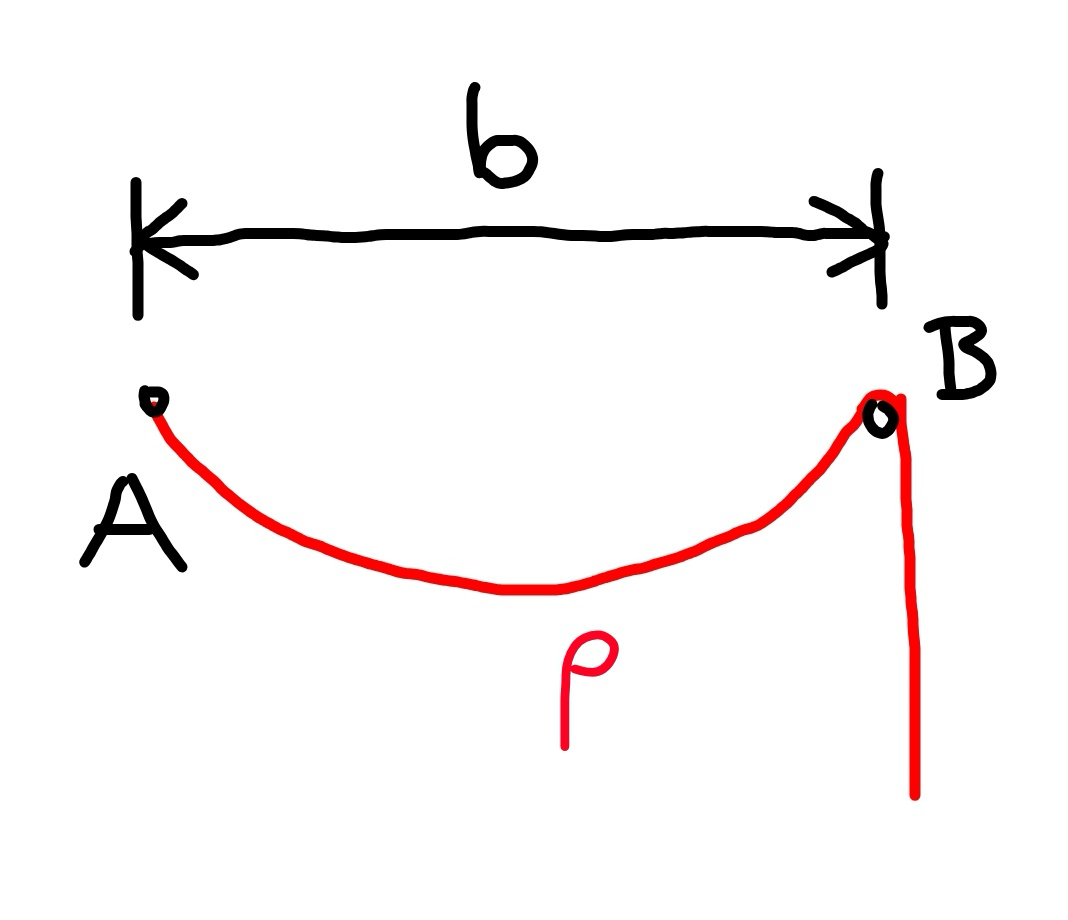
$${A}\:{rope}\:{with}\:{uniform}\:{mass}\:{is}\:{fixed} \\ $$$${at}\:{one}\:{end}\:{on}\:{point}\:{A}.\:{At}\:{point}\:{B}\:{the} \\ $$$${rope}\:{is}\:{laid}\:{over}\:{a}\:{pulley}.\:{All}\:{contact} \\ $$$${is}\:{frictionless}\:{and}\:{the}\:{size}\:{of}\:{pulley} \\ $$$${is}\:{negligible}. \\ $$$${Find}\:{the}\:{minimum}\:{length}\:{of}\:{the}\:{rope} \\ $$$${such}\:{that}\:{the}\:{rope}\:{remains}\:{in} \\ $$$${equilibrium}\:{as}\:{shown}\:{in}\:{the}\:{picture}. \\ $$
Answered by mr W last updated on 30/Dec/18
Commented by mr W last updated on 30/Dec/18
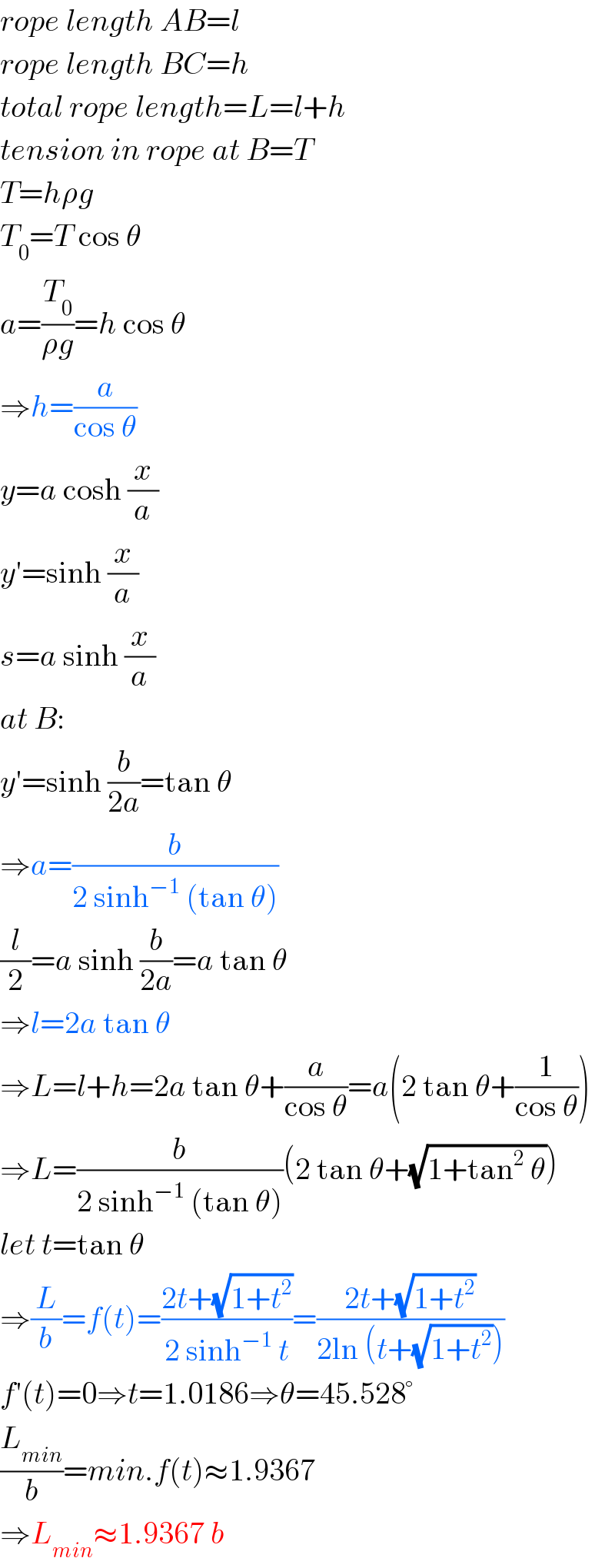
rope length AB=l rope length BC=h total rope length=L=l+h tension in rope at B=T T=hρg T_0 =T cos θ a=(T_0 /(ρg))=h cos θ ⇒h=(a/(cos θ)) y=a cosh (x/a) y′=sinh (x/a) s=a sinh (x/a) at B: y′=sinh (b/(2a))=tan θ ⇒a=(b/(2 sinh^(−1) (tan θ))) (l/2)=a sinh (b/(2a))=a tan θ ⇒l=2a tan θ ⇒L=l+h=2a tan θ+(a/(cos θ))=a(2 tan θ+(1/(cos θ))) ⇒L=(b/(2 sinh^(−1) (tan θ)))(2 tan θ+(√(1+tan^2 θ))) let t=tan θ ⇒(L/b)=f(t)=((2t+(√(1+t^2 )))/(2 sinh^(−1) t))=((2t+(√(1+t^2 )))/(2ln (t+(√(1+t^2 ))))) f′(t)=0⇒t=1.0186⇒θ=45.528° (L_(min) /b)=min.f(t)≈1.9367 ⇒L_(min) ≈1.9367 b
$${rope}\:{length}\:{AB}={l} \\ $$$${rope}\:{length}\:{BC}={h} \\ $$$${total}\:{rope}\:{length}={L}={l}+{h} \\ $$$${tension}\:{in}\:{rope}\:{at}\:{B}={T} \\ $$$${T}={h}\rho{g} \\ $$$${T}_{\mathrm{0}} ={T}\:\mathrm{cos}\:\theta \\ $$$${a}=\frac{{T}_{\mathrm{0}} }{\rho{g}}={h}\:\mathrm{cos}\:\theta \\ $$$$\Rightarrow{h}=\frac{{a}}{\mathrm{cos}\:\theta} \\ $$$${y}={a}\:\mathrm{cosh}\:\frac{{x}}{{a}} \\ $$$${y}'=\mathrm{sinh}\:\frac{{x}}{{a}} \\ $$$${s}={a}\:\mathrm{sinh}\:\frac{{x}}{{a}} \\ $$$${at}\:{B}: \\ $$$${y}'=\mathrm{sinh}\:\frac{{b}}{\mathrm{2}{a}}=\mathrm{tan}\:\theta \\ $$$$\Rightarrow{a}=\frac{{b}}{\mathrm{2}\:\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\theta\right)} \\ $$$$\frac{{l}}{\mathrm{2}}={a}\:\mathrm{sinh}\:\frac{{b}}{\mathrm{2}{a}}={a}\:\mathrm{tan}\:\theta \\ $$$$\Rightarrow{l}=\mathrm{2}{a}\:\mathrm{tan}\:\theta \\ $$$$\Rightarrow{L}={l}+{h}=\mathrm{2}{a}\:\mathrm{tan}\:\theta+\frac{{a}}{\mathrm{cos}\:\theta}={a}\left(\mathrm{2}\:\mathrm{tan}\:\theta+\frac{\mathrm{1}}{\mathrm{cos}\:\theta}\right) \\ $$$$\Rightarrow{L}=\frac{{b}}{\mathrm{2}\:\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\theta\right)}\left(\mathrm{2}\:\mathrm{tan}\:\theta+\sqrt{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\theta}\right) \\ $$$${let}\:{t}=\mathrm{tan}\:\theta \\ $$$$\Rightarrow\frac{{L}}{{b}}={f}\left({t}\right)=\frac{\mathrm{2}{t}+\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }}{\mathrm{2}\:\mathrm{sinh}^{−\mathrm{1}} \:{t}}=\frac{\mathrm{2}{t}+\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }}{\mathrm{2ln}\:\left({t}+\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }\right)} \\ $$$${f}'\left({t}\right)=\mathrm{0}\Rightarrow{t}=\mathrm{1}.\mathrm{0186}\Rightarrow\theta=\mathrm{45}.\mathrm{528}° \\ $$$$\frac{{L}_{{min}} }{{b}}={min}.{f}\left({t}\right)\approx\mathrm{1}.\mathrm{9367} \\ $$$$\Rightarrow{L}_{{min}} \approx\mathrm{1}.\mathrm{9367}\:{b} \\ $$
Commented by ajfour last updated on 30/Dec/18
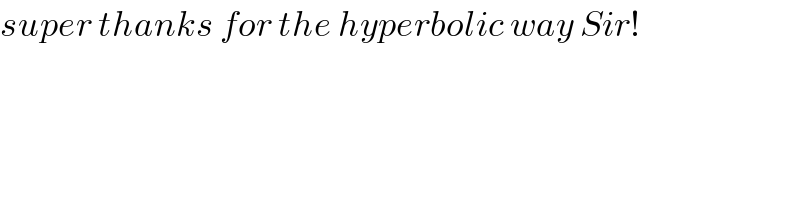
super thanks for the hyperbolic way Sir!
$${super}\:{thanks}\:{for}\:{the}\:{hyperbolic}\:{way}\:{Sir}! \\ $$
Commented by ajfour last updated on 30/Dec/18
Tcos θ=T_0 =T_B cos α ⇒ dTcos θ = Tsin θdθ ⇒ dT = ((Tsin θdθ)/(cos θ)) ...(i) Also (T+dT)sin (θ+dθ)−Tsin θ=ρgdl ⇒ dTsin θ+Tcos θdθ = ρgdl using (i): ((Tsin^2 θdθ)/(cos θ))+Tcos θdθ = ρgdl ⇒ Tdθ = ρgcos θdl = ρgdx ...(ii) and T_B sin α = ρg((l/2)) ...(iii) ⇒ ((Tcos θdθ)/(cos θ)) = ρgdx or (((T_B cos α)sin α)/(cos θ.sin α))dθ = ρgdx using (iii) ((ρg((l/2))cos α)/(cos θ.sin α))dθ = ρgdx (l/2)((cos α)/(sin α))∫_0 ^( θ) sec θ = x ⇒ ln(sec θ+tan θ)= ((2xtan α)/l) (√(1+((dy/dx))^2 ))+(dy/dx) = e^((2xtan α)/l) squaring 1= e^((4xtan α)/l) −2((dy/dx))e^((2xtan α)/l) ⇒ (dy/dx) = (1/2)(e^((2xtan α)/l) −e^(−((2xtan α)/l)) ) and this at B (x=(b/2)), gives 2tan α = e^((btan α)/l) −e^(−((btan α)/l)) 2m= t−(1/t) (say) ⇒ t^2 −2mt −1 = 0 or (t−m)^2 = 1+m^2 t = e^((bm)/l) = m+(√(1+m^2 )) ⇒ ((btan α)/l) = ln( tan α+sec α) ...(I) further T_B = 𝛒gz = ((𝛒gl)/(2sin 𝛂)) or z = (l/(2sin α)) (z being the vertically hanging length) L = l+z = l(1+(1/(2sin α))) and from (I) (4 lines above) L = ((btan α)/(ln(tan α+sec α)))(((2sin α+1)/(2sin α))) L = ((b(2sin α+1))/(2cos α ln(tan α+sec α))) ...(A) ⇒ (b/(2L)) = ((cos α ln(tan α+sec α))/((2sin α+1))) (d/dα)((b/(2L))) = 0 ⇒ ((cos α)/((2sin α+1)))×sec α +(((2sin α+1)(−sin α)−2cos^2 α)/((2sin α+1)^2 )) ln(tan α+sec α)= 0 ___________________________ ⇒ ln(sec α+tan α)= ((2sin α+1)/(2+sin α)) ..(B) ⇒ { α = 45.5274° } ___________________________ utilizing this in (A) L = ((b(2sin α+1))/(2cos α))×(((2+sin α))/((2sin α+1))) ⇒ L = ((b(2+sin α))/(2cos α)) = 1.9367b .
$${T}\mathrm{cos}\:\theta={T}_{\mathrm{0}} ={T}_{{B}} \mathrm{cos}\:\alpha \\ $$$$\Rightarrow\:{dT}\mathrm{cos}\:\theta\:=\:{T}\mathrm{sin}\:\theta{d}\theta \\ $$$$\Rightarrow\:{dT}\:=\:\frac{{T}\mathrm{sin}\:\theta{d}\theta}{\mathrm{cos}\:\theta}\:\:\:\:…\left({i}\right) \\ $$$${Also} \\ $$$$\:\:\:\:\:\left({T}+{dT}\right)\mathrm{sin}\:\left(\theta+{d}\theta\right)−{T}\mathrm{sin}\:\theta=\rho{gdl} \\ $$$$\Rightarrow\:{dT}\mathrm{sin}\:\theta+{T}\mathrm{cos}\:\theta{d}\theta\:=\:\rho{gdl} \\ $$$${using}\:\left({i}\right): \\ $$$$\:\:\:\:\:\:\frac{{T}\mathrm{sin}\:^{\mathrm{2}} \theta{d}\theta}{\mathrm{cos}\:\theta}+{T}\mathrm{cos}\:\theta{d}\theta\:=\:\rho{gdl} \\ $$$$\Rightarrow\:\:{Td}\theta\:=\:\rho{g}\mathrm{cos}\:\theta{dl}\:=\:\rho{gdx}\:\:\:…\left({ii}\right) \\ $$$$\:\:\:{and}\:\:\:{T}_{{B}} \mathrm{sin}\:\alpha\:=\:\rho{g}\left(\frac{{l}}{\mathrm{2}}\right)\:\:\:…\left({iii}\right) \\ $$$$\Rightarrow\:\:\frac{{T}\mathrm{cos}\:\theta{d}\theta}{\mathrm{cos}\:\theta}\:=\:\rho{gdx} \\ $$$${or}\:\:\:\:\:\:\frac{\left({T}_{{B}} \mathrm{cos}\:\alpha\right)\mathrm{sin}\:\alpha}{\mathrm{cos}\:\theta.\mathrm{sin}\:\alpha}{d}\theta\:=\:\rho{gdx} \\ $$$${using}\:\left({iii}\right) \\ $$$$\:\:\:\:\:\:\:\frac{\rho{g}\left(\frac{{l}}{\mathrm{2}}\right)\mathrm{cos}\:\alpha}{\mathrm{cos}\:\theta.\mathrm{sin}\:\alpha}{d}\theta\:=\:\rho{gdx} \\ $$$$\:\:\:\:\frac{{l}}{\mathrm{2}}\frac{\mathrm{cos}\:\alpha}{\mathrm{sin}\:\alpha}\int_{\mathrm{0}} ^{\:\:\theta} \mathrm{sec}\:\theta\:=\:{x} \\ $$$$\Rightarrow\:\:{ln}\left(\mathrm{sec}\:\theta+\mathrm{tan}\:\theta\right)=\:\frac{\mathrm{2}{x}\mathrm{tan}\:\alpha}{{l}} \\ $$$$\:\:\:\:\sqrt{\mathrm{1}+\left(\frac{{dy}}{{dx}}\right)^{\mathrm{2}} }+\frac{{dy}}{{dx}}\:=\:{e}^{\frac{\mathrm{2}{x}\mathrm{tan}\:\alpha}{{l}}} \\ $$$${squaring} \\ $$$$\:\:\:\:\:\:\mathrm{1}=\:{e}^{\frac{\mathrm{4}{x}\mathrm{tan}\:\alpha}{{l}}} −\mathrm{2}\left(\frac{{dy}}{{dx}}\right){e}^{\frac{\mathrm{2}{x}\mathrm{tan}\:\alpha}{{l}}} \\ $$$$\Rightarrow\:\:\frac{{dy}}{{dx}}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\left({e}^{\frac{\mathrm{2}{x}\mathrm{tan}\:\alpha}{{l}}} −{e}^{−\frac{\mathrm{2}{x}\mathrm{tan}\:\alpha}{{l}}} \right) \\ $$$${and}\:{this}\:{at}\:{B}\:\left({x}=\frac{{b}}{\mathrm{2}}\right),\:{gives}\:\:\: \\ $$$$\:\:\:\:\:\:\:\mathrm{2tan}\:\alpha\:=\:{e}^{\frac{{b}\mathrm{tan}\:\alpha}{{l}}} −{e}^{−\frac{{b}\mathrm{tan}\:\alpha}{{l}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}{m}=\:{t}−\frac{\mathrm{1}}{{t}}\:\:\:\:\:\:\:\:\:\left({say}\right) \\ $$$$\Rightarrow\:\:\:\:{t}^{\mathrm{2}} −\mathrm{2}{mt}\:−\mathrm{1}\:=\:\mathrm{0} \\ $$$${or}\:\:\:\:\:\left({t}−{m}\right)^{\mathrm{2}} =\:\mathrm{1}+{m}^{\mathrm{2}} \\ $$$$\:\:\:{t}\:=\:{e}^{\frac{{bm}}{{l}}} \:=\:{m}+\sqrt{\mathrm{1}+{m}^{\mathrm{2}} } \\ $$$$\Rightarrow\:\:\frac{{b}\mathrm{tan}\:\alpha}{{l}}\:=\:{ln}\left(\:\mathrm{tan}\:\alpha+\mathrm{sec}\:\alpha\right)\:\:\:…\left({I}\right) \\ $$$$\:\:\:{further}\:\:\:\boldsymbol{{T}}_{{B}} \:=\:\boldsymbol{\rho{gz}}\:=\:\frac{\boldsymbol{\rho{gl}}}{\mathrm{2sin}\:\boldsymbol{\alpha}} \\ $$$$\:\:\:{or}\:\:\:\:\:{z}\:=\:\frac{{l}}{\mathrm{2sin}\:\alpha} \\ $$$$\left({z}\:{being}\:{the}\:{vertically}\:{hanging}\:{length}\right) \\ $$$$\:\:\:\:{L}\:=\:{l}+{z}\:=\:{l}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2sin}\:\alpha}\right) \\ $$$${and}\:{from}\:\left({I}\right)\:\left(\mathrm{4}\:{lines}\:{above}\right) \\ $$$$\:\:\:{L}\:=\:\frac{{b}\mathrm{tan}\:\alpha}{{ln}\left(\mathrm{tan}\:\alpha+\mathrm{sec}\:\alpha\right)}\left(\frac{\mathrm{2sin}\:\alpha+\mathrm{1}}{\mathrm{2sin}\:\alpha}\right) \\ $$$$\:\:\:\:\:{L}\:=\:\frac{{b}\left(\mathrm{2sin}\:\alpha+\mathrm{1}\right)}{\mathrm{2cos}\:\alpha\:{ln}\left(\mathrm{tan}\:\alpha+\mathrm{sec}\:\alpha\right)}\:\:…\left({A}\right) \\ $$$$\Rightarrow\:\frac{{b}}{\mathrm{2}{L}}\:=\:\frac{\mathrm{cos}\:\alpha\:{ln}\left(\mathrm{tan}\:\alpha+\mathrm{sec}\:\alpha\right)}{\left(\mathrm{2sin}\:\alpha+\mathrm{1}\right)} \\ $$$$\:\frac{{d}}{{d}\alpha}\left(\frac{{b}}{\mathrm{2}{L}}\right)\:=\:\mathrm{0}\:\:\:\Rightarrow \\ $$$$\:\:\:\frac{\mathrm{cos}\:\alpha}{\left(\mathrm{2sin}\:\alpha+\mathrm{1}\right)}×\mathrm{sec}\:\alpha\: \\ $$$$\:\:\:+\frac{\left(\mathrm{2sin}\:\alpha+\mathrm{1}\right)\left(−\mathrm{sin}\:\alpha\right)−\mathrm{2cos}\:^{\mathrm{2}} \alpha}{\left(\mathrm{2sin}\:\alpha+\mathrm{1}\right)^{\mathrm{2}} }\:{ln}\left(\mathrm{tan}\:\alpha+\mathrm{sec}\:\alpha\right)=\:\mathrm{0} \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$$\Rightarrow\:{ln}\left(\mathrm{sec}\:\alpha+\mathrm{tan}\:\alpha\right)=\:\frac{\mathrm{2sin}\:\alpha+\mathrm{1}}{\mathrm{2}+\mathrm{sin}\:\alpha}\:\:..\left({B}\right) \\ $$$$\:\:\:\Rightarrow\:\left\{\:\alpha\:=\:\mathrm{45}.\mathrm{5274}°\:\:\:\right\} \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$${utilizing}\:{this}\:{in}\:\left({A}\right) \\ $$$$\:\:\:{L}\:=\:\frac{{b}\left(\mathrm{2sin}\:\alpha+\mathrm{1}\right)}{\mathrm{2cos}\:\alpha}×\frac{\left(\mathrm{2}+\mathrm{sin}\:\alpha\right)}{\left(\mathrm{2sin}\:\alpha+\mathrm{1}\right)} \\ $$$$\Rightarrow\:\:\boldsymbol{{L}}\:=\:\frac{{b}\left(\mathrm{2}+\mathrm{sin}\:\alpha\right)}{\mathrm{2cos}\:\alpha}\:=\:\mathrm{1}.\mathrm{9367}\boldsymbol{{b}}\:. \\ $$
Commented by mr W last updated on 30/Dec/18
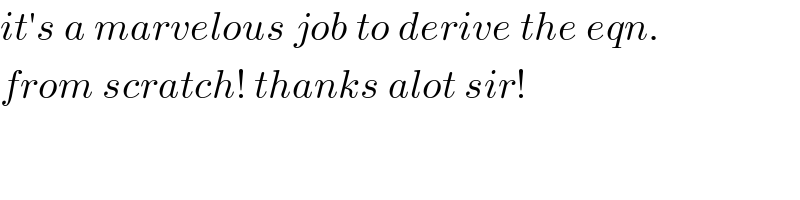
it′s a marvelous job to derive the eqn. from scratch! thanks alot sir!
$${it}'{s}\:{a}\:{marvelous}\:{job}\:{to}\:{derive}\:{the}\:{eqn}. \\ $$$${from}\:{scratch}!\:{thanks}\:{alot}\:{sir}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *