Question Number 51712 by ajfour last updated on 29/Dec/18
Commented by ajfour last updated on 29/Dec/18
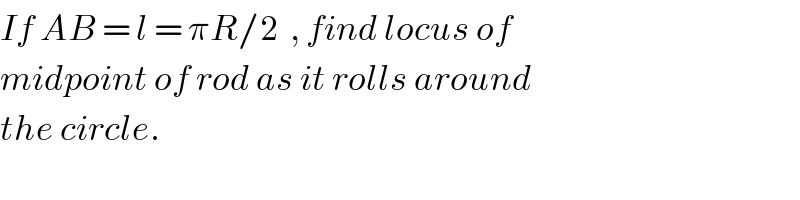
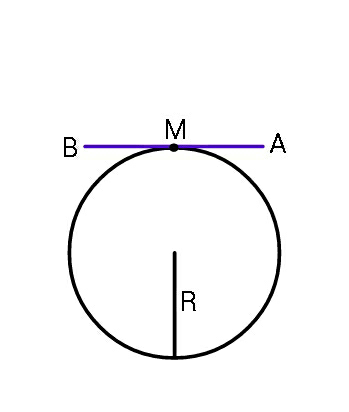
$${If}\:{AB}\:=\:{l}\:=\:\pi{R}/\mathrm{2}\:\:,\:{find}\:{locus}\:{of} \\ $$$${midpoint}\:{of}\:{rod}\:{as}\:{it}\:{rolls}\:{around} \\ $$$${the}\:{circle}. \\ $$
Commented by mr W last updated on 29/Dec/18
Commented by mr W last updated on 29/Dec/18
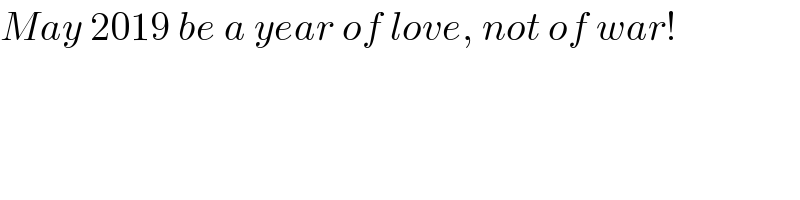
$${May}\:\mathrm{2019}\:{be}\:{a}\:{year}\:{of}\:{love},\:{not}\:{of}\:{war}! \\ $$
Commented by Abdo msup. last updated on 29/Dec/18

$${thank}\:{you}\:{sir}\:{and}\:\:{happy}\:{new}\:{year}\:{to}\:{all}\:{person} \\ $$$${actifs}\:{in}\:{this}\:{plateform}…. \\ $$
Commented by ajfour last updated on 30/Dec/18

$${So}\:{be}\:{it},\:{but}\:{this}\:{point}\:{A}\:{in}\:{question} \\ $$$${shall}\:{stagnate}\:{after}\:{it}\:{becomes}\:{point} \\ $$$${of}\:{tangency},\:{A}\:{will}\:{be}\:{centre}\:{of} \\ $$$${circlular}\:{locus}\:{of}\:{M}\:{about}\:{A},\:{till} \\ $$$${rod}\:{turns}\:{by}\:\mathrm{180}°\:;\:{only}\:{thereafter} \\ $$$${shall}\:{A}\:{rise}\:{from}\:{circumference} \\ $$$${of}\:{given}\:{circle},\:{dear}\:{Sir};\:{shouldn}'{t} \\ $$$${it}\:{be}\:{so}\:? \\ $$
Commented by ajfour last updated on 30/Dec/18
Commented by mr W last updated on 30/Dec/18

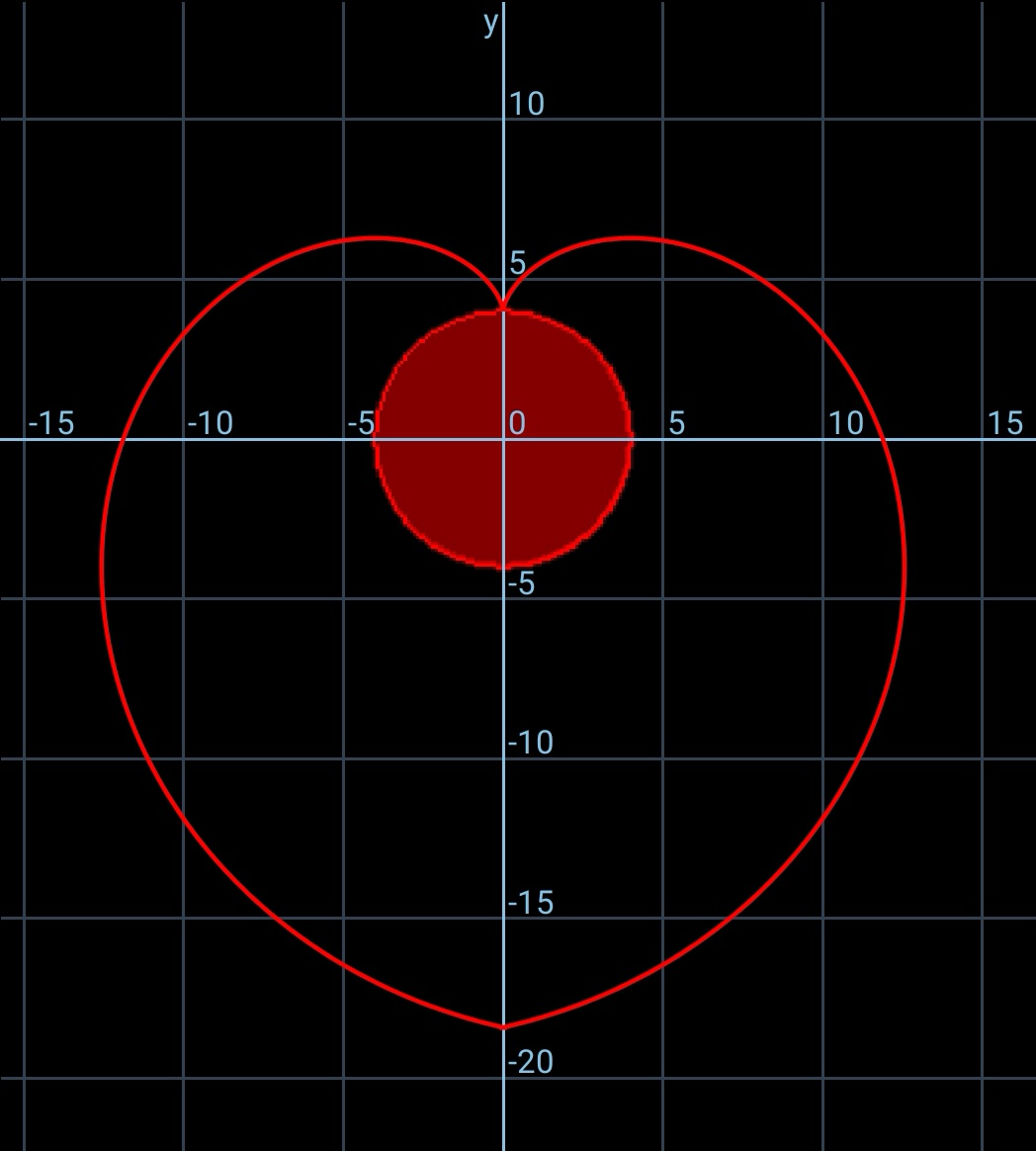
$${ajfour}\:{sir}:\:{you}'{re}\:{basically}\:{right}.\: \\ $$$${the}\:{shape}\:{of}\:{locus}\:{M}\:{depends}\:{very}\:{much} \\ $$$${on}\:{how}\:{long}\:{the}\:{rod}\:{is}. \\ $$$${i}\:{just}\:{have}\:{made}\:{the}\:{rod}\:{a}\:{little}\:{bit} \\ $$$${longer}\:{such}\:{that}\:{the}\:{locus}\:{of}\:{M}\:{becomes} \\ $$$${the}\:{shape}\:{of}\:{a}\:{beautiful}\:{heart}.\:{to}\:{be} \\ $$$${exact},\:{my}\:{rod}\:{has}\:{a}\:{length}\:{of}\:\mathrm{9}{R}.\:{it} \\ $$$${can}\:{rotate}\:{both}\:{clockwise}\:{and}\:{anti}− \\ $$$${clockwise}. \\ $$
Commented by mr W last updated on 30/Dec/18
Commented by mr W last updated on 30/Dec/18

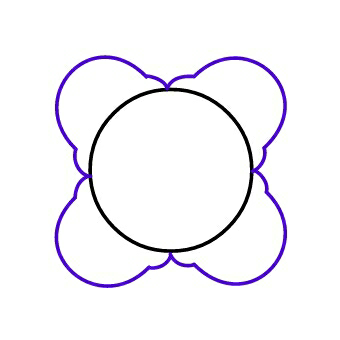
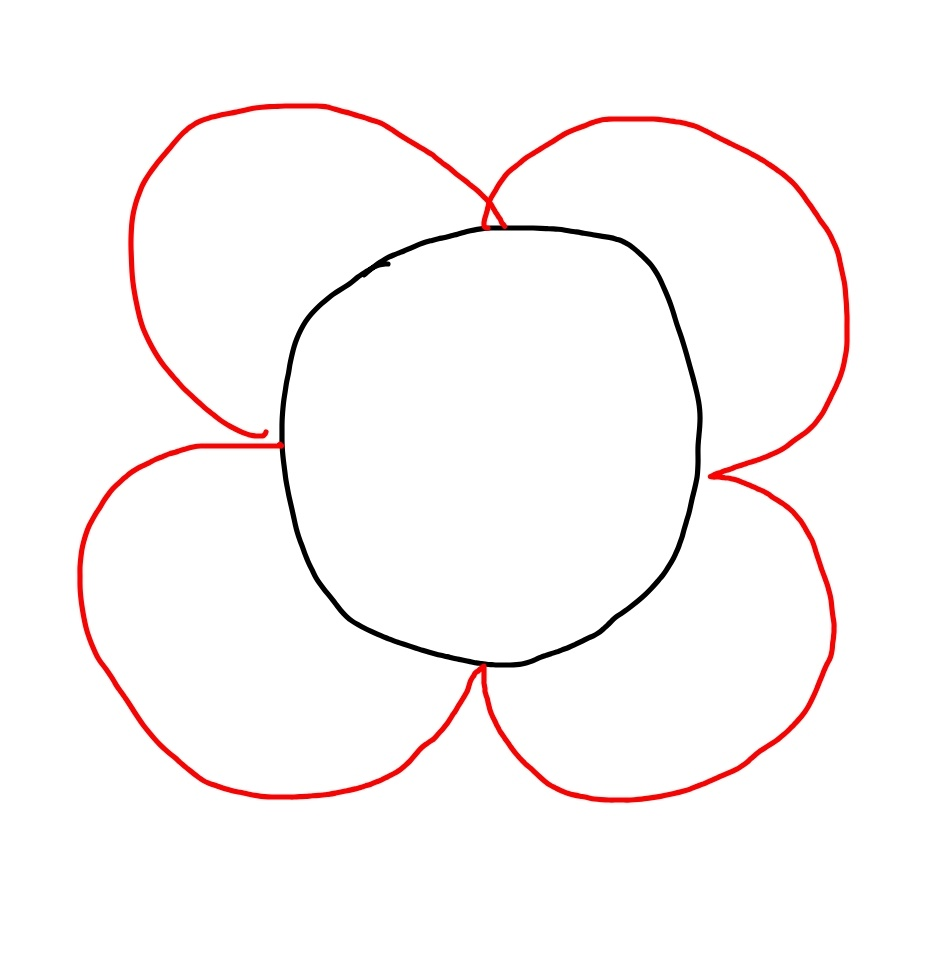
$${to}\:{be}\:{exact},\:{the}\:{locus}\:{of}\:{M}\:{with}\:{rod} \\ $$$${length}\:{given}\:{in}\:{question}\:{should}\:{look} \\ $$$${like}\:{this}.\:{the}\:{parts}\:{of}\:{the}\:{locus}\:{curve} \\ $$$${are}\:{jointed}\:{smoothly}\:{to}\:{each}\:{other}. \\ $$
