Question Number 51805 by azizullah last updated on 30/Dec/18
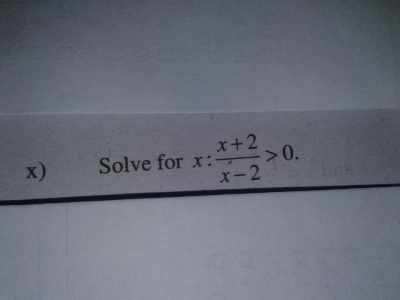
Commented by tanmay.chaudhury50@gmail.com last updated on 30/Dec/18
Commented by maxmathsup by imad last updated on 30/Dec/18
![the inequation is defined on R−{2} and (e) ⇔(((x+2)(x−2))/((x−2)^2 ))>0 ⇔ (x+2)(x−2)>0 and x≠2 ⇔ x ∈]−∞,−2[∪]2,+∞[.](https://www.tinkutara.com/question/Q51814.png)
$${the}\:{inequation}\:{is}\:{defined}\:{on}\:{R}−\left\{\mathrm{2}\right\}\:\:{and}\:\left({e}\right)\:\Leftrightarrow\frac{\left({x}+\mathrm{2}\right)\left({x}−\mathrm{2}\right)}{\left({x}−\mathrm{2}\right)^{\mathrm{2}} }>\mathrm{0}\:\Leftrightarrow \\ $$$$\left.\left({x}+\mathrm{2}\right)\left({x}−\mathrm{2}\right)>\mathrm{0}\:{and}\:{x}\neq\mathrm{2}\:\Leftrightarrow\:{x}\:\in\right]−\infty,−\mathrm{2}\left[\cup\right]\mathrm{2},+\infty\left[.\right. \\ $$
Commented by azizullah last updated on 31/Dec/18
$$\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{thanks}}\:\boldsymbol{\mathrm{so}}\:\boldsymbol{\mathrm{much}}\:\boldsymbol{\mathrm{dear}}\:\boldsymbol{\mathrm{sir}}. \\ $$
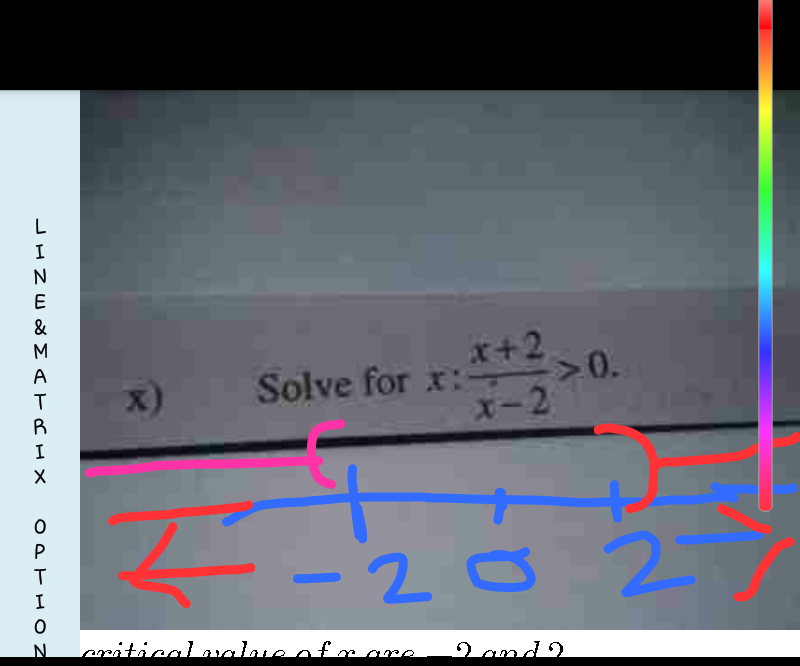
Answered by tanmay.chaudhury50@gmail.com last updated on 30/Dec/18
![critical value of x are −2 and 2 1)x≠2 because at x=2 D_r =0 2)when x>2 N_r >0 and D_r >0 (N_r /D_(r ) )>0 [given condition ((x+2)/(x−2))>0 fulfill] 3)2>x>−2 [say x=1 then N_r >0 D_r <0 (N_r /D_r )<0 so given condition ((x+2)/(x−2))>0 does not fulfill 3)x<−2 [say x=−3 N_r =−ve D_r =−ve but (N_r /D_r )>0 given condition ((x+2)/(x−2))>0 fullfill 4)x=−2 N_r =0 D_r =−4 (N_r /D_r )=0 but given condition does not fulfill ((x+2)/(x−2))>0 so solution set is (−∞,−2)∪(2,+∞)](https://www.tinkutara.com/question/Q51808.png)
$${critical}\:{value}\:{of}\:{x}\:{are}\:−\mathrm{2}\:{and}\:\mathrm{2} \\ $$$$\left.\mathrm{1}\right){x}\neq\mathrm{2}\:\:{because}\:{at}\:{x}=\mathrm{2}\:{D}_{{r}} =\mathrm{0} \\ $$$$\left.\mathrm{2}\right){when}\:{x}>\mathrm{2}\:\:\:{N}_{{r}} >\mathrm{0}\:\:{and}\:\:{D}_{{r}} >\mathrm{0} \\ $$$$\:\:\:\frac{{N}_{{r}} }{{D}_{{r}\:} }>\mathrm{0}\:\:\:\:\left[{given}\:{condition}\:\frac{{x}+\mathrm{2}}{{x}−\mathrm{2}}>\mathrm{0}\:{fulfill}\right] \\ $$$$\left.\mathrm{3}\right)\mathrm{2}>{x}>−\mathrm{2}\:\:\left[{say}\:{x}=\mathrm{1}\:\:{then}\:{N}_{{r}} >\mathrm{0}\:\:{D}_{{r}} <\mathrm{0}\:\:\:\frac{{N}_{{r}} }{{D}_{{r}} }<\mathrm{0}\right. \\ $$$$\:{so}\:{given}\:{condition}\:\frac{{x}+\mathrm{2}}{{x}−\mathrm{2}}>\mathrm{0}\:{does}\:{not}\:{fulfill} \\ $$$$\left.\mathrm{3}\right){x}<−\mathrm{2}\:\:\left[{say}\:{x}=−\mathrm{3}\:\:\:{N}_{{r}} =−{ve}\:\:{D}_{{r}} =−{ve}\:{but}\right. \\ $$$$\:\:\:\frac{{N}_{{r}} }{{D}_{{r}} }>\mathrm{0}\:\:{given}\:{condition}\:\:\frac{{x}+\mathrm{2}}{{x}−\mathrm{2}}>\mathrm{0}\:{fullfill} \\ $$$$ \\ $$$$\left.\mathrm{4}\right){x}=−\mathrm{2}\:\:\:{N}_{{r}} =\mathrm{0}\:\:\:{D}_{{r}} =−\mathrm{4}\:\:\:\frac{{N}_{{r}} }{{D}_{{r}} }=\mathrm{0} \\ $$$${but}\:{given}\:{condition}\:{does}\:{not}\:{fulfill}\: \\ $$$$\:\:\frac{{x}+\mathrm{2}}{{x}−\mathrm{2}}>\mathrm{0} \\ $$$${so}\:{solution}\:{set}\:{is}\: \\ $$$$\left(−\infty,−\mathrm{2}\right)\cup\left(\mathrm{2},+\infty\right) \\ $$$$ \\ $$
Commented by azizullah last updated on 31/Dec/18

$$\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{thanks}}\:\boldsymbol{\mathrm{dear}}\:\boldsymbol{\mathrm{sir}}. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 31/Dec/18

$${most}\:{welcome}… \\ $$
Answered by afachri last updated on 30/Dec/18

$$\:\:\:“\:>\:\mathrm{0}\:''\:\mathrm{means}\:\mathrm{always}\:\mathrm{possitive}.\:\mathrm{It}\:\mathrm{happen} \\ $$$$\:\:\:\:\mathrm{when}\:: \\ $$$$\:\:\:\:\frac{\mathrm{negative}}{\mathrm{negative}}\:\:\mathrm{or}\:\:\frac{\mathrm{possitive}}{\mathrm{possitive}} \\ $$$$ \\ $$$$\mathrm{when}\:\left({x}\:−\:\mathrm{2}\right)\:\mathrm{is}\:\mathrm{possitive},\:\left({x}\:+\:\mathrm{2}\right)\:\mathrm{also}\:\mathrm{possitive}. \\ $$$$\mathrm{it}\:\mathrm{happens}\:\mathrm{when}\:{x}\::\: \\ $$$$\:\:\:\:\:{x}\:−\:\mathrm{2}\:>\:\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:{x}\:\:\:\:\:>\:\:\:\mathrm{2} \\ $$$$\mathrm{when}\:\left({x}\:+\:\mathrm{2}\right)\:\mathrm{is}\:\mathrm{negative},\:\mathrm{so}\:\mathrm{is}\:\left({x}−\mathrm{2}\right). \\ $$$${x}\:+\:\mathrm{2}\:<\:\mathrm{0} \\ $$$$\:\:\:\:\:{x}\:\:\:\:\:\:<\:−\mathrm{2} \\ $$$$ \\ $$$$\mathrm{set}\:\mathrm{of}\:\mathrm{solution}\:\:\:\left\{\:−\mathrm{2}\:>\:{x}\:>\:\mathrm{2}\:,\:{x}\in\mathbb{R}\:\right\} \\ $$$$ \\ $$
Commented by azizullah last updated on 31/Dec/18

$$\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{thanks}}\:\boldsymbol{\mathrm{sir}}\:\boldsymbol{\mathrm{for}}\:\boldsymbol{\mathrm{solution}}\:\boldsymbol{\mathrm{of}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{given}}\:\boldsymbol{\mathrm{equation}}. \\ $$
Commented by afachri last updated on 31/Dec/18

$$\mathrm{you}'\mathrm{re}\:\mathrm{welcome}\:\mathrm{Azizullah} \\ $$
