Question Number 51849 by ajfour last updated on 31/Dec/18
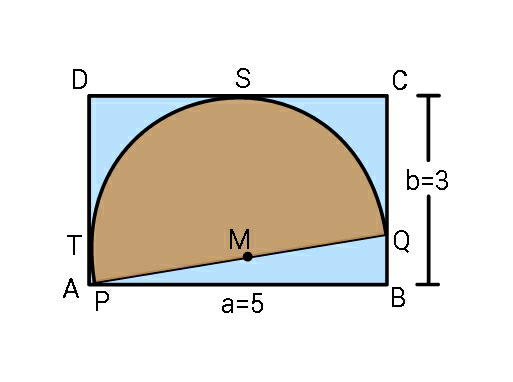
Commented by ajfour last updated on 31/Dec/18
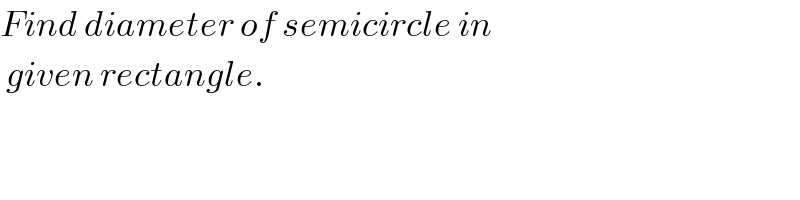
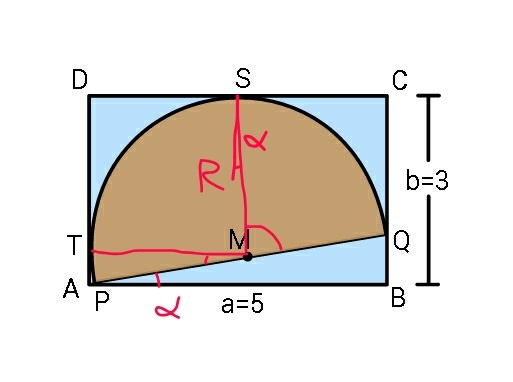
$${Find}\:{diameter}\:{of}\:{semicircle}\:{in} \\ $$$$\:{given}\:{rectangle}. \\ $$
Commented by mr W last updated on 31/Dec/18
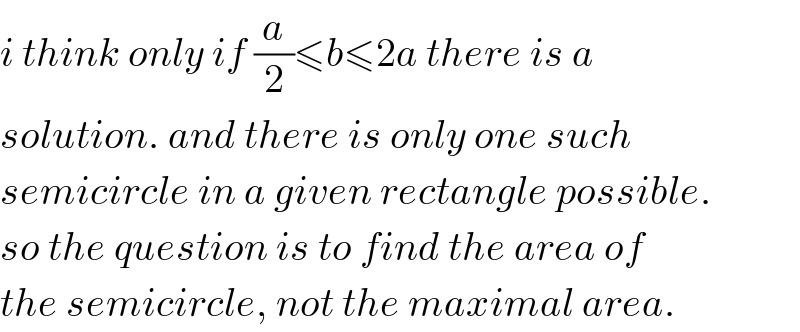
$${i}\:{think}\:{only}\:{if}\:\frac{{a}}{\mathrm{2}}\leqslant{b}\leqslant\mathrm{2}{a}\:{there}\:{is}\:{a} \\ $$$${solution}.\:{and}\:{there}\:{is}\:{only}\:{one}\:{such} \\ $$$${semicircle}\:{in}\:{a}\:{given}\:{rectangle}\:{possible}. \\ $$$${so}\:{the}\:{question}\:{is}\:{to}\:{find}\:{the}\:{area}\:{of} \\ $$$${the}\:{semicircle},\:{not}\:{the}\:{maximal}\:{area}. \\ $$
Commented by ajfour last updated on 31/Dec/18

$${yes}\:{Sir},\:{i}'{ve}\:{edited};\:{please}\:{attempt}. \\ $$
Answered by MJS last updated on 31/Dec/18
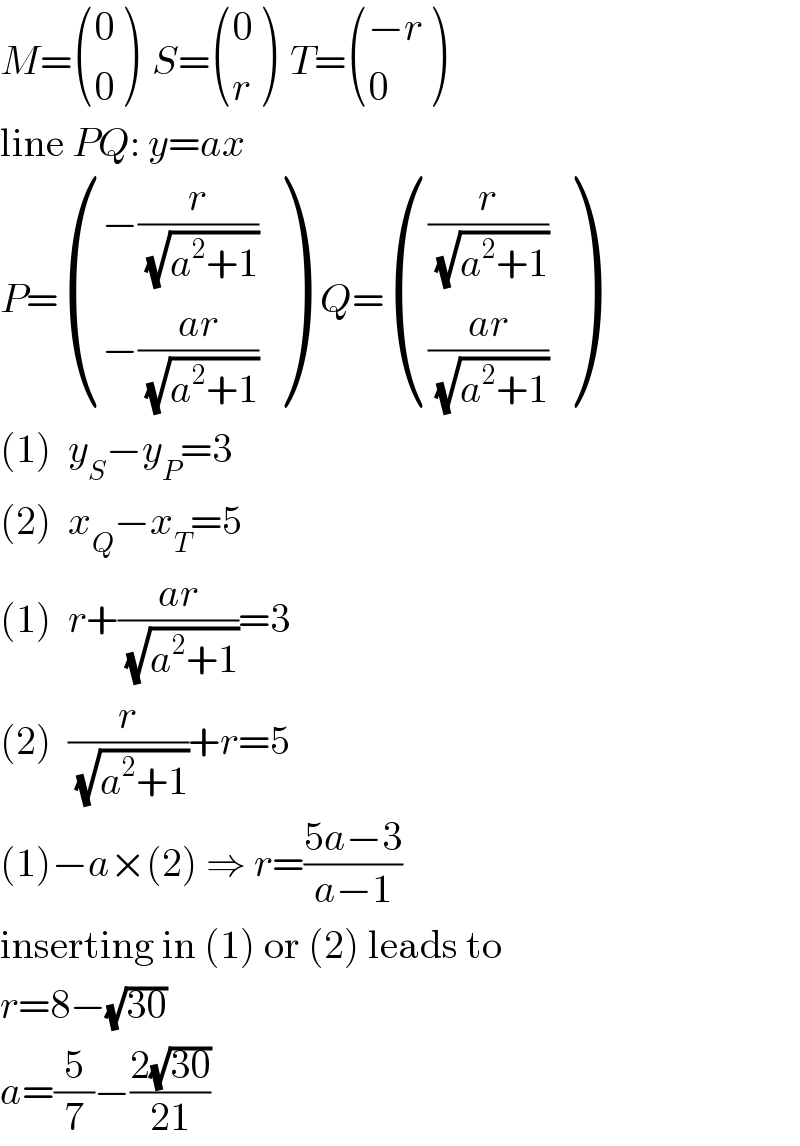
$${M}=\begin{pmatrix}{\mathrm{0}}\\{\mathrm{0}}\end{pmatrix}\:\:{S}=\begin{pmatrix}{\mathrm{0}}\\{{r}}\end{pmatrix}\:\:{T}=\begin{pmatrix}{−{r}}\\{\mathrm{0}}\end{pmatrix} \\ $$$$\mathrm{line}\:{PQ}:\:{y}={ax} \\ $$$${P}=\begin{pmatrix}{−\frac{{r}}{\:\sqrt{{a}^{\mathrm{2}} +\mathrm{1}}}}\\{−\frac{{ar}}{\:\sqrt{{a}^{\mathrm{2}} +\mathrm{1}}}}\end{pmatrix}\:\:{Q}=\begin{pmatrix}{\frac{{r}}{\:\sqrt{{a}^{\mathrm{2}} +\mathrm{1}}}}\\{\frac{{ar}}{\:\sqrt{{a}^{\mathrm{2}} +\mathrm{1}}}}\end{pmatrix} \\ $$$$\left(\mathrm{1}\right)\:\:{y}_{{S}} −{y}_{{P}} =\mathrm{3} \\ $$$$\left(\mathrm{2}\right)\:\:{x}_{{Q}} −{x}_{{T}} =\mathrm{5} \\ $$$$\left(\mathrm{1}\right)\:\:{r}+\frac{{ar}}{\:\sqrt{{a}^{\mathrm{2}} +\mathrm{1}}}=\mathrm{3} \\ $$$$\left(\mathrm{2}\right)\:\:\frac{{r}}{\:\sqrt{{a}^{\mathrm{2}} +\mathrm{1}}}+{r}=\mathrm{5} \\ $$$$\left(\mathrm{1}\right)−{a}×\left(\mathrm{2}\right)\:\Rightarrow\:{r}=\frac{\mathrm{5}{a}−\mathrm{3}}{{a}−\mathrm{1}} \\ $$$$\mathrm{inserting}\:\mathrm{in}\:\left(\mathrm{1}\right)\:\mathrm{or}\:\left(\mathrm{2}\right)\:\mathrm{leads}\:\mathrm{to} \\ $$$${r}=\mathrm{8}−\sqrt{\mathrm{30}} \\ $$$${a}=\frac{\mathrm{5}}{\mathrm{7}}−\frac{\mathrm{2}\sqrt{\mathrm{30}}}{\mathrm{21}} \\ $$
Commented by ajfour last updated on 31/Dec/18

$${Excellent}\:{Sir},\:{Thanks}\:{a}\:{lot}! \\ $$$$\mathcal{HAPPY}\:\:\mathcal{NEW}\:\mathcal{YEAR}\:! \\ $$
Commented by MJS last updated on 31/Dec/18
$$\mathrm{thank}\:\mathrm{you},\:\mathrm{and}\:\mathrm{all}\:\mathrm{the}\:\mathrm{best}\:\mathrm{for}\:\mathrm{you}\:\mathrm{too}! \\ $$
Answered by mr W last updated on 31/Dec/18
Commented by mr W last updated on 31/Dec/18
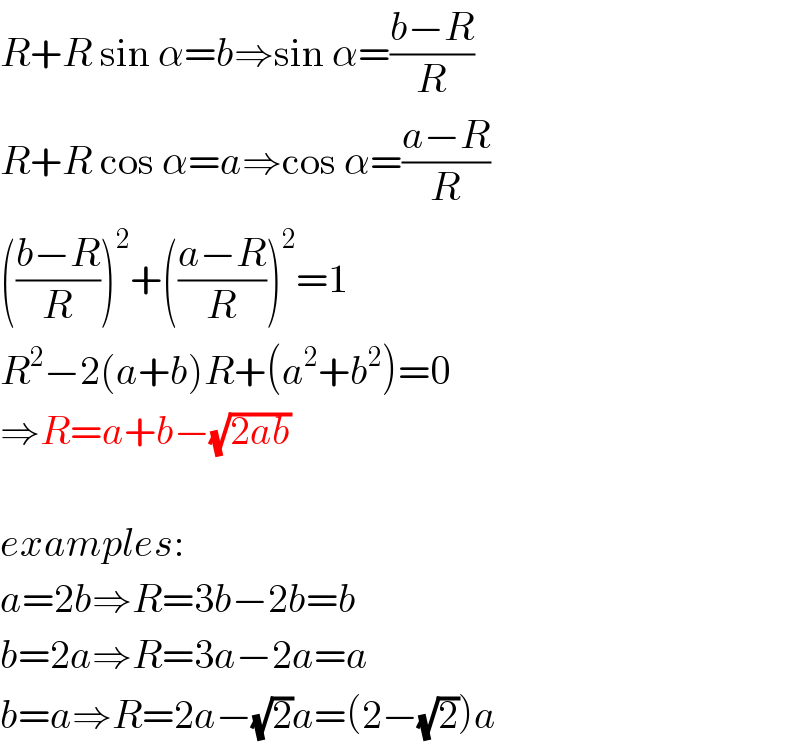
$${R}+{R}\:\mathrm{sin}\:\alpha={b}\Rightarrow\mathrm{sin}\:\alpha=\frac{{b}−{R}}{{R}} \\ $$$${R}+{R}\:\mathrm{cos}\:\alpha={a}\Rightarrow\mathrm{cos}\:\alpha=\frac{{a}−{R}}{{R}} \\ $$$$\left(\frac{{b}−{R}}{{R}}\right)^{\mathrm{2}} +\left(\frac{{a}−{R}}{{R}}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$${R}^{\mathrm{2}} −\mathrm{2}\left({a}+{b}\right){R}+\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\Rightarrow{R}={a}+{b}−\sqrt{\mathrm{2}{ab}} \\ $$$$ \\ $$$${examples}: \\ $$$${a}=\mathrm{2}{b}\Rightarrow{R}=\mathrm{3}{b}−\mathrm{2}{b}={b}\: \\ $$$${b}=\mathrm{2}{a}\Rightarrow{R}=\mathrm{3}{a}−\mathrm{2}{a}={a} \\ $$$${b}={a}\Rightarrow{R}=\mathrm{2}{a}−\sqrt{\mathrm{2}}{a}=\left(\mathrm{2}−\sqrt{\mathrm{2}}\right){a} \\ $$
Commented by ajfour last updated on 31/Dec/18

$${best}\:{way}\:{Sir}! \\ $$
Answered by ajfour last updated on 31/Dec/18

$${R}\:=\:{a}+{b}−\sqrt{\mathrm{2}{ab}}\:\:\:\:\:\left({I}\:{found}\right). \\ $$
