Question Number 51884 by ajfour last updated on 31/Dec/18

Commented by ajfour last updated on 31/Dec/18

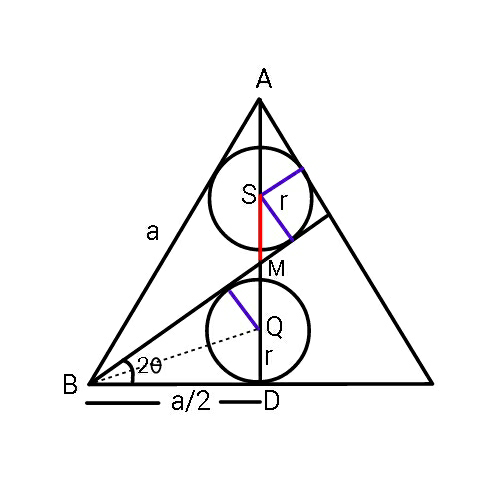
$${Relate}\:{radius}\:\boldsymbol{{r}}\:{of}\:{the}\:{two}\:{circles} \\ $$$$\left({the}\:{same}\right)\:{with}\:{side}\:{length}\:\boldsymbol{{a}}\:{of} \\ $$$${the}\:{equilateral}\:{triangle}. \\ $$
Commented by mr W last updated on 01/Jan/19

$$\frac{{r}}{{a}}=\frac{\sqrt{\mathrm{3}}−\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$
Commented by ajfour last updated on 01/Jan/19
![AD = ((a(√3))/2) = AS+SM+MQ+QD ((a(√3))/2) = 2r+(r/(cos 2θ))+(r/(cos 2θ))+r tan θ = ((2r)/a) = t ((a(√3))/2) = 3r+((2r[1+(((2r)/a))^2 ])/([1−(((2r)/a))^2 ])) let (√3) = 3t+((2t(1+t^2 ))/(1−t^2 )) (√3)−(√3)t^2 = 3t−3t^3 +2t+2t^3 t^3 −(√3)t^2 −5t+(√3) = 0](https://www.tinkutara.com/question/Q51928.png)
$${AD}\:=\:\frac{{a}\sqrt{\mathrm{3}}}{\mathrm{2}}\:=\:{AS}+{SM}+{MQ}+{QD} \\ $$$$\frac{{a}\sqrt{\mathrm{3}}}{\mathrm{2}}\:=\:\mathrm{2}{r}+\frac{{r}}{\mathrm{cos}\:\mathrm{2}\theta}+\frac{{r}}{\mathrm{cos}\:\mathrm{2}\theta}+{r} \\ $$$$\:\:\mathrm{tan}\:\theta\:=\:\frac{\mathrm{2}{r}}{{a}}\:=\:{t} \\ $$$$\frac{{a}\sqrt{\mathrm{3}}}{\mathrm{2}}\:=\:\mathrm{3}{r}+\frac{\mathrm{2}{r}\left[\mathrm{1}+\left(\frac{\mathrm{2}{r}}{{a}}\right)^{\mathrm{2}} \right]}{\left[\mathrm{1}−\left(\frac{\mathrm{2}{r}}{{a}}\right)^{\mathrm{2}} \right]} \\ $$$${let}\: \\ $$$$\:\sqrt{\mathrm{3}}\:=\:\mathrm{3}{t}+\frac{\mathrm{2}{t}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}{\mathrm{1}−{t}^{\mathrm{2}} } \\ $$$$\sqrt{\mathrm{3}}−\sqrt{\mathrm{3}}{t}^{\mathrm{2}} =\:\mathrm{3}{t}−\mathrm{3}{t}^{\mathrm{3}} +\mathrm{2}{t}+\mathrm{2}{t}^{\mathrm{3}} \\ $$$${t}^{\mathrm{3}} −\sqrt{\mathrm{3}}{t}^{\mathrm{2}} −\mathrm{5}{t}+\sqrt{\mathrm{3}}\:=\:\mathrm{0} \\ $$
Commented by ajfour last updated on 01/Jan/19
Answered by mr W last updated on 01/Jan/19

$${let}\:\alpha=\angle{PBC} \\ $$$${BO}={CO}=\frac{{a}}{\mathrm{2}\:\mathrm{cos}\:\alpha} \\ $$$${DO}=\frac{{a}\:\mathrm{tan}\:\alpha}{\mathrm{2}} \\ $$$$\Delta_{{BOC}} =\frac{{a}}{\mathrm{2}}×\frac{{a}\:\mathrm{tan}\:\alpha}{\mathrm{2}}=\frac{{r}}{\mathrm{2}}\left({a}+\mathrm{2}×\frac{{a}}{\mathrm{2}\:\mathrm{cos}\:\alpha}\right) \\ $$$$\frac{{a}\:\mathrm{tan}\:\alpha}{\mathrm{2}}={r}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{cos}\:\alpha}\right) \\ $$$$\Rightarrow{r}=\frac{{a}\:\mathrm{sin}\:\alpha}{\mathrm{2}\left(\mathrm{1}+\mathrm{cos}\:\alpha\right)}=\frac{{a}}{\mathrm{2}}\:\mathrm{tan}\:\frac{\alpha}{\mathrm{2}}\:…\left({i}\right) \\ $$$${BR}=\frac{{a}\:\mathrm{sin}\:\alpha}{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}+\alpha\right)} \\ $$$${AR}={a}−\frac{{a}\:\mathrm{sin}\:\alpha}{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}+\alpha\right)}=\frac{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}+\alpha\right)−\mathrm{sin}\:\alpha}{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}+\alpha\right)}×{a} \\ $$$$=\frac{\sqrt{\mathrm{3}}\:\mathrm{cos}\:\alpha−\mathrm{sin}\:\alpha}{\:\sqrt{\mathrm{3}}\:\mathrm{cos}\:\alpha+\mathrm{sin}\:\alpha}×{a} \\ $$$${CR}=\frac{{a}\:\mathrm{sin}\:\frac{\pi}{\mathrm{3}}}{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}+\alpha\right)}=\frac{\sqrt{\mathrm{3}}\:{a}}{\:\sqrt{\mathrm{3}}\:\mathrm{cos}\:\alpha+\mathrm{sin}\:\alpha} \\ $$$$\Delta_{{ARC}} =\frac{{a}\:\mathrm{sin}\:\frac{\pi}{\mathrm{3}}}{\mathrm{2}}×\frac{\sqrt{\mathrm{3}}\:\mathrm{cos}\:\alpha−\mathrm{sin}\:\alpha}{\:\sqrt{\mathrm{3}}\:\mathrm{cos}\:\alpha+\mathrm{sin}\:\alpha}×{a}=\frac{{r}}{\mathrm{2}}\left({a}+\frac{\sqrt{\mathrm{3}}\:\mathrm{cos}\:\alpha−\mathrm{sin}\:\alpha}{\:\sqrt{\mathrm{3}}\:\mathrm{cos}\:\alpha+\mathrm{sin}\:\alpha}×{a}+\frac{\sqrt{\mathrm{3}}\:{a}}{\:\sqrt{\mathrm{3}}\:\mathrm{cos}\:\alpha+\mathrm{sin}\:\alpha}\right) \\ $$$$\Rightarrow{r}=\frac{\sqrt{\mathrm{3}}\:\mathrm{cos}\:\alpha−\mathrm{sin}\:\alpha}{\mathrm{2}\left(\mathrm{1}+\mathrm{2}\:\mathrm{cos}\:\alpha\right)}×{a}\:\:\:…\left({ii}\right) \\ $$$$\Rightarrow\frac{\mathrm{sin}\:\alpha}{\mathrm{1}+\mathrm{cos}\:\alpha}=\frac{\sqrt{\mathrm{3}}\:\mathrm{cos}\:\alpha−\mathrm{sin}\:\alpha}{\mathrm{1}+\mathrm{2}\:\mathrm{cos}\:\alpha} \\ $$$$\Rightarrow\mathrm{2}\:\mathrm{tan}\:\alpha+\mathrm{3}\:\mathrm{sin}\:\alpha=\sqrt{\mathrm{3}}\left(\mathrm{1}+\mathrm{cos}\:\alpha\right) \\ $$$${with}\:{t}=\mathrm{tan}\:\frac{\alpha}{\mathrm{2}} \\ $$$$\Rightarrow{t}^{\mathrm{3}} −\sqrt{\mathrm{3}}{t}^{\mathrm{2}} −\mathrm{5}{t}+\sqrt{\mathrm{3}}=\mathrm{0} \\ $$$$\Rightarrow{t}=\sqrt{\mathrm{3}}−\sqrt{\mathrm{2}} \\ $$$$\Rightarrow\frac{{r}}{{a}}=\frac{{t}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}−\sqrt{\mathrm{2}}}{\mathrm{2}}\:\approx\mathrm{0}.\mathrm{1589} \\ $$
Commented by ajfour last updated on 01/Jan/19

$${Thank}\:{you}\:{Sir}. \\ $$
