Question-51910

Question Number 51910 by Meritguide1234 last updated on 01/Jan/19

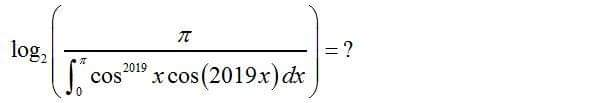
Commented by Abdo msup. last updated on 01/Jan/19

let find firstI_n = ∫_0 ^π cos^n x cos(nx)dx with n from N I_n =Re( ∫_0 ^π cos^n x e^(inx) dx) and ∫_0 ^π cos^n x e^(inx) dx =∫_0 ^π (((e^(ix) +e^(−ix) )/2))^n e^(inx) dx =(1/2^n ) ∫_0 ^π (Σ_(k=0) ^n C_n ^k e^(ikx) (e^(−i(n−k)x) )e^(inx) dx =(1/2^n ) ∫_0 ^π (Σ_(k=0) ^n C_n ^k e^(i2kx) )dx =(1/2^n ) Σ_(k=0) ^n ∫_0 ^π e^(2ikx) dx =(1/2^n )(π +Σ_(k=1) ^n [(1/(2ik)) e^(2ikx) ]_0 ^π ) =(π/2^n ) ⇒(π/I_n ) = 2^n ⇒log_2 ((π/I_n ))=n ⇒ log_2 ( (π/(∫_0 ^π cos^(2019) xcos(2019)xdx)))=2019 .

$${let}\:{find}\:{firstI}_{{n}} =\:\int_{\mathrm{0}} ^{\pi} \:{cos}^{{n}} {x}\:{cos}\left({nx}\right){dx}\:{with}\:{n}\:{from}\:{N} \\ $$$${I}_{{n}} ={Re}\left(\:\int_{\mathrm{0}} ^{\pi} \:{cos}^{{n}} {x}\:{e}^{{inx}} {dx}\right)\:{and} \\ $$$$\int_{\mathrm{0}} ^{\pi} \:{cos}^{{n}} {x}\:{e}^{{inx}} {dx}\:=\int_{\mathrm{0}} ^{\pi} \:\left(\frac{{e}^{{ix}} \:+{e}^{−{ix}} }{\mathrm{2}}\right)^{{n}} \:{e}^{{inx}} {dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\:\int_{\mathrm{0}} ^{\pi} \:\:\left(\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:\:{e}^{{ikx}} \:\:\left({e}^{−{i}\left({n}−{k}\right){x}} \right){e}^{{inx}} {dx}\right. \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\:\int_{\mathrm{0}} ^{\pi} \left(\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:\:{e}^{{i}\mathrm{2}{kx}} \right){dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\:\sum_{{k}=\mathrm{0}} ^{{n}} \:\int_{\mathrm{0}} ^{\pi} \:\:\:{e}^{\mathrm{2}{ikx}} {dx}\:=\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\left(\pi\:+\sum_{{k}=\mathrm{1}} ^{{n}} \left[\frac{\mathrm{1}}{\mathrm{2}{ik}}\:{e}^{\mathrm{2}{ikx}} \right]_{\mathrm{0}} ^{\pi} \right) \\ $$$$=\frac{\pi}{\mathrm{2}^{{n}} }\:\Rightarrow\frac{\pi}{{I}_{{n}} }\:=\:\mathrm{2}^{{n}} \:\:\:\Rightarrow{log}_{\mathrm{2}} \left(\frac{\pi}{{I}_{{n}} }\right)={n}\:\Rightarrow \\ $$$${log}_{\mathrm{2}} \left(\:\:\frac{\pi}{\int_{\mathrm{0}} ^{\pi} {cos}^{\mathrm{2019}} {xcos}\left(\mathrm{2019}\right){xdx}}\right)=\mathrm{2019}\:. \\ $$

Commented by tanmay.chaudhury50@gmail.com last updated on 01/Jan/19