Menu Close

Question-52061

Tinku Tara 0 Comments
Pin




Question Number 52061 by ajfour last updated on 02/Jan/19
Commented by ajfour last updated on 02/Jan/19
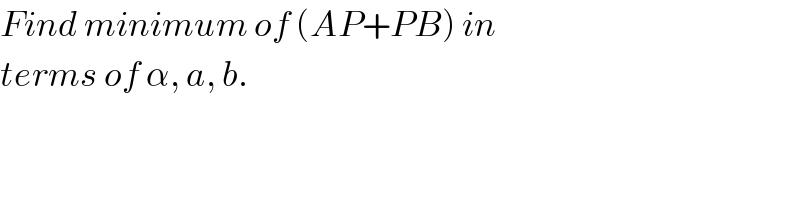
Find minimum of (AP+PB) in terms of α, a, b.
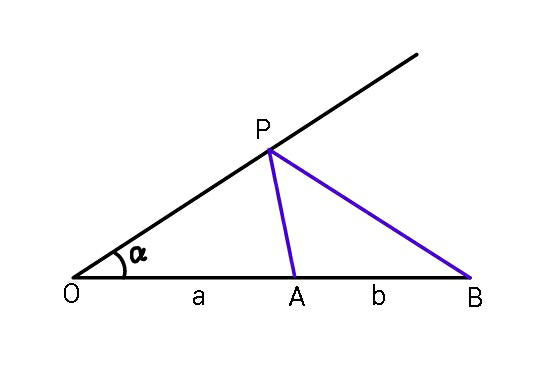
$${Find}\:{minimum}\:{of}\:\left({AP}+{PB}\right)\:{in} \\ $$$${terms}\:{of}\:\alpha,\:{a},\:{b}. \\ $$
Commented by MJS last updated on 14/Jan/19
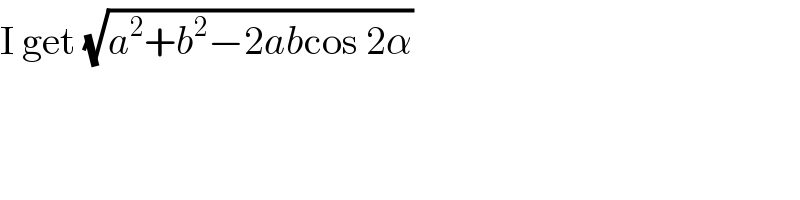
I get (√(a^2 +b^2 −2abcos 2α))
$$\mathrm{I}\:\mathrm{get}\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{ab}\mathrm{cos}\:\mathrm{2}\alpha} \\ $$
Commented by mr W last updated on 15/Jan/19
please recheck your solution sir. this result is not correct. example: b=0 min. path is obviously 2a sin α. according to your result it is a. according to my result it is (√(a^2 +a^2 −2a^2 cos 2α))=a(√(2(1−cos 2α))) =a(√(2×2 sin^2 α))=2a sin α. that means my result is correct.
$${please}\:{recheck}\:{your}\:{solution}\:{sir}. \\ $$$${this}\:{result}\:{is}\:{not}\:{correct}. \\ $$$$ \\ $$$${example}:\:{b}=\mathrm{0} \\ $$$${min}.\:{path}\:{is}\:{obviously}\:\mathrm{2}{a}\:\mathrm{sin}\:\alpha. \\ $$$$ \\ $$$${according}\:{to}\:{your}\:{result}\:{it}\:{is}\:{a}.\: \\ $$$$ \\ $$$${according}\:{to}\:{my}\:{result}\:{it}\:{is} \\ $$$$\sqrt{{a}^{\mathrm{2}} +{a}^{\mathrm{2}} −\mathrm{2}{a}^{\mathrm{2}} \mathrm{cos}\:\mathrm{2}\alpha}={a}\sqrt{\mathrm{2}\left(\mathrm{1}−\mathrm{cos}\:\mathrm{2}\alpha\right)} \\ $$$$={a}\sqrt{\mathrm{2}×\mathrm{2}\:\mathrm{sin}^{\mathrm{2}} \:\alpha}=\mathrm{2}{a}\:\mathrm{sin}\:\alpha.\:{that}\:{means} \\ $$$${my}\:{result}\:{is}\:{correct}. \\ $$
Answered by mr W last updated on 02/Jan/19
Commented by mr W last updated on 02/Jan/19
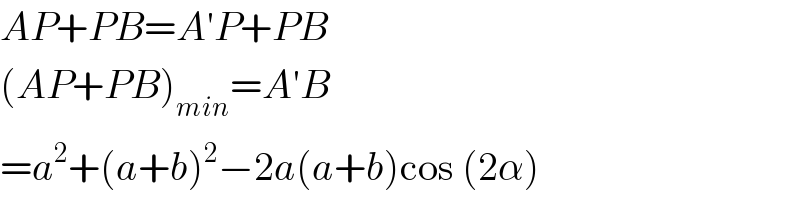
AP+PB=A′P+PB (AP+PB)_(min) =A′B =a^2 +(a+b)^2 −2a(a+b)cos (2α)
$${AP}+{PB}={A}'{P}+{PB} \\ $$$$\left({AP}+{PB}\right)_{{min}} ={A}'{B} \\ $$$$={a}^{\mathrm{2}} +\left({a}+{b}\right)^{\mathrm{2}} −\mathrm{2}{a}\left({a}+{b}\right)\mathrm{cos}\:\left(\mathrm{2}\alpha\right) \\ $$
Commented by ajfour last updated on 15/Jan/19
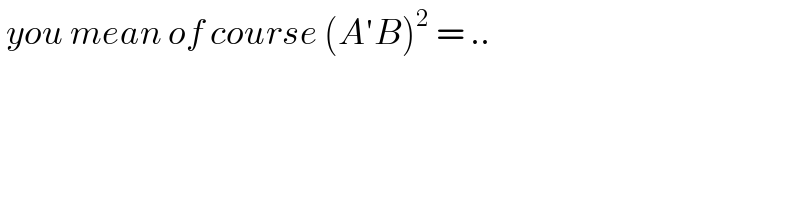
you mean of course (A′B)^2 = ..
$$\:{you}\:{mean}\:{of}\:{course}\:\left({A}'{B}\right)^{\mathrm{2}} \:=\:..\:\:\:\: \\ $$
Commented by mr W last updated on 15/Jan/19
yes sir.
$${yes}\:{sir}. \\ $$
Answered by MJS last updated on 15/Jan/19
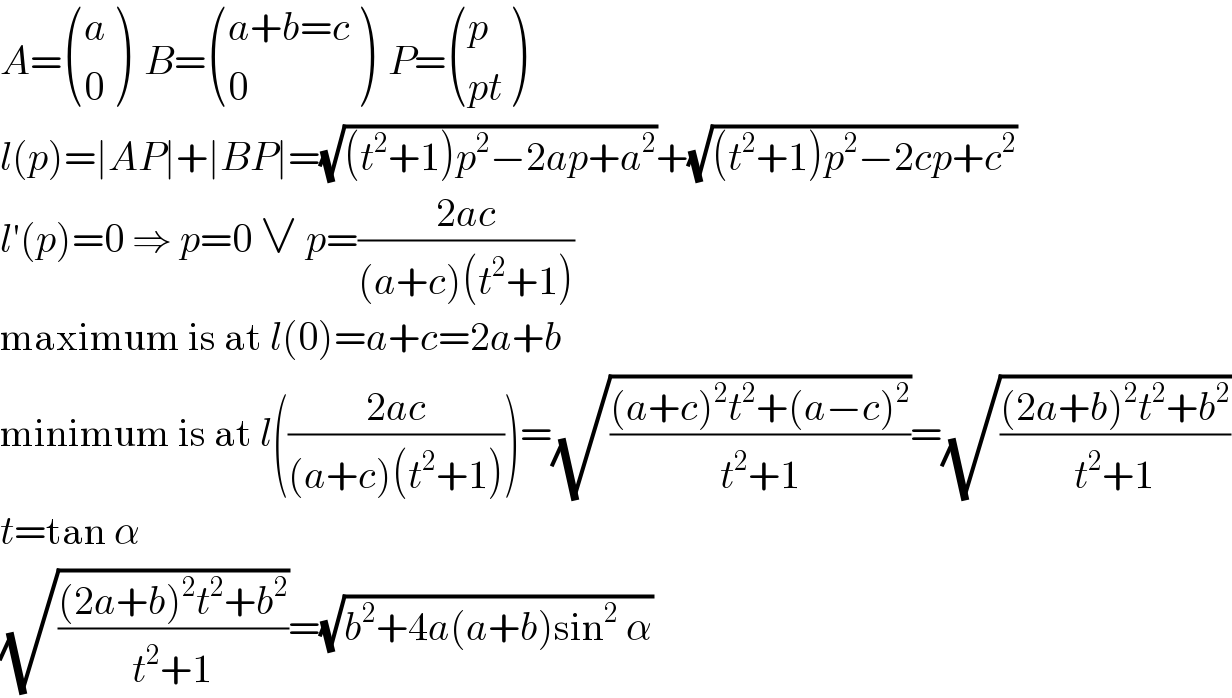
A= ((a),(0) ) B= (((a+b=c)),(0) ) P= ((p),((pt)) ) l(p)=∣AP∣+∣BP∣=(√((t^2 +1)p^2 −2ap+a^2 ))+(√((t^2 +1)p^2 −2cp+c^2 )) l′(p)=0 ⇒ p=0 ∨ p=((2ac)/((a+c)(t^2 +1))) maximum is at l(0)=a+c=2a+b minimum is at l(((2ac)/((a+c)(t^2 +1))))=(√(((a+c)^2 t^2 +(a−c)^2 )/(t^2 +1)))=(√(((2a+b)^2 t^2 +b^2 )/(t^2 +1))) t=tan α (√(((2a+b)^2 t^2 +b^2 )/(t^2 +1)))=(√(b^2 +4a(a+b)sin^2 α))
$${A}=\begin{pmatrix}{{a}}\\{\mathrm{0}}\end{pmatrix}\:\:{B}=\begin{pmatrix}{{a}+{b}={c}}\\{\mathrm{0}}\end{pmatrix}\:\:{P}=\begin{pmatrix}{{p}}\\{{pt}}\end{pmatrix} \\ $$$${l}\left({p}\right)=\mid{AP}\mid+\mid{BP}\mid=\sqrt{\left({t}^{\mathrm{2}} +\mathrm{1}\right){p}^{\mathrm{2}} −\mathrm{2}{ap}+{a}^{\mathrm{2}} }+\sqrt{\left({t}^{\mathrm{2}} +\mathrm{1}\right){p}^{\mathrm{2}} −\mathrm{2}{cp}+{c}^{\mathrm{2}} } \\ $$$${l}'\left({p}\right)=\mathrm{0}\:\Rightarrow\:{p}=\mathrm{0}\:\vee\:{p}=\frac{\mathrm{2}{ac}}{\left({a}+{c}\right)\left({t}^{\mathrm{2}} +\mathrm{1}\right)} \\ $$$$\mathrm{maximum}\:\mathrm{is}\:\mathrm{at}\:{l}\left(\mathrm{0}\right)={a}+{c}=\mathrm{2}{a}+{b} \\ $$$$\mathrm{minimum}\:\mathrm{is}\:\mathrm{at}\:{l}\left(\frac{\mathrm{2}{ac}}{\left({a}+{c}\right)\left({t}^{\mathrm{2}} +\mathrm{1}\right)}\right)=\sqrt{\frac{\left({a}+{c}\right)^{\mathrm{2}} {t}^{\mathrm{2}} +\left({a}−{c}\right)^{\mathrm{2}} }{{t}^{\mathrm{2}} +\mathrm{1}}}=\sqrt{\frac{\left(\mathrm{2}{a}+{b}\right)^{\mathrm{2}} {t}^{\mathrm{2}} +{b}^{\mathrm{2}} }{{t}^{\mathrm{2}} +\mathrm{1}}} \\ $$$${t}=\mathrm{tan}\:\alpha \\ $$$$\sqrt{\frac{\left(\mathrm{2}{a}+{b}\right)^{\mathrm{2}} {t}^{\mathrm{2}} +{b}^{\mathrm{2}} }{{t}^{\mathrm{2}} +\mathrm{1}}}=\sqrt{{b}^{\mathrm{2}} +\mathrm{4}{a}\left({a}+{b}\right)\mathrm{sin}^{\mathrm{2}} \:\alpha} \\ $$
Commented by MJS last updated on 15/Jan/19
not sure what happened before. this is correct and should be the same as your result
$$\mathrm{not}\:\mathrm{sure}\:\mathrm{what}\:\mathrm{happened}\:\mathrm{before}.\:\mathrm{this}\:\mathrm{is}\:\mathrm{correct} \\ $$$$\mathrm{and}\:\mathrm{should}\:\mathrm{be}\:\mathrm{the}\:\mathrm{same}\:\mathrm{as}\:\mathrm{your}\:\mathrm{result} \\ $$
Commented by ajfour last updated on 15/Jan/19
Thanks for the alternative way Sir.
$${Thanks}\:{for}\:{the}\:{alternative}\:{way}\:{Sir}. \\ $$
Commented by mr W last updated on 15/Jan/19
it′s perfect sir! this is a real mathematical solution while my solution is a “physical” one based on “knowledge” that the straight is the shortest path between two points.
$${it}'{s}\:{perfect}\:{sir}! \\ $$$${this}\:{is}\:{a}\:{real}\:{mathematical}\:{solution} \\ $$$${while}\:{my}\:{solution}\:{is}\:{a}\:“{physical}''\:{one} \\ $$$${based}\:{on}\:“{knowledge}''\:{that}\:{the}\:{straight} \\ $$$${is}\:{the}\:{shortest}\:{path}\:{between}\:{two}\:{points}. \\ $$
Commented by mr W last updated on 15/Jan/19
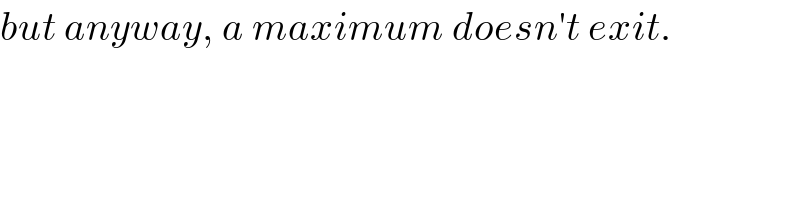
but anyway, a maximum doesn′t exit.
$${but}\:{anyway},\:{a}\:{maximum}\:{doesn}'{t}\:{exit}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *