Question Number 52198 by ajfour last updated on 04/Jan/19

Answered by MJS last updated on 04/Jan/19
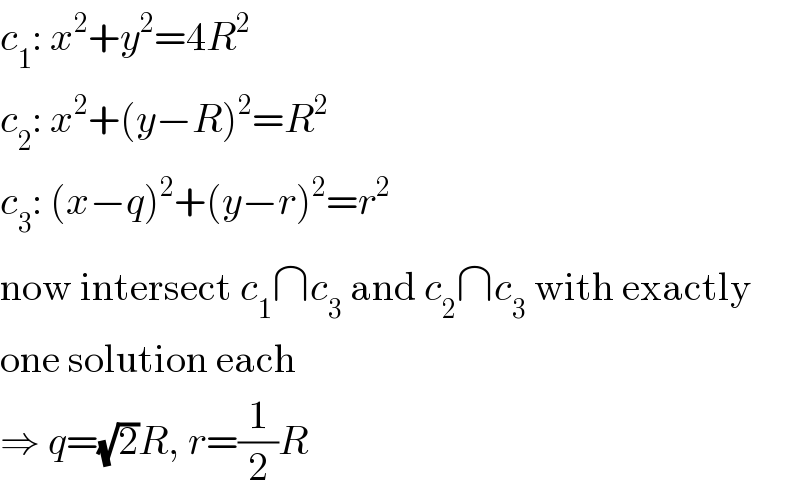
$${c}_{\mathrm{1}} :\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{4}{R}^{\mathrm{2}} \\ $$$${c}_{\mathrm{2}} :\:{x}^{\mathrm{2}} +\left({y}−{R}\right)^{\mathrm{2}} ={R}^{\mathrm{2}} \\ $$$${c}_{\mathrm{3}} :\:\left({x}−{q}\right)^{\mathrm{2}} +\left({y}−{r}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\mathrm{now}\:\mathrm{intersect}\:{c}_{\mathrm{1}} \cap{c}_{\mathrm{3}} \:\mathrm{and}\:{c}_{\mathrm{2}} \cap{c}_{\mathrm{3}} \:\mathrm{with}\:\mathrm{exactly} \\ $$$$\mathrm{one}\:\mathrm{solution}\:\mathrm{each} \\ $$$$\Rightarrow\:{q}=\sqrt{\mathrm{2}}{R},\:{r}=\frac{\mathrm{1}}{\mathrm{2}}{R} \\ $$
Commented by ajfour last updated on 04/Jan/19
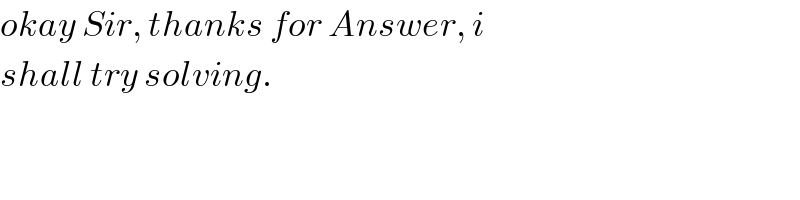
$${okay}\:{Sir},\:{thanks}\:{for}\:{Answer},\:{i} \\ $$$${shall}\:{try}\:{solving}. \\ $$
Answered by mr W last updated on 04/Jan/19
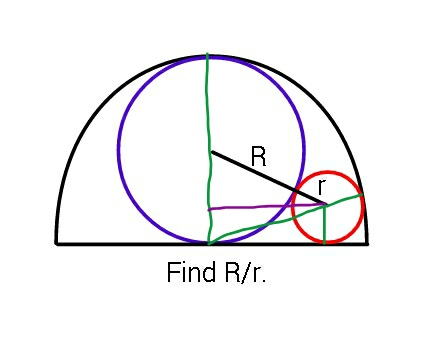
Commented by ajfour last updated on 04/Jan/19

$${Wonderful}\:{Sir}! \\ $$
Commented by mr W last updated on 04/Jan/19
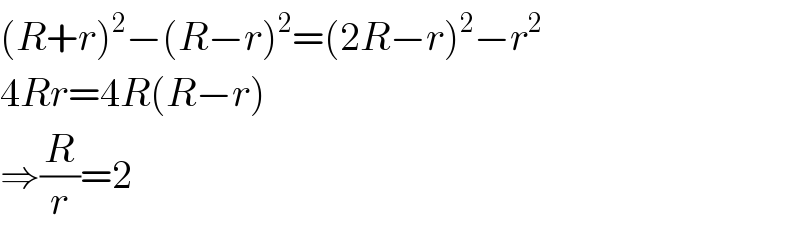
$$\left({R}+{r}\right)^{\mathrm{2}} −\left({R}−{r}\right)^{\mathrm{2}} =\left(\mathrm{2}{R}−{r}\right)^{\mathrm{2}} −{r}^{\mathrm{2}} \\ $$$$\mathrm{4}{Rr}=\mathrm{4}{R}\left({R}−{r}\right) \\ $$$$\Rightarrow\frac{{R}}{{r}}=\mathrm{2} \\ $$
