Question Number 52312 by ajfour last updated on 06/Jan/19
Commented by ajfour last updated on 06/Jan/19
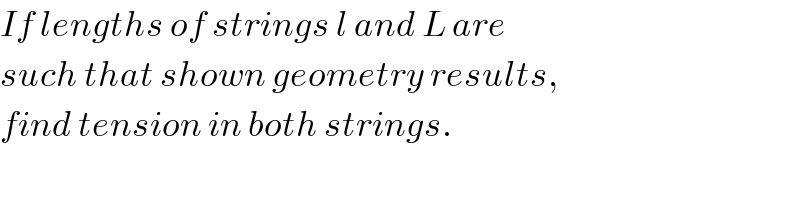
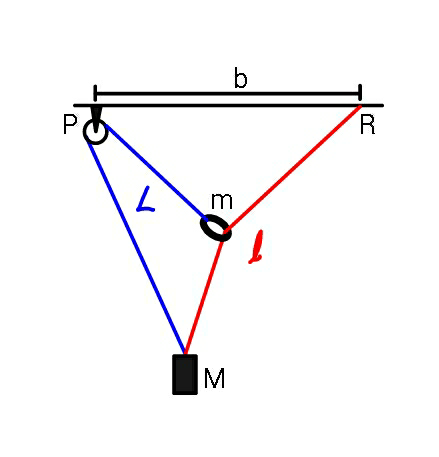
$${If}\:{lengths}\:{of}\:{strings}\:{l}\:{and}\:{L}\:{are} \\ $$$${such}\:{that}\:{shown}\:{geometry}\:{results}, \\ $$$${find}\:{tension}\:{in}\:{both}\:{strings}. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 06/Jan/19
Commented by tanmay.chaudhury50@gmail.com last updated on 06/Jan/19
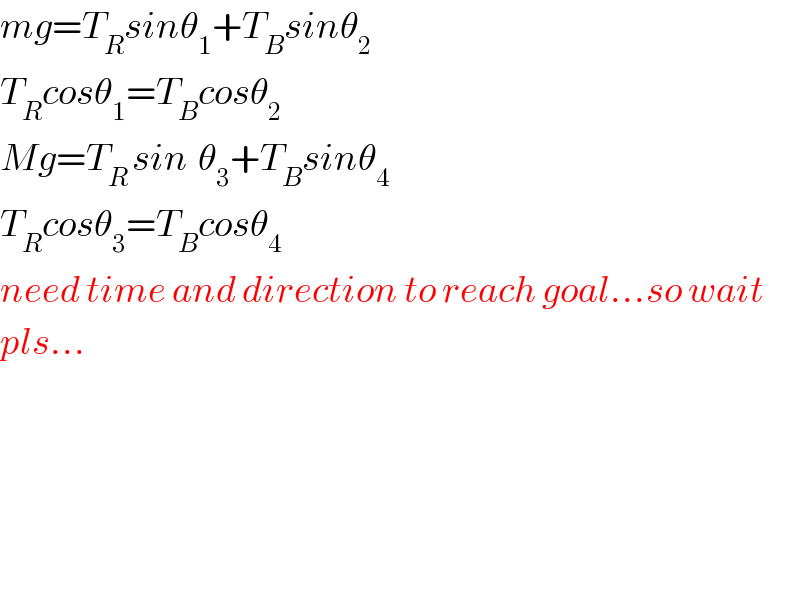
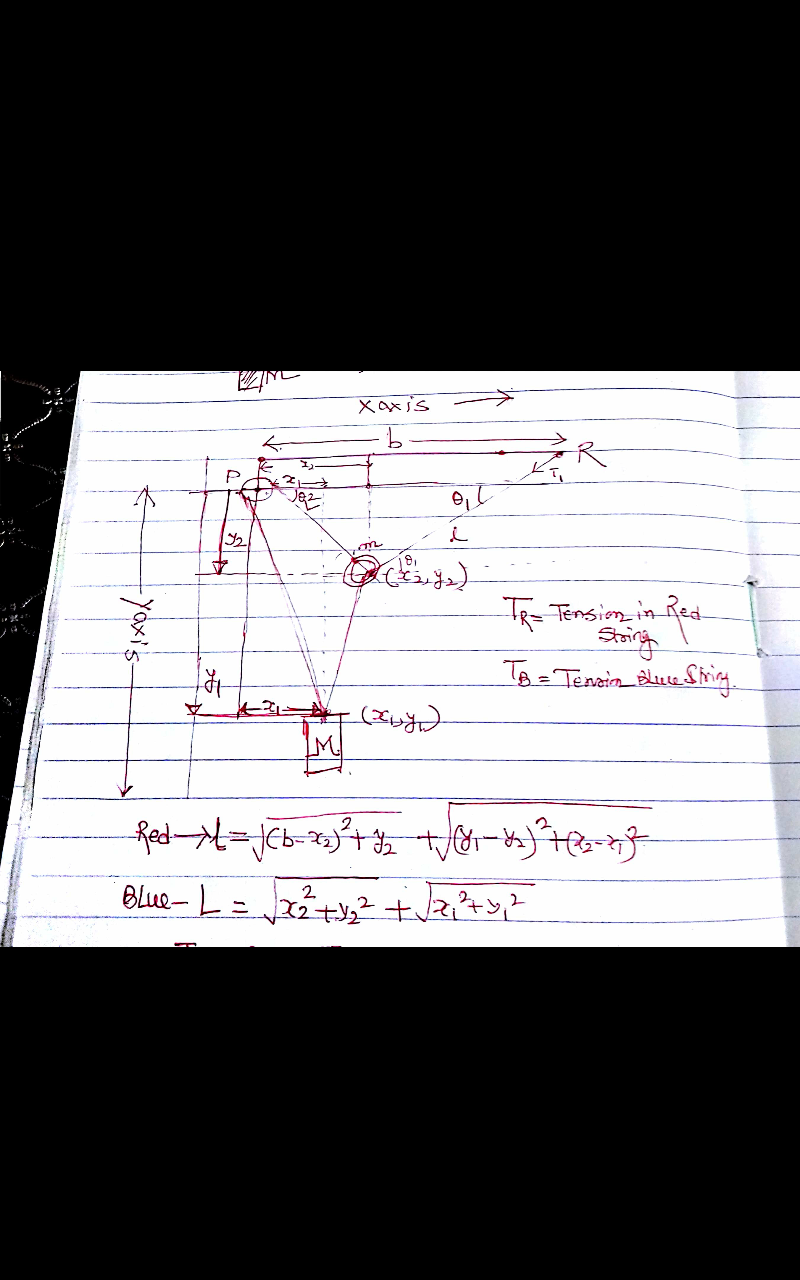
$${mg}={T}_{{R}} {sin}\theta_{\mathrm{1}} +{T}_{{B}} {sin}\theta_{\mathrm{2}} \\ $$$${T}_{{R}} {cos}\theta_{\mathrm{1}} ={T}_{{B}} {cos}\theta_{\mathrm{2}} \\ $$$${Mg}={T}_{{R}\:} {sin}_{} \theta_{\mathrm{3}} +{T}_{{B}} {sin}\theta_{\mathrm{4}} \\ $$$${T}_{{R}} {cos}\theta_{\mathrm{3}} ={T}_{{B}} {cos}\theta_{\mathrm{4}} \\ $$$${need}\:{time}\:{and}\:{direction}\:{to}\:{reach}\:{goal}…{so}\:{wait} \\ $$$${pls}… \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Answered by mr W last updated on 06/Jan/19

Commented by mr W last updated on 06/Jan/19
![let μ=(m/M), λ=(L/b), κ=(l/b) T_1 sin α−T_2 sin δ=0 T_1 cos α+T_2 cos δ=Mg ⇒T_1 =((Mg sin δ)/(sin (α+δ))) ⇒T_2 =((Mg sin α)/(sin (α+δ))) T_1 sin β+T_2 (sin δ−sin γ)=0 T_1 cos β+T_2 (cos γ−cos δ)=mg ⇒T_1 =((mg (sin γ−sin δ))/(sin (β+γ)−sin (β+δ))) ⇒T_2 =((mg sin β)/(sin (β+γ)−sin (β+δ))) ⇒((Mg sin δ)/(sin (α+δ)))=((mg (sin γ−sin δ))/(sin (β+γ)−sin (β+δ))) ⇒((sin δ)/(sin (α+δ)))=((μ (sin γ−sin δ))/(sin (β+γ)−sin (β+δ))) ...(i) ⇒((Mg sin α)/(sin (α+δ)))=((mg sin β)/(sin (β+γ)−sin (β+δ))) ⇒((sin α)/(sin (α+δ)))=((μ sin β)/(sin (β+γ)−sin (β+δ))) ...(ii) ((OR)/(cos β))=((OP)/(cos γ))=(b/(sin (β+γ))) ⇒OR=((cos β b)/(sin (β+γ))) ⇒OP=((cos γ b)/(sin (β+γ))) ∠OPQ=(π/2)−α−((π/2)−β)=β−α ((OQ)/(sin (β−α)))=((OP)/(sin (α+δ)))=((PQ)/(sin (δ+β))) ⇒OQ=((sin (β−α)×OP)/(sin (α+δ)))=((sin (β−α) cos γ b)/(sin (α+δ) sin (β+γ))) ⇒PQ=((sin (δ+β)×OP)/(sin (α+δ)))=((sin (δ+β) cos γ b)/(sin (α+δ) sin (β+γ))) OP+PQ=L ((cos γ b)/(sin (β+γ)))+((sin (δ+β) cos γ b)/(sin (α+δ) sin (β+γ)))=L ⇒((cos γ)/(sin (β+γ)))[1+((sin (δ+β))/(sin (α+δ)))]=λ ...(iii) OR+OQ=l ((cos β b)/(sin (β+γ)))+((sin (β−α) cos γ b)/(sin (α+δ) sin (β+γ)))=l ⇒(1/(sin (β+γ)))[cos β+((sin (β−α) cos γ)/(sin (α+δ)))]=κ ...(iv) 4 eqn. for 4 unknowns: α,β,γ,δ ......](https://www.tinkutara.com/question/Q52350.png)
$${let}\:\mu=\frac{{m}}{{M}},\:\lambda=\frac{{L}}{{b}},\:\kappa=\frac{{l}}{{b}} \\ $$$$ \\ $$$${T}_{\mathrm{1}} \mathrm{sin}\:\alpha−{T}_{\mathrm{2}} \mathrm{sin}\:\delta=\mathrm{0} \\ $$$${T}_{\mathrm{1}} \mathrm{cos}\:\alpha+{T}_{\mathrm{2}} \mathrm{cos}\:\delta={Mg} \\ $$$$\Rightarrow{T}_{\mathrm{1}} =\frac{{Mg}\:\mathrm{sin}\:\delta}{\mathrm{sin}\:\left(\alpha+\delta\right)} \\ $$$$\Rightarrow{T}_{\mathrm{2}} =\frac{{Mg}\:\mathrm{sin}\:\alpha}{\mathrm{sin}\:\left(\alpha+\delta\right)} \\ $$$$ \\ $$$${T}_{\mathrm{1}} \mathrm{sin}\:\beta+{T}_{\mathrm{2}} \left(\mathrm{sin}\:\delta−\mathrm{sin}\:\gamma\right)=\mathrm{0} \\ $$$${T}_{\mathrm{1}} \mathrm{cos}\:\beta+{T}_{\mathrm{2}} \left(\mathrm{cos}\:\gamma−\mathrm{cos}\:\delta\right)={mg} \\ $$$$\Rightarrow{T}_{\mathrm{1}} =\frac{{mg}\:\left(\mathrm{sin}\:\gamma−\mathrm{sin}\:\delta\right)}{\mathrm{sin}\:\left(\beta+\gamma\right)−\mathrm{sin}\:\left(\beta+\delta\right)} \\ $$$$\Rightarrow{T}_{\mathrm{2}} =\frac{{mg}\:\mathrm{sin}\:\beta}{\mathrm{sin}\:\left(\beta+\gamma\right)−\mathrm{sin}\:\left(\beta+\delta\right)} \\ $$$$ \\ $$$$\Rightarrow\frac{{Mg}\:\mathrm{sin}\:\delta}{\mathrm{sin}\:\left(\alpha+\delta\right)}=\frac{{mg}\:\left(\mathrm{sin}\:\gamma−\mathrm{sin}\:\delta\right)}{\mathrm{sin}\:\left(\beta+\gamma\right)−\mathrm{sin}\:\left(\beta+\delta\right)} \\ $$$$\Rightarrow\frac{\mathrm{sin}\:\delta}{\mathrm{sin}\:\left(\alpha+\delta\right)}=\frac{\mu\:\left(\mathrm{sin}\:\gamma−\mathrm{sin}\:\delta\right)}{\mathrm{sin}\:\left(\beta+\gamma\right)−\mathrm{sin}\:\left(\beta+\delta\right)}\:\:\:…\left({i}\right) \\ $$$$\Rightarrow\frac{{Mg}\:\mathrm{sin}\:\alpha}{\mathrm{sin}\:\left(\alpha+\delta\right)}=\frac{{mg}\:\mathrm{sin}\:\beta}{\mathrm{sin}\:\left(\beta+\gamma\right)−\mathrm{sin}\:\left(\beta+\delta\right)} \\ $$$$\Rightarrow\frac{\mathrm{sin}\:\alpha}{\mathrm{sin}\:\left(\alpha+\delta\right)}=\frac{\mu\:\mathrm{sin}\:\beta}{\mathrm{sin}\:\left(\beta+\gamma\right)−\mathrm{sin}\:\left(\beta+\delta\right)}\:\:\:…\left({ii}\right) \\ $$$$ \\ $$$$\frac{{OR}}{\mathrm{cos}\:\beta}=\frac{{OP}}{\mathrm{cos}\:\gamma}=\frac{{b}}{\mathrm{sin}\:\left(\beta+\gamma\right)} \\ $$$$\Rightarrow{OR}=\frac{\mathrm{cos}\:\beta\:{b}}{\mathrm{sin}\:\left(\beta+\gamma\right)} \\ $$$$\Rightarrow{OP}=\frac{\mathrm{cos}\:\gamma\:{b}}{\mathrm{sin}\:\left(\beta+\gamma\right)} \\ $$$$ \\ $$$$\angle{OPQ}=\frac{\pi}{\mathrm{2}}−\alpha−\left(\frac{\pi}{\mathrm{2}}−\beta\right)=\beta−\alpha \\ $$$$\frac{{OQ}}{\mathrm{sin}\:\left(\beta−\alpha\right)}=\frac{{OP}}{\mathrm{sin}\:\left(\alpha+\delta\right)}=\frac{{PQ}}{\mathrm{sin}\:\left(\delta+\beta\right)} \\ $$$$\Rightarrow{OQ}=\frac{\mathrm{sin}\:\left(\beta−\alpha\right)×{OP}}{\mathrm{sin}\:\left(\alpha+\delta\right)}=\frac{\mathrm{sin}\:\left(\beta−\alpha\right)\:\mathrm{cos}\:\gamma\:{b}}{\mathrm{sin}\:\left(\alpha+\delta\right)\:\mathrm{sin}\:\left(\beta+\gamma\right)} \\ $$$$\Rightarrow{PQ}=\frac{\mathrm{sin}\:\left(\delta+\beta\right)×{OP}}{\mathrm{sin}\:\left(\alpha+\delta\right)}=\frac{\mathrm{sin}\:\left(\delta+\beta\right)\:\mathrm{cos}\:\gamma\:{b}}{\mathrm{sin}\:\left(\alpha+\delta\right)\:\mathrm{sin}\:\left(\beta+\gamma\right)} \\ $$$$ \\ $$$${OP}+{PQ}={L} \\ $$$$\frac{\mathrm{cos}\:\gamma\:{b}}{\mathrm{sin}\:\left(\beta+\gamma\right)}+\frac{\mathrm{sin}\:\left(\delta+\beta\right)\:\mathrm{cos}\:\gamma\:{b}}{\mathrm{sin}\:\left(\alpha+\delta\right)\:\mathrm{sin}\:\left(\beta+\gamma\right)}={L} \\ $$$$\Rightarrow\frac{\mathrm{cos}\:\gamma}{\mathrm{sin}\:\left(\beta+\gamma\right)}\left[\mathrm{1}+\frac{\mathrm{sin}\:\left(\delta+\beta\right)}{\mathrm{sin}\:\left(\alpha+\delta\right)}\right]=\lambda\:\:\:…\left({iii}\right) \\ $$$${OR}+{OQ}={l} \\ $$$$\frac{\mathrm{cos}\:\beta\:{b}}{\mathrm{sin}\:\left(\beta+\gamma\right)}+\frac{\mathrm{sin}\:\left(\beta−\alpha\right)\:\mathrm{cos}\:\gamma\:{b}}{\mathrm{sin}\:\left(\alpha+\delta\right)\:\mathrm{sin}\:\left(\beta+\gamma\right)}={l} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{sin}\:\left(\beta+\gamma\right)}\left[\mathrm{cos}\:\beta+\frac{\mathrm{sin}\:\left(\beta−\alpha\right)\:\mathrm{cos}\:\gamma}{\mathrm{sin}\:\left(\alpha+\delta\right)}\right]=\kappa\:\:\:…\left({iv}\right) \\ $$$$ \\ $$$$\mathrm{4}\:{eqn}.\:{for}\:\mathrm{4}\:{unknowns}:\:\alpha,\beta,\gamma,\delta \\ $$$$…… \\ $$
Commented by ajfour last updated on 06/Jan/19

$${Thank}\:{you}\:{Sir},\:{i}\:{could}\:{go}\:{no}\:{further} \\ $$$${too},\:{the}\:{angles}\:{are}\:{intricately} \\ $$$${related},\:{dont}\:{even}\:{permit}\:{us}\:{to}\:{reduce} \\ $$$${them}\:{to}\:{two}\:{eqs}.\:{in}\:{two}\:{unknowns}! \\ $$
