Question-52426

Question Number 52426 by ajfour last updated on 07/Jan/19

Commented by ajfour last updated on 07/Jan/19

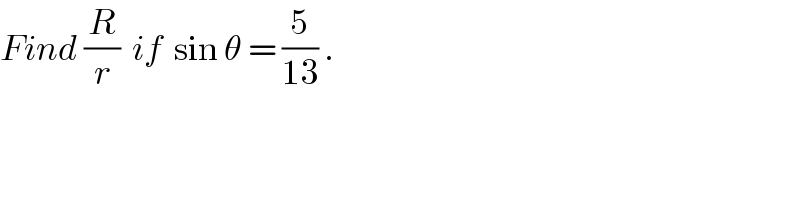
$${Find}\:\frac{{R}}{{r}}\:\:{if}\:\:\mathrm{sin}\:\theta\:=\:\frac{\mathrm{5}}{\mathrm{13}}\:. \\ $$

Answered by mr W last updated on 07/Jan/19

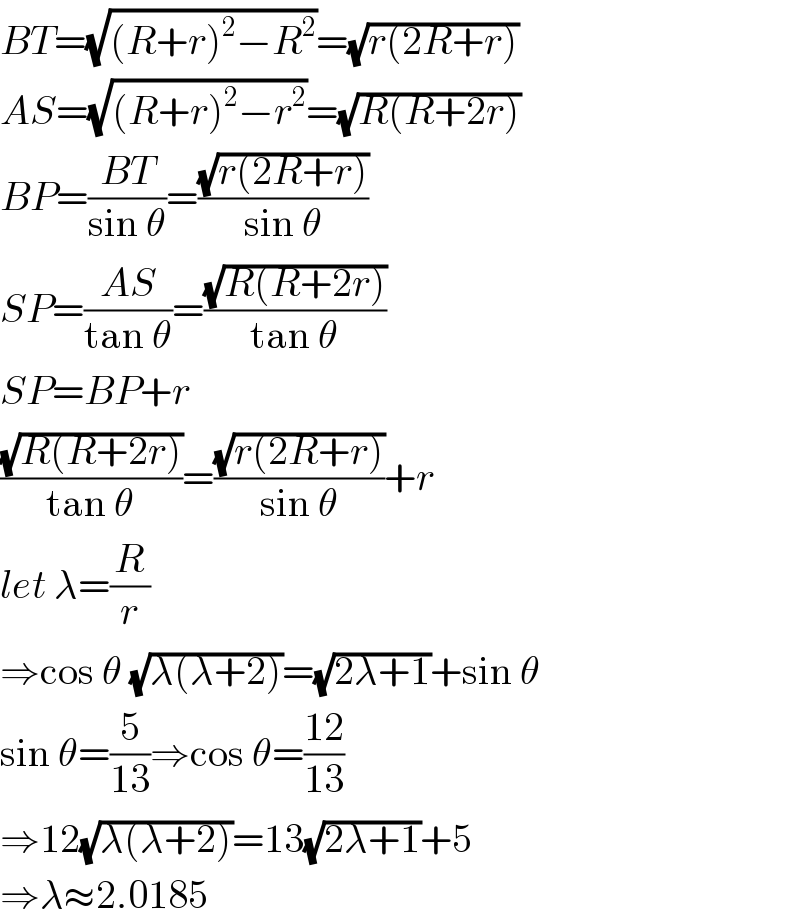
BT=(√((R+r)^2 −R^2 ))=(√(r(2R+r))) AS=(√((R+r)^2 −r^2 ))=(√(R(R+2r))) BP=((BT)/(sin θ))=((√(r(2R+r)))/(sin θ)) SP=((AS)/(tan θ))=((√(R(R+2r)))/(tan θ)) SP=BP+r ((√(R(R+2r)))/(tan θ))=((√(r(2R+r)))/(sin θ))+r let λ=(R/r) ⇒cos θ (√(λ(λ+2)))=(√(2λ+1))+sin θ sin θ=(5/(13))⇒cos θ=((12)/(13)) ⇒12(√(λ(λ+2)))=13(√(2λ+1))+5 ⇒λ≈2.0185

$${BT}=\sqrt{\left({R}+{r}\right)^{\mathrm{2}} −{R}^{\mathrm{2}} }=\sqrt{{r}\left(\mathrm{2}{R}+{r}\right)} \\ $$$${AS}=\sqrt{\left({R}+{r}\right)^{\mathrm{2}} −{r}^{\mathrm{2}} }=\sqrt{{R}\left({R}+\mathrm{2}{r}\right)} \\ $$$${BP}=\frac{{BT}}{\mathrm{sin}\:\theta}=\frac{\sqrt{{r}\left(\mathrm{2}{R}+{r}\right)}}{\mathrm{sin}\:\theta} \\ $$$${SP}=\frac{{AS}}{\mathrm{tan}\:\theta}=\frac{\sqrt{{R}\left({R}+\mathrm{2}{r}\right)}}{\mathrm{tan}\:\theta} \\ $$$${SP}={BP}+{r} \\ $$$$\frac{\sqrt{{R}\left({R}+\mathrm{2}{r}\right)}}{\mathrm{tan}\:\theta}=\frac{\sqrt{{r}\left(\mathrm{2}{R}+{r}\right)}}{\mathrm{sin}\:\theta}+{r} \\ $$$${let}\:\lambda=\frac{{R}}{{r}} \\ $$$$\Rightarrow\mathrm{cos}\:\theta\:\sqrt{\lambda\left(\lambda+\mathrm{2}\right)}=\sqrt{\mathrm{2}\lambda+\mathrm{1}}+\mathrm{sin}\:\theta \\ $$$$\mathrm{sin}\:\theta=\frac{\mathrm{5}}{\mathrm{13}}\Rightarrow\mathrm{cos}\:\theta=\frac{\mathrm{12}}{\mathrm{13}} \\ $$$$\Rightarrow\mathrm{12}\sqrt{\lambda\left(\lambda+\mathrm{2}\right)}=\mathrm{13}\sqrt{\mathrm{2}\lambda+\mathrm{1}}+\mathrm{5} \\ $$$$\Rightarrow\lambda\approx\mathrm{2}.\mathrm{0185} \\ $$

Commented by MJS last updated on 07/Jan/19

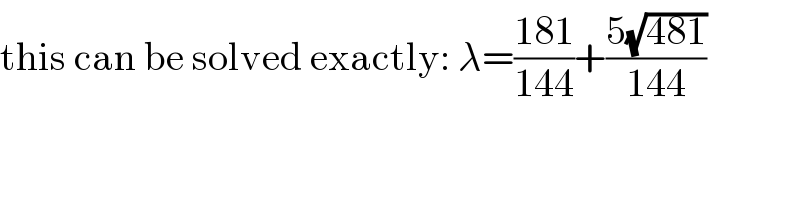
this can be solved exactly: λ=((181)/(144))+((5(√(481)))/(144))

$$\mathrm{this}\:\mathrm{can}\:\mathrm{be}\:\mathrm{solved}\:\mathrm{exactly}:\:\lambda=\frac{\mathrm{181}}{\mathrm{144}}+\frac{\mathrm{5}\sqrt{\mathrm{481}}}{\mathrm{144}} \\ $$

Commented by mr W last updated on 07/Jan/19

$${that}'{s}\:{great}\:{sir}!\:{thanks}! \\ $$

Commented by ajfour last updated on 08/Jan/19

Thank you mrW Sir, Straight and Nice! MjS Sir is very Wise.(Thanks).

$${Thank}\:{you}\:{mrW}\:{Sir},\:\mathcal{S}{traight}\:{and}\:\mathcal{N}{ice}! \\ $$$${MjS}\:{Sir}\:{is}\:{very}\:\mathcal{W}{ise}.\left({Thanks}\right). \\ $$

Answered by mr W last updated on 07/Jan/19

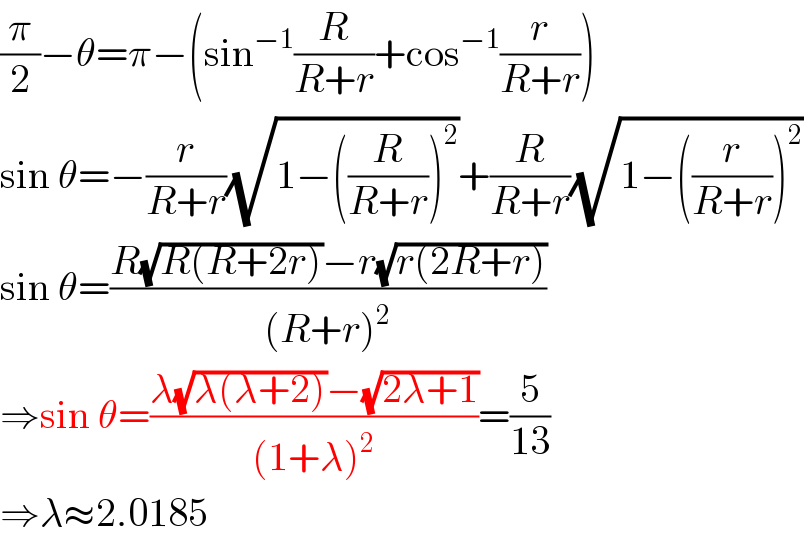
(π/2)−θ=π−(sin^(−1) (R/(R+r))+cos^(−1) (r/(R+r))) sin θ=−(r/(R+r))(√(1−((R/(R+r)))^2 ))+(R/(R+r))(√(1−((r/(R+r)))^2 )) sin θ=((R(√(R(R+2r)))−r(√(r(2R+r))))/((R+r)^2 )) ⇒sin θ=((λ(√(λ(λ+2)))−(√(2λ+1)))/((1+λ)^2 ))=(5/(13)) ⇒λ≈2.0185

$$\frac{\pi}{\mathrm{2}}−\theta=\pi−\left(\mathrm{sin}^{−\mathrm{1}} \frac{{R}}{{R}+{r}}+\mathrm{cos}^{−\mathrm{1}} \frac{{r}}{{R}+{r}}\right) \\ $$$$\mathrm{sin}\:\theta=−\frac{{r}}{{R}+{r}}\sqrt{\mathrm{1}−\left(\frac{{R}}{{R}+{r}}\right)^{\mathrm{2}} }+\frac{{R}}{{R}+{r}}\sqrt{\mathrm{1}−\left(\frac{{r}}{{R}+{r}}\right)^{\mathrm{2}} } \\ $$$$\mathrm{sin}\:\theta=\frac{{R}\sqrt{{R}\left({R}+\mathrm{2}{r}\right)}−{r}\sqrt{{r}\left(\mathrm{2}{R}+{r}\right)}}{\left({R}+{r}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow\mathrm{sin}\:\theta=\frac{\lambda\sqrt{\lambda\left(\lambda+\mathrm{2}\right)}−\sqrt{\mathrm{2}\lambda+\mathrm{1}}}{\left(\mathrm{1}+\lambda\right)^{\mathrm{2}} }=\frac{\mathrm{5}}{\mathrm{13}} \\ $$$$\Rightarrow\lambda\approx\mathrm{2}.\mathrm{0185} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply