Question Number 52468 by mr W last updated on 08/Jan/19
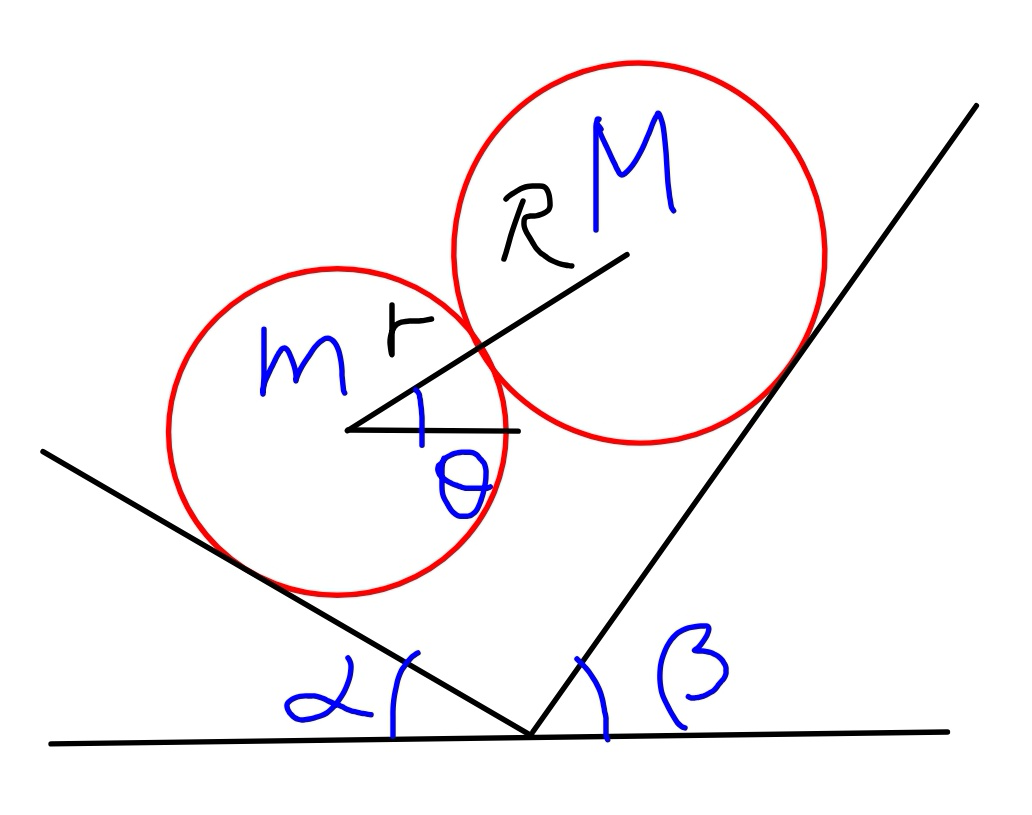
Commented by mr W last updated on 08/Jan/19

$${No}\:{friction}. \\ $$$${Find}\:\theta=? \\ $$
Commented by ajfour last updated on 08/Jan/19
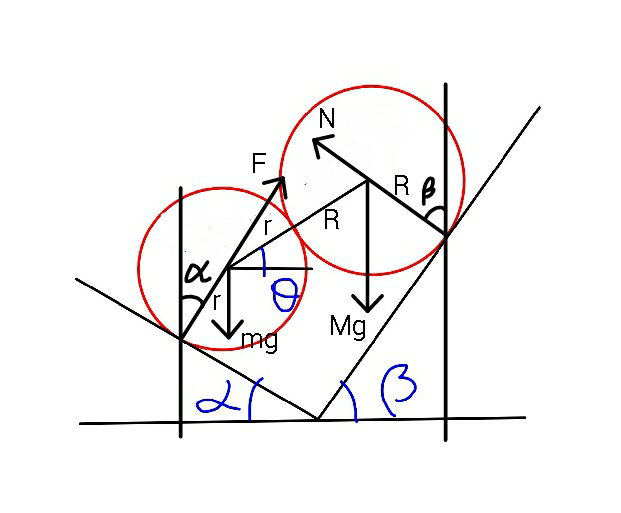
Commented by ajfour last updated on 08/Jan/19
![let mutual reaction force (not shown in figure) be T. Fcos α− Tsin θ= mg ..(i) Ncos β+Tsin θ = Mg ...(ii) Fsin α=Tcos θ = Nsin β ...(iii) hence from (i)÷(ii) & using (iii) ((((cos θcos α)/(sin α))−sin θ)/(((cos θcos β)/(sin β))+sin θ)) = λ (=(m/M)) ⇒ (1/(tan α))−(λ/(tan β)) = (λ+1)tan θ ⇒ θ = tan^(−1) [((tan β−λtan α)/((λ+1)tan αtan β))].](https://www.tinkutara.com/question/Q52475.png)
$${let}\:{mutual}\:{reaction}\:{force}\:\left({not}\:{shown}\right. \\ $$$$\left.{in}\:{figure}\right)\:{be}\:{T}. \\ $$$${F}\mathrm{cos}\:\alpha−\:{T}\mathrm{sin}\:\theta=\:{mg}\:\:\:\:..\left({i}\right) \\ $$$${N}\mathrm{cos}\:\beta+{T}\mathrm{sin}\:\theta\:=\:{Mg}\:\:\:…\left({ii}\right) \\ $$$${F}\mathrm{sin}\:\alpha={T}\mathrm{cos}\:\theta\:=\:{N}\mathrm{sin}\:\beta\:\:\:…\left({iii}\right) \\ $$$${hence}\:{from}\:\left({i}\right)\boldsymbol{\div}\left({ii}\right)\:\&\:{using}\:\left({iii}\right) \\ $$$$\frac{\frac{\mathrm{cos}\:\theta\mathrm{cos}\:\alpha}{\mathrm{sin}\:\alpha}−\mathrm{sin}\:\theta}{\frac{\mathrm{cos}\:\theta\mathrm{cos}\:\beta}{\mathrm{sin}\:\beta}+\mathrm{sin}\:\theta}\:=\:\lambda\:\:\left(=\frac{{m}}{{M}}\right) \\ $$$$\Rightarrow\:\:\frac{\mathrm{1}}{\mathrm{tan}\:\alpha}−\frac{\lambda}{\mathrm{tan}\:\beta}\:=\:\left(\lambda+\mathrm{1}\right)\mathrm{tan}\:\theta \\ $$$$\Rightarrow\:\:\theta\:=\:\mathrm{tan}^{−\mathrm{1}} \left[\frac{\mathrm{tan}\:\beta−\lambda\mathrm{tan}\:\alpha}{\left(\lambda+\mathrm{1}\right)\mathrm{tan}\:\alpha\mathrm{tan}\:\beta}\right]. \\ $$
Commented by mr W last updated on 08/Jan/19
$${thank}\:{you}\:{sir}!\: \\ $$$${answer}\:{is}\:{correct}. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 08/Jan/19
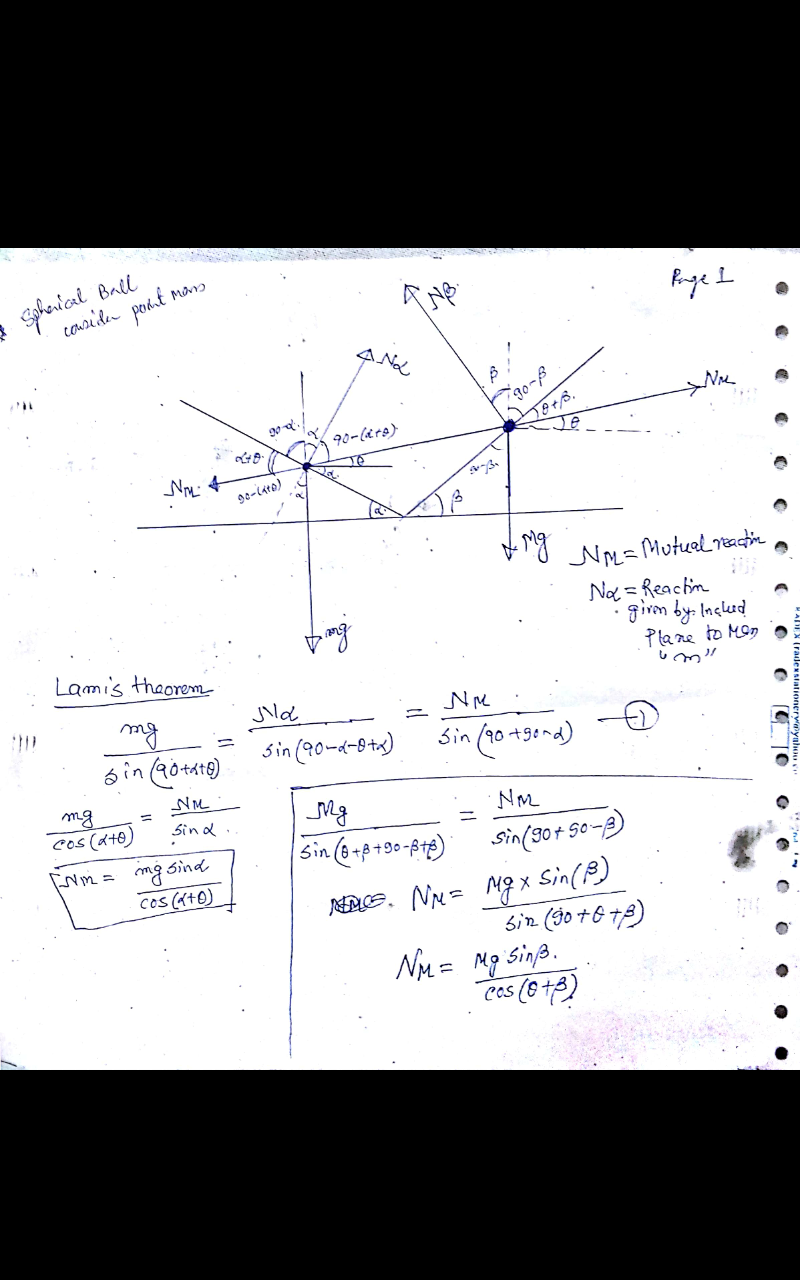
Commented by tanmay.chaudhury50@gmail.com last updated on 08/Jan/19

Commented by mr W last updated on 08/Jan/19

$${thank}\:{you}\:{sir}!\: \\ $$
Answered by mr W last updated on 08/Jan/19
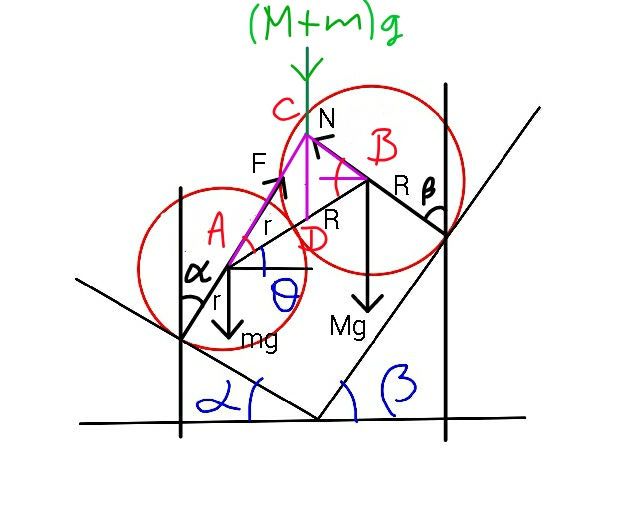
Commented by mr W last updated on 08/Jan/19
![total weight of both balls =(M+m)g its position is in the line CD AD=((M(R+r))/(M+m)) BD=((m(R+r))/(M+m)) in ΔABC: ∠A=(π/2)−α−θ=(π/2)−(α+θ) ∠B=(π/2)−β+θ=(π/2)−(β−θ) CD=((AD×sin ∠A)/(sin α))=((M(R+r))/(M+m))×((cos (α+θ))/(sin α)) CD=((BD×sin ∠B)/(sin β))=((m(R+r))/(M+m))×((cos (β−θ))/(sin β)) ⇒((M(R+r))/(M+m))×((cos (α+θ))/(sin α))=((m(R+r))/(M+m))×((cos (β−θ))/(sin β)) ⇒((cos (α+θ))/(sin α))=(m/M)×((cos (β−θ))/(sin β)) with λ=(m/M) ⇒((cos θ)/(tan α))−sin θ=λ(((cos θ)/(tan β))+sin θ) ⇒tan θ=(1/(1+λ))((1/(tan α))−(λ/(tan β))) ⇒θ=tan^(−1) [(1/(1+λ))((1/(tan α))−(λ/(tan β)))]](https://www.tinkutara.com/question/Q52492.png)
$${total}\:{weight}\:{of}\:{both}\:{balls}\:=\left({M}+{m}\right){g} \\ $$$${its}\:{position}\:{is}\:{in}\:{the}\:{line}\:{CD} \\ $$$${AD}=\frac{{M}\left({R}+{r}\right)}{{M}+{m}} \\ $$$${BD}=\frac{{m}\left({R}+{r}\right)}{{M}+{m}} \\ $$$${in}\:\Delta{ABC}: \\ $$$$\angle{A}=\frac{\pi}{\mathrm{2}}−\alpha−\theta=\frac{\pi}{\mathrm{2}}−\left(\alpha+\theta\right) \\ $$$$\angle{B}=\frac{\pi}{\mathrm{2}}−\beta+\theta=\frac{\pi}{\mathrm{2}}−\left(\beta−\theta\right) \\ $$$${CD}=\frac{{AD}×\mathrm{sin}\:\angle{A}}{\mathrm{sin}\:\alpha}=\frac{{M}\left({R}+{r}\right)}{{M}+{m}}×\frac{\mathrm{cos}\:\left(\alpha+\theta\right)}{\mathrm{sin}\:\alpha} \\ $$$${CD}=\frac{{BD}×\mathrm{sin}\:\angle{B}}{\mathrm{sin}\:\beta}=\frac{{m}\left({R}+{r}\right)}{{M}+{m}}×\frac{\mathrm{cos}\:\left(\beta−\theta\right)}{\mathrm{sin}\:\beta} \\ $$$$\Rightarrow\frac{{M}\left({R}+{r}\right)}{{M}+{m}}×\frac{\mathrm{cos}\:\left(\alpha+\theta\right)}{\mathrm{sin}\:\alpha}=\frac{{m}\left({R}+{r}\right)}{{M}+{m}}×\frac{\mathrm{cos}\:\left(\beta−\theta\right)}{\mathrm{sin}\:\beta} \\ $$$$\Rightarrow\frac{\mathrm{cos}\:\left(\alpha+\theta\right)}{\mathrm{sin}\:\alpha}=\frac{{m}}{{M}}×\frac{\mathrm{cos}\:\left(\beta−\theta\right)}{\mathrm{sin}\:\beta} \\ $$$${with}\:\lambda=\frac{{m}}{{M}} \\ $$$$\Rightarrow\frac{\mathrm{cos}\:\theta}{\mathrm{tan}\:\alpha}−\mathrm{sin}\:\theta=\lambda\left(\frac{\mathrm{cos}\:\theta}{\mathrm{tan}\:\beta}+\mathrm{sin}\:\theta\right) \\ $$$$\Rightarrow\mathrm{tan}\:\theta=\frac{\mathrm{1}}{\mathrm{1}+\lambda}\left(\frac{\mathrm{1}}{\mathrm{tan}\:\alpha}−\frac{\lambda}{\mathrm{tan}\:\beta}\right) \\ $$$$\Rightarrow\theta=\mathrm{tan}^{−\mathrm{1}} \left[\frac{\mathrm{1}}{\mathrm{1}+\lambda}\left(\frac{\mathrm{1}}{\mathrm{tan}\:\alpha}−\frac{\lambda}{\mathrm{tan}\:\beta}\right)\right] \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 09/Jan/19
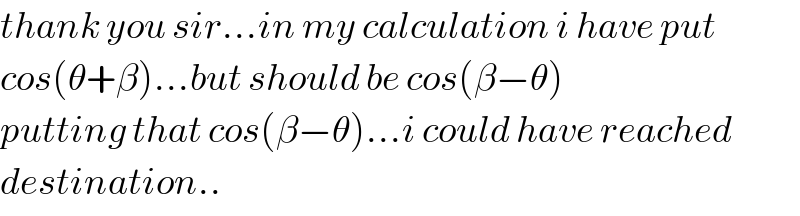
$${thank}\:{you}\:{sir}…{in}\:{my}\:{calculation}\:{i}\:{have}\:{put} \\ $$$${cos}\left(\theta+\beta\right)…{but}\:{should}\:{be}\:{cos}\left(\beta−\theta\right) \\ $$$${putting}\:{that}\:{cos}\left(\beta−\theta\right)…{i}\:{could}\:{have}\:{reached} \\ $$$${destination}.. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 09/Jan/19
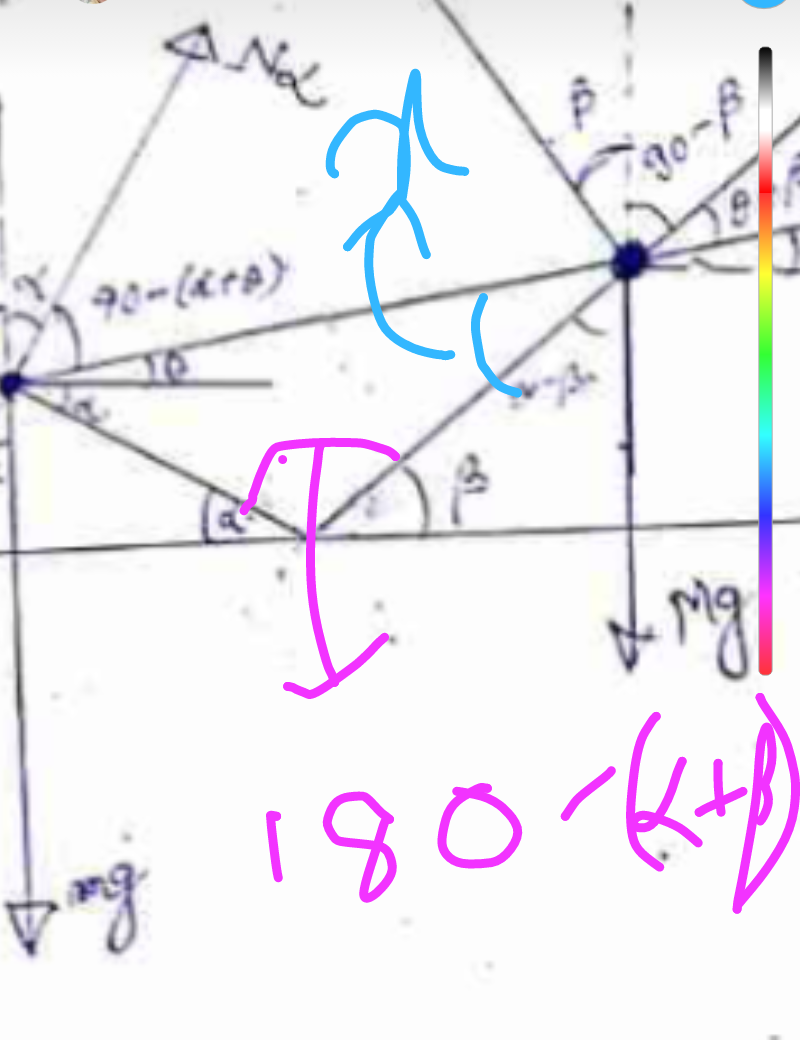
Commented by tanmay.chaudhury50@gmail.com last updated on 09/Jan/19

Commented by mr W last updated on 09/Jan/19
$${thanks}\:{for}\:{your}\:{efforts}\:{sir}! \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 09/Jan/19

$${thank}\:{you}\:{sir}… \\ $$
