Question Number 52487 by ajfour last updated on 08/Jan/19

Commented by ajfour last updated on 08/Jan/19
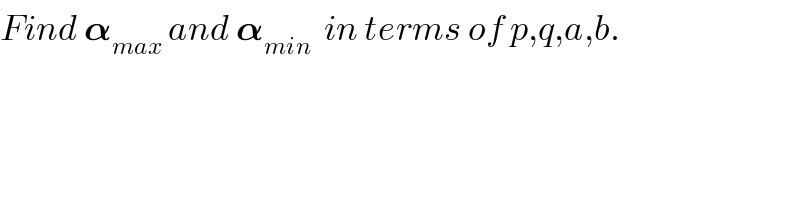
$${Find}\:\boldsymbol{\alpha}_{{max}} \:{and}\:\boldsymbol{\alpha}_{{min}} \:\:{in}\:{terms}\:{of}\:{p},{q},{a},{b}. \\ $$
Commented by mr W last updated on 09/Jan/19
$${question}\:{seems}\:{to}\:{be}\:{very}\:{hard}. \\ $$
Commented by ajfour last updated on 09/Jan/19

$${yes}\:{sir},\:{let}\:{MjS}\:{Sir}\:{enlighten}\:{us}. \\ $$
Commented by MJS last updated on 09/Jan/19

$$…\mathrm{trying}… \\ $$
Commented by MJS last updated on 09/Jan/19
$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{think}\:\mathrm{we}\:\mathrm{can}\:\mathrm{solve}\:\mathrm{this}. \\ $$$$\mathrm{it}'\mathrm{s}\:\mathrm{even}\:\mathrm{hard}\:\mathrm{with}\:\mathrm{given}\:\mathrm{values}\:\mathrm{for}\:{a},\:{b},\:{p},\:{q} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 09/Jan/19

$${i}\:{have}\:{some}\:{comments}\:{regarding}\:{this}\:{question} \\ $$$${pls}\:{reply}\:{who}\:{posted}\:{the}\:{question}… \\ $$$$\left.\mathrm{1}\right){are}\:{length}\:{p}\:{and}\:{q}\:{constant}\:{value}..{to}\:{find} \\ $$$${max}\:\alpha\:{point}\:{P}\:\:{and}\:{Q}\:{have}\:{to}\:\:{move}\:{away}\:{along} \\ $$$${the}\:{elliptical}\:{path}…{then}\:{how}\:{the}\:{length}\:{PR}\:{that} \\ $$$${is}\:{q}\:{and}\:{QR}\:{that}\:{is}\:{p}\:{remain}\:{same}… \\ $$$${value}\:{of}\:{p}\:{and}\:{q}\:{must}\:{change} \\ $$$$\left.\mathrm{2}\right){for}\:{min}\:\propto\:{point}\:{P}\:{and}\:{Q}\:{come}\:{closer} \\ $$$${as}\:{a}\:{results}\:{length}\:{p}\:{snd}\:{q}\:{get}\:{reduced}. \\ $$$${for}\:{max}\:\alpha\:{length}\:{p}\:{and}\:{q}\:{get}\:{increased}. \\ $$$$\left.\mathrm{3}\right){what}\:{is}\:{the}\:{basis}\:{of}\:{this}\:{question}… \\ $$$${for}\:{the}\:{given}\:{figure}\:{cos}\alpha=\frac{{PR}^{\mathrm{2}} +{QR}^{\mathrm{2}} −{PQ}^{\mathrm{2}} }{\mathrm{2}×{PR}×{QR}} \\ $$$${cos}\alpha=\frac{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} −\left({PQ}\right)_{{constant}\:{value}} ^{\mathrm{2}} }{\mathrm{2}{pq}} \\ $$$${then}\:\bigtriangleup\alpha=\mathrm{0} \\ $$$${so}\:{pls}\:{clarify}\:{the}\:{question}\:{clearly}… \\ $$$$ \\ $$
Commented by ajfour last updated on 09/Jan/19
$${okay}\:{MjS}\:{Sir},\:{thanks}\:{for}\:{giving}\:{it}\:{a}\:{try}. \\ $$
Commented by ajfour last updated on 09/Jan/19
$${i}'{m}\:{very}\:{sorry}\:{Tanmay}\:{Sir},\:{question} \\ $$$${might}\:{not}\:{be}\:{correct}\:{for}\:{you}. \\ $$
Commented by MJS last updated on 09/Jan/19
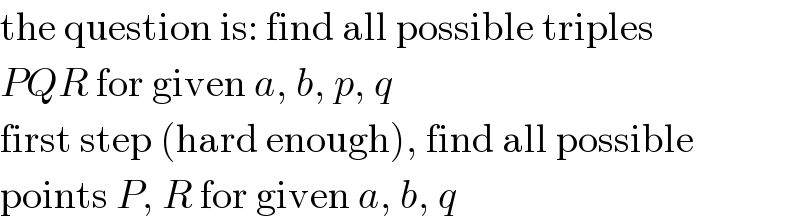
$$\mathrm{the}\:\mathrm{question}\:\mathrm{is}:\:\mathrm{find}\:\mathrm{all}\:\mathrm{possible}\:\mathrm{triples}\: \\ $$$${PQR}\:\mathrm{for}\:\mathrm{given}\:{a},\:{b},\:{p},\:{q} \\ $$$$\mathrm{first}\:\mathrm{step}\:\left(\mathrm{hard}\:\mathrm{enough}\right),\:\mathrm{find}\:\mathrm{all}\:\mathrm{possible} \\ $$$$\mathrm{points}\:{P},\:{R}\:\mathrm{for}\:\mathrm{given}\:{a},\:{b},\:{q} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 09/Jan/19

$${do}\:{the}\:{questin}\:{itself}\:{a}\:{valid}\:{question}…{if}\:{so}\:{there} \\ $$$${must}\:{be}\:{co}\:{relation}\:{among}\:{p},{q}\:{and}\:\alpha \\ $$$${some}\:{statement}\:{is}\:{missing}…{co}\:{relation} \\ $$$${among}\:{p}\:{and}\:{q}\:\:{and}\:\alpha… \\ $$
Commented by ajfour last updated on 09/Jan/19

Commented by ajfour last updated on 09/Jan/19
![let R(acos θ, bsin θ) P[acos θ−pcos (θ+φ), bsin θ−psin (θ+φ)] Q(acos θ−qcos φ, bsin θ−qsin φ) let us call cos θ = c_0 , cos φ= c_1 , cos (θ+φ)=c_2 , sin θ=s_0 , sin φ= s_1 , sin (θ+φ)= s_2 . P is on ellipse, so (((ac_0 −qc_1 )^2 )/a^2 )+(((bs_0 −qs_1 )^2 )/b^2 ) = 1 ⇒ ((qc_1 ^2 )/a^2 )+((qs_1 ^2 )/b^2 ) = (2/(ab))(ac_0 c_1 +bs_0 s_1 ) similarly for Q on ellipse, ⇒ ((pc_2 ^2 )/a^2 )+((ps_2 ^2 )/b^2 ) = (2/(ab))(ac_0 c_2 +bs_0 s_2 ) _________________________ rewriting ac_0 c_1 +bs_0 s_1 = (q/(ab))(b^2 c_1 ^2 +a^2 s_1 ^2 )=(q/(ab))h_1 ac_0 c_2 +bs_0 s_2 = (p/(ab))(b^2 c_2 +a^2 s_2 ^2 )=(p/(ab))h_2 from these two eqs. c_0 = ( determinant ((((qh_1 )/(ab)),(bs_1 )),(((ph_2 )/(ab)),(bs_2 )))_ / determinant (((ac_1 ),(bs_1 )),((ac_2 ),(bs_2 )))^ ) , s_0 = ( determinant (((ac_1 ),((qh_1 )/(ab))),((ac_2 ),((ph_2 )/(ab))))_ / determinant (((ac_1 ),(bs_1 )),((ac_2 ),(bs_2 )))^ ) Now c_0 ^2 +s_0 ^2 = 1 ⇒ b^2 (((qh_1 s_2 −ph_2 s_1 )/(s_2 c_1 −c_2 s_1 )))^2 +a^2 (((ph_2 c_1 −qh_1 c_2 )/(s_2 c_1 −c_2 s_1 )))^2 = a^4 b^4 but s_2 c_1 −c_2 s_1 = sin (φ+α)cos φ−cos (φ+α)sin φ = sin α hence b^2 {qsin (φ+α)[b^2 cos^2 φ+a^2 sin^2 φ] −psin φ[b^2 cos^2 (φ+α)+a^2 sin^2 (φ+α)]}^2 +a^2 {pcos φ[b^2 cos^2 (φ+α)+a^2 sin^2 (φ+α)] −qcos (φ+α)[b^2 cos^2 φ+a^2 sin^2 φ]}^2 = a^4 b^4 sin^2 α And with (dα/dφ) = 0, φ can be obtained; hence 𝛂_(max) and 𝛂_(min) .](https://www.tinkutara.com/question/Q52545.png)
$${let}\:{R}\left({a}\mathrm{cos}\:\theta,\:{b}\mathrm{sin}\:\theta\right) \\ $$$${P}\left[{a}\mathrm{cos}\:\theta−{p}\mathrm{cos}\:\left(\theta+\phi\right),\:{b}\mathrm{sin}\:\theta−{p}\mathrm{sin}\:\left(\theta+\phi\right)\right] \\ $$$${Q}\left({a}\mathrm{cos}\:\theta−{q}\mathrm{cos}\:\phi,\:{b}\mathrm{sin}\:\theta−{q}\mathrm{sin}\:\phi\right) \\ $$$${let}\:{us}\:{call}\:\:\mathrm{cos}\:\theta\:=\:{c}_{\mathrm{0}} \:,\:\mathrm{cos}\:\phi=\:{c}_{\mathrm{1}} , \\ $$$$\mathrm{cos}\:\left(\theta+\phi\right)={c}_{\mathrm{2}} \:,\:\mathrm{sin}\:\theta={s}_{\mathrm{0}} \:,\:\mathrm{sin}\:\phi=\:{s}_{\mathrm{1}} , \\ $$$$\mathrm{sin}\:\left(\theta+\phi\right)=\:{s}_{\mathrm{2}} \:. \\ $$$$\:\:{P}\:\:{is}\:{on}\:{ellipse},\:{so} \\ $$$$\:\:\frac{\left({ac}_{\mathrm{0}} −{qc}_{\mathrm{1}} \right)^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{\left({bs}_{\mathrm{0}} −{qs}_{\mathrm{1}} \right)^{\mathrm{2}} }{{b}^{\mathrm{2}} }\:=\:\mathrm{1} \\ $$$$\Rightarrow\:\frac{{qc}_{\mathrm{1}} ^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{qs}_{\mathrm{1}} ^{\mathrm{2}} }{{b}^{\mathrm{2}} }\:=\:\frac{\mathrm{2}}{{ab}}\left({ac}_{\mathrm{0}} {c}_{\mathrm{1}} +{bs}_{\mathrm{0}} {s}_{\mathrm{1}} \right) \\ $$$${similarly}\:{for}\:{Q}\:{on}\:{ellipse}, \\ $$$$\Rightarrow\:\frac{{pc}_{\mathrm{2}} ^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{ps}_{\mathrm{2}} ^{\mathrm{2}} }{{b}^{\mathrm{2}} }\:=\:\frac{\mathrm{2}}{{ab}}\left({ac}_{\mathrm{0}} {c}_{\mathrm{2}} +{bs}_{\mathrm{0}} {s}_{\mathrm{2}} \right) \\ $$$$\:\:\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$$\:{rewriting} \\ $$$$\:\:{ac}_{\mathrm{0}} {c}_{\mathrm{1}} +{bs}_{\mathrm{0}} {s}_{\mathrm{1}} =\:\frac{{q}}{{ab}}\left({b}^{\mathrm{2}} {c}_{\mathrm{1}} ^{\mathrm{2}} +{a}^{\mathrm{2}} {s}_{\mathrm{1}} ^{\mathrm{2}} \right)=\frac{{q}}{{ab}}{h}_{\mathrm{1}} \\ $$$$\:\:{ac}_{\mathrm{0}} {c}_{\mathrm{2}} +{bs}_{\mathrm{0}} {s}_{\mathrm{2}} \:=\:\frac{{p}}{{ab}}\left({b}^{\mathrm{2}} {c}_{\mathrm{2}} +{a}^{\mathrm{2}} {s}_{\mathrm{2}} ^{\mathrm{2}} \right)=\frac{{p}}{{ab}}{h}_{\mathrm{2}} \\ $$$${from}\:{these}\:{two}\:{eqs}. \\ $$$$\:\:\:{c}_{\mathrm{0}} \:=\:\frac{\begin{vmatrix}{\frac{{qh}_{\mathrm{1}} }{{ab}}}&{{bs}_{\mathrm{1}} }\\{\frac{{ph}_{\mathrm{2}} }{{ab}}}&{{bs}_{\mathrm{2}} }\end{vmatrix}_{} }{\begin{vmatrix}{{ac}_{\mathrm{1}} }&{{bs}_{\mathrm{1}} }\\{{ac}_{\mathrm{2}} }&{{bs}_{\mathrm{2}} }\end{vmatrix}^{} }\:\:,\:{s}_{\mathrm{0}} \:=\:\frac{\begin{vmatrix}{{ac}_{\mathrm{1}} }&{\frac{{qh}_{\mathrm{1}} }{{ab}}}\\{{ac}_{\mathrm{2}} }&{\frac{{ph}_{\mathrm{2}} }{{ab}}}\end{vmatrix}_{} }{\begin{vmatrix}{{ac}_{\mathrm{1}} }&{{bs}_{\mathrm{1}} }\\{{ac}_{\mathrm{2}} }&{{bs}_{\mathrm{2}} }\end{vmatrix}^{} } \\ $$$${Now}\:\:{c}_{\mathrm{0}} ^{\mathrm{2}} +{s}_{\mathrm{0}} ^{\mathrm{2}} \:=\:\mathrm{1} \\ $$$$\Rightarrow\:{b}^{\mathrm{2}} \left(\frac{{qh}_{\mathrm{1}} {s}_{\mathrm{2}} −{ph}_{\mathrm{2}} {s}_{\mathrm{1}} }{{s}_{\mathrm{2}} {c}_{\mathrm{1}} −{c}_{\mathrm{2}} {s}_{\mathrm{1}} }\right)^{\mathrm{2}} +{a}^{\mathrm{2}} \left(\frac{{ph}_{\mathrm{2}} {c}_{\mathrm{1}} −{qh}_{\mathrm{1}} {c}_{\mathrm{2}} }{{s}_{\mathrm{2}} {c}_{\mathrm{1}} −{c}_{\mathrm{2}} {s}_{\mathrm{1}} }\right)^{\mathrm{2}} =\:{a}^{\mathrm{4}} {b}^{\mathrm{4}} \\ $$$${but}\:\:{s}_{\mathrm{2}} {c}_{\mathrm{1}} −{c}_{\mathrm{2}} {s}_{\mathrm{1}} \:=\:\mathrm{sin}\:\left(\phi+\alpha\right)\mathrm{cos}\:\phi−\mathrm{cos}\:\left(\phi+\alpha\right)\mathrm{sin}\:\phi \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{sin}\:\alpha \\ $$$${hence} \\ $$$${b}^{\mathrm{2}} \left\{{q}\mathrm{sin}\:\left(\phi+\alpha\right)\left[{b}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \phi+{a}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \phi\right]\right. \\ $$$$\left.\:\:\:\:\:\:\:−{p}\mathrm{sin}\:\phi\left[{b}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \left(\phi+\alpha\right)+{a}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \left(\phi+\alpha\right)\right]\right\}^{\mathrm{2}} \\ $$$$\:\:+{a}^{\mathrm{2}} \left\{{p}\mathrm{cos}\:\phi\left[{b}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \left(\phi+\alpha\right)+{a}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \left(\phi+\alpha\right)\right]\right. \\ $$$$\left.\:\:\:\:\:\:\:−{q}\mathrm{cos}\:\left(\phi+\alpha\right)\left[{b}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \phi+{a}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \phi\right]\right\}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:{a}^{\mathrm{4}} {b}^{\mathrm{4}} \mathrm{sin}\:^{\mathrm{2}} \alpha \\ $$$${And}\:{with}\:\frac{{d}\alpha}{{d}\phi}\:=\:\mathrm{0},\:\phi\:{can}\:{be}\:{obtained}; \\ $$$${hence}\:\boldsymbol{\alpha}_{{max}} \:{and}\:\boldsymbol{\alpha}_{{min}} . \\ $$
Commented by MJS last updated on 09/Jan/19

$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{think}\:\mathrm{this}\:\mathrm{is}\:\mathrm{necessary} \\ $$$$\mathrm{we}\:\mathrm{can}\:“\mathrm{rotate}''\:{PR}\:\mathrm{around}\:\mathrm{the}\:\mathrm{ellipse}. \\ $$$$\mathrm{for}\:\mathrm{any}\:\mathrm{chosen}\:{R}\:\mathrm{there}\:\mathrm{are}\:\left(\mathrm{depending}\:\mathrm{on}\:{q}\right) \\ $$$$\mathrm{0},\:\mathrm{1},\:\mathrm{2},\:\mathrm{3}\:\mathrm{or}\:\mathrm{4}\:\mathrm{possible}\:\mathrm{positions}\:\mathrm{for}\:{P} \\ $$$$\left(\mathrm{the}\:\mathrm{problem}\:\mathrm{is},\:\mathrm{we}\:\mathrm{cannot}\:\mathrm{generally}\:\mathrm{solve}\:\right. \\ $$$$\left.\mathrm{a}\:\mathrm{polynome}\:\mathrm{of}\:\mathrm{4}^{\mathrm{th}} \:\mathrm{degree}\right) \\ $$$$\mathrm{same}\:\mathrm{for}\:{QR}\:\left({p}\right) \\ $$$$\mathrm{try}\:\mathrm{with} \\ $$$${a}=\mathrm{5}\:{b}=\mathrm{3}\:\left(\mathrm{1}\right)\:{p}=\mathrm{7}\:{q}=\mathrm{9}\:\left(\mathrm{2}\right)\:{p}=\mathrm{4}\:{q}=\mathrm{6} \\ $$$$\mathrm{to}\:\mathrm{see}\:\mathrm{where}\:\mathrm{and}\:\mathrm{how}\:\mathrm{the}\:\mathrm{problems}\:\mathrm{occur} \\ $$$$\mathrm{we}\:\mathrm{need}\:\mathrm{to}\:\mathrm{make}\:\mathrm{out}\:\mathrm{different}\:\mathrm{cases}… \\ $$$$…\mathrm{this}\:\mathrm{was}\:\mathrm{to}\:\mathrm{the}\:\mathrm{former}\:\mathrm{comment}\:\mathrm{of}\:\mathrm{Sir} \\ $$$$\mathrm{Tanmay} \\ $$
