Question Number 52558 by ajfour last updated on 09/Jan/19
Commented by ajfour last updated on 10/Jan/19
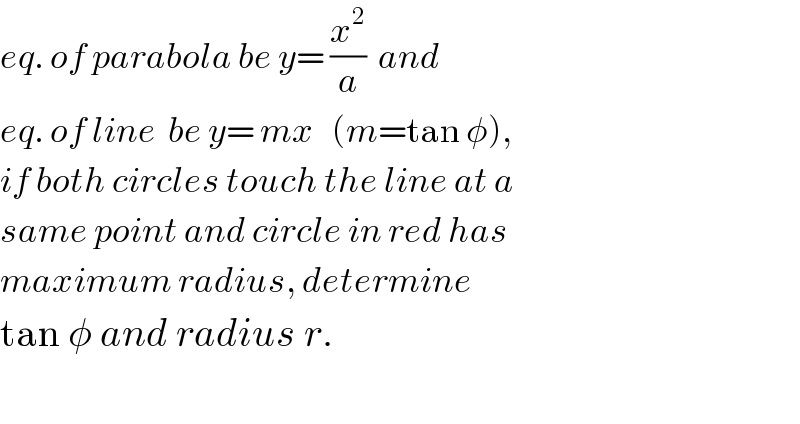
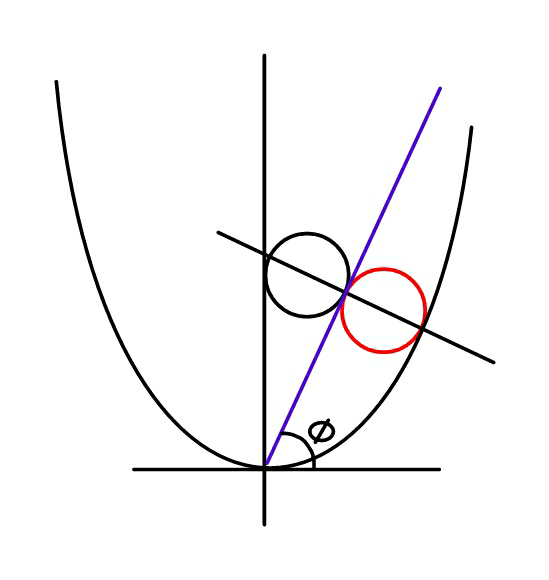
$${eq}.\:{of}\:{parabola}\:{be}\:{y}=\:\frac{{x}^{\mathrm{2}} }{{a}}\:\:{and} \\ $$$${eq}.\:{of}\:{line}\:\:{be}\:{y}=\:{mx}\:\:\:\left({m}=\mathrm{tan}\:\phi\right), \\ $$$${if}\:{both}\:{circles}\:{touch}\:{the}\:{line}\:{at}\:{a} \\ $$$${same}\:{point}\:{and}\:{circle}\:{in}\:{red}\:{has} \\ $$$${maximum}\:{radius},\:{determine} \\ $$$$\mathrm{tan}\:\phi\:{and}\:{radius}\:{r}. \\ $$$$ \\ $$
Commented by ajfour last updated on 10/Jan/19
Commented by ajfour last updated on 10/Jan/19
![y= (x^2 /a) ⇒ tan φ = (dy/dx) = ((2x)/a) ...(i),(ii) sin φ = ((x−r)/(3r)) ....(iii) tan α = tan ((π/4)−(φ/2))= (r/(y+3rcos φ)) ..(iv) ___________________________ sin φ = ((atan φ−2r)/(6r)) [using (ii) in (iii)] .....(I) using (i) in (iv) we get ((1−tan (φ/2))/(1+tan (φ/2))) = (r/(((a^2 tan^2 φ)/(4a))+3rcos φ)) ..(II) let tan (φ/2) = t in (I ) ((2t(6r))/(1+t^2 )) = ((2at)/(1+t^2 ))−2r ⇒ r(6t+1+t^2 )=at ⇒ r = ((at)/(t^2 +6t+1)) ....(III) Now considering (II) ((1−t)/(1+t)) = (r/(((at^2 )/((1+t^2 )^2 ))+3r(((1−t^2 )/(1+t^2 ))))) ⇒ (1−t)[at^2 +3r(1−t^4 )]=r(1+t)(1+t^2 )^2 ⇒ at^2 (1−t)= r[(1+t)(1+t^2 )^2 −3(1−t)(1−t^4 )] using (III) in eq. above t(1−t)(t^2 +6t+1)= (1+t)(1+t^2 )^2 −3(1−t)(1−t^4 ) From above eq. we obtain t = tan (φ/2) ≈ 0.517 tan φ = ((2t)/(1+t^2 )) ≈ 0.816 & r= ((at)/(t^2 +6t+1)) ≈ 0.1183a .](https://www.tinkutara.com/question/Q52604.png)
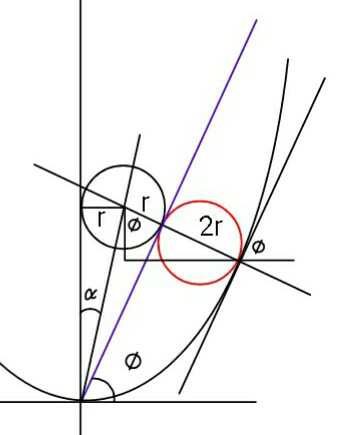
$${y}=\:\frac{{x}^{\mathrm{2}} }{{a}}\:\:\:\Rightarrow\:\:\mathrm{tan}\:\phi\:=\:\frac{{dy}}{{dx}}\:=\:\frac{\mathrm{2}{x}}{{a}}\:\:\:…\left({i}\right),\left({ii}\right) \\ $$$$\mathrm{sin}\:\phi\:=\:\frac{{x}−{r}}{\mathrm{3}{r}}\:\:\:\:\:….\left({iii}\right) \\ $$$$\mathrm{tan}\:\alpha\:=\:\mathrm{tan}\:\left(\frac{\pi}{\mathrm{4}}−\frac{\phi}{\mathrm{2}}\right)=\:\frac{{r}}{{y}+\mathrm{3}{r}\mathrm{cos}\:\phi}\:\:..\left({iv}\right) \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$$\mathrm{sin}\:\phi\:=\:\frac{{a}\mathrm{tan}\:\phi−\mathrm{2}{r}}{\mathrm{6}{r}}\:\:\:\:\left[{using}\:\left({ii}\right)\:{in}\:\left({iii}\right)\right] \\ $$$$\:\:\:…..\left({I}\right) \\ $$$${using}\:\left({i}\right)\:{in}\:\left({iv}\right)\:{we}\:{get} \\ $$$$\:\:\frac{\mathrm{1}−\mathrm{tan}\:\frac{\phi}{\mathrm{2}}}{\mathrm{1}+\mathrm{tan}\:\frac{\phi}{\mathrm{2}}}\:=\:\frac{{r}}{\frac{{a}^{\mathrm{2}} \mathrm{tan}\:^{\mathrm{2}} \phi}{\mathrm{4}{a}}+\mathrm{3}{r}\mathrm{cos}\:\phi}\:\:\:..\left({II}\right) \\ $$$${let}\:\:\mathrm{tan}\:\frac{\phi}{\mathrm{2}}\:=\:{t}\:\:{in}\:\left({I}\:\right) \\ $$$$\frac{\mathrm{2}{t}\left(\mathrm{6}{r}\right)}{\mathrm{1}+{t}^{\mathrm{2}} }\:=\:\frac{\mathrm{2}{at}}{\mathrm{1}+{t}^{\mathrm{2}} }−\mathrm{2}{r} \\ $$$$\Rightarrow\:\:{r}\left(\mathrm{6}{t}+\mathrm{1}+{t}^{\mathrm{2}} \right)={at} \\ $$$$\Rightarrow\:\:\:{r}\:=\:\frac{{at}}{{t}^{\mathrm{2}} +\mathrm{6}{t}+\mathrm{1}}\:\:\:\:\:….\left({III}\right) \\ $$$${Now}\:{considering}\:\left({II}\right) \\ $$$$\frac{\mathrm{1}−{t}}{\mathrm{1}+{t}}\:=\:\frac{{r}}{\frac{{at}^{\mathrm{2}} }{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }+\mathrm{3}{r}\left(\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }\right)} \\ $$$$\Rightarrow\:\left(\mathrm{1}−{t}\right)\left[{at}^{\mathrm{2}} +\mathrm{3}{r}\left(\mathrm{1}−{t}^{\mathrm{4}} \right)\right]={r}\left(\mathrm{1}+{t}\right)\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$$\Rightarrow \\ $$$${at}^{\mathrm{2}} \left(\mathrm{1}−{t}\right)=\:{r}\left[\left(\mathrm{1}+{t}\right)\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{3}\left(\mathrm{1}−{t}\right)\left(\mathrm{1}−{t}^{\mathrm{4}} \right)\right] \\ $$$${using}\:\left({III}\right)\:{in}\:{eq}.\:{above} \\ $$$$\boldsymbol{{t}}\left(\mathrm{1}−\boldsymbol{{t}}\right)\left(\boldsymbol{{t}}^{\mathrm{2}} +\mathrm{6}\boldsymbol{{t}}+\mathrm{1}\right)=\:\left(\mathrm{1}+\boldsymbol{{t}}\right)\left(\mathrm{1}+\boldsymbol{{t}}^{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{3}\left(\mathrm{1}−\boldsymbol{{t}}\right)\left(\mathrm{1}−\boldsymbol{{t}}^{\mathrm{4}} \right) \\ $$$${From}\:{above}\:{eq}.\:{we}\:{obtain}\: \\ $$$$\:\:\:{t}\:=\:\mathrm{tan}\:\frac{\phi}{\mathrm{2}}\:\approx\:\mathrm{0}.\mathrm{517} \\ $$$$\:\:\:\mathrm{tan}\:\phi\:=\:\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }\:\approx\:\mathrm{0}.\mathrm{816}\: \\ $$$$\:\:\:\&\:\:{r}=\:\frac{{at}}{{t}^{\mathrm{2}} +\mathrm{6}{t}+\mathrm{1}}\:\approx\:\mathrm{0}.\mathrm{1183}{a}\:. \\ $$
Commented by MJS last updated on 12/Jan/19

$$\mathrm{I}'\mathrm{m}\:\mathrm{confused}… \\ $$$$\mathrm{it}'\mathrm{s}\:\mathrm{possible}\:\mathrm{to}\:\mathrm{get}\:\mathrm{the}\:\mathrm{equations}\:\mathrm{of}\:\mathrm{2}\:\mathrm{circles} \\ $$$$\mathrm{with}\:\mathrm{radius}\:{r},\:\mathrm{having}\:\mathrm{exactly}\:\mathrm{1}\:\mathrm{common}\:\mathrm{point} \\ $$$$\mathrm{and}\:\mathrm{their}\:\mathrm{common}\:\mathrm{tangent}\:{t}:\:{y}={x}\mathrm{tan}\:\phi \\ $$$$\mathrm{it}'\mathrm{s}\:\mathrm{possible}\:\mathrm{to}\:\mathrm{find}\:\mathrm{a}\:\mathrm{parabola}\:\mathrm{having}\:\mathrm{exactly} \\ $$$$\mathrm{1}\:\mathrm{common}\:\mathrm{point}\:\mathrm{with}\:\mathrm{the}\:\mathrm{red}\:\mathrm{circle}\:\left(\mathrm{at}\:\mathrm{least}\right. \\ $$$$\left.\mathrm{approximately}\right) \\ $$$$\mathrm{but}\:\mathrm{in}\:\mathrm{general},\:\mathrm{the}\:\mathrm{common}\:\mathrm{tangent}\:\mathrm{of} \\ $$$$\mathrm{the}\:\mathrm{circle}\:\mathrm{and}\:\mathrm{the}\:\mathrm{parabola}\:\mathrm{is}\:\mathrm{not}\:\mathrm{parallel} \\ $$$$\mathrm{to}\:{y}={x}\mathrm{tan}\:\phi \\ $$
Commented by ajfour last updated on 12/Jan/19

$${when}\:{the}\:{red}\:{circle}\:{has}\:{to}\:{be}\:{of} \\ $$$${maximum}\:{radius},\:{it}\:{should}\:{be}\:{so} \\ $$$${Sir}. \\ $$
Commented by MJS last updated on 12/Jan/19
$$\mathrm{it}'\mathrm{s}\:\mathrm{just}\:\mathrm{not}\:\mathrm{obvious}\:\mathrm{to}\:\mathrm{me}…\:\mathrm{I}'\mathrm{ll}\:\mathrm{have}\:\mathrm{to}\:\mathrm{go} \\ $$$$\mathrm{through}\:\mathrm{it}… \\ $$
Answered by MJS last updated on 12/Jan/19
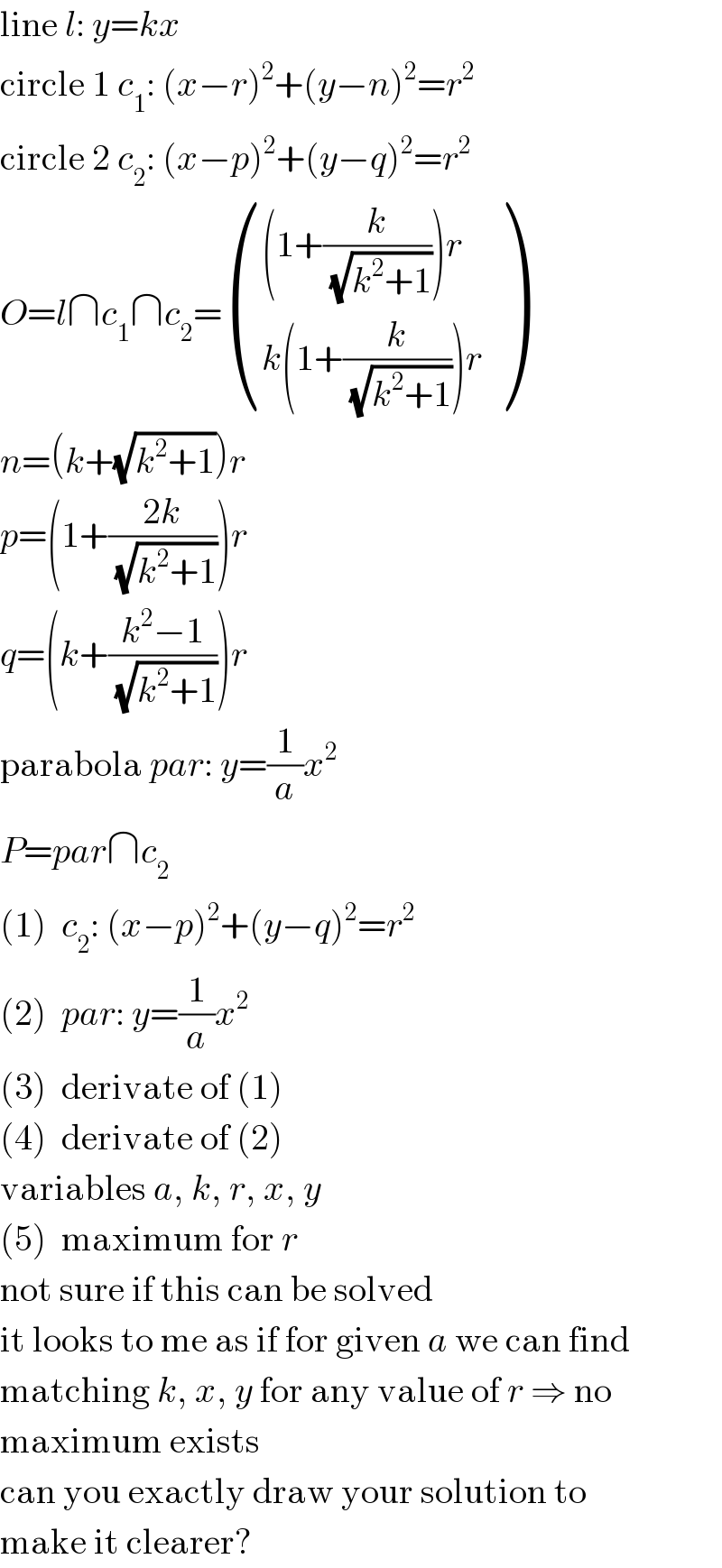
$$\mathrm{line}\:{l}:\:{y}={kx} \\ $$$$\mathrm{circle}\:\mathrm{1}\:{c}_{\mathrm{1}} :\:\left({x}−{r}\right)^{\mathrm{2}} +\left({y}−{n}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\mathrm{circle}\:\mathrm{2}\:{c}_{\mathrm{2}} :\:\left({x}−{p}\right)^{\mathrm{2}} +\left({y}−{q}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$${O}={l}\cap{c}_{\mathrm{1}} \cap{c}_{\mathrm{2}} =\begin{pmatrix}{\left(\mathrm{1}+\frac{{k}}{\:\sqrt{{k}^{\mathrm{2}} +\mathrm{1}}}\right){r}}\\{{k}\left(\mathrm{1}+\frac{{k}}{\:\sqrt{{k}^{\mathrm{2}} +\mathrm{1}}}\right){r}}\end{pmatrix} \\ $$$${n}=\left({k}+\sqrt{{k}^{\mathrm{2}} +\mathrm{1}}\right){r} \\ $$$${p}=\left(\mathrm{1}+\frac{\mathrm{2}{k}}{\:\sqrt{{k}^{\mathrm{2}} +\mathrm{1}}}\right){r} \\ $$$${q}=\left({k}+\frac{{k}^{\mathrm{2}} −\mathrm{1}}{\:\sqrt{{k}^{\mathrm{2}} +\mathrm{1}}}\right){r} \\ $$$$\mathrm{parabola}\:{par}:\:{y}=\frac{\mathrm{1}}{{a}}{x}^{\mathrm{2}} \\ $$$${P}={par}\cap{c}_{\mathrm{2}} \\ $$$$\left(\mathrm{1}\right)\:\:{c}_{\mathrm{2}} :\:\left({x}−{p}\right)^{\mathrm{2}} +\left({y}−{q}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\left(\mathrm{2}\right)\:\:{par}:\:{y}=\frac{\mathrm{1}}{{a}}{x}^{\mathrm{2}} \\ $$$$\left(\mathrm{3}\right)\:\:\mathrm{derivate}\:\mathrm{of}\:\left(\mathrm{1}\right) \\ $$$$\left(\mathrm{4}\right)\:\:\mathrm{derivate}\:\mathrm{of}\:\left(\mathrm{2}\right) \\ $$$$\mathrm{variables}\:{a},\:{k},\:{r},\:{x},\:{y} \\ $$$$\left(\mathrm{5}\right)\:\:\mathrm{maximum}\:\mathrm{for}\:{r} \\ $$$$\mathrm{not}\:\mathrm{sure}\:\mathrm{if}\:\mathrm{this}\:\mathrm{can}\:\mathrm{be}\:\mathrm{solved} \\ $$$$\mathrm{it}\:\mathrm{looks}\:\mathrm{to}\:\mathrm{me}\:\mathrm{as}\:\mathrm{if}\:\mathrm{for}\:\mathrm{given}\:{a}\:\mathrm{we}\:\mathrm{can}\:\mathrm{find} \\ $$$$\mathrm{matching}\:{k},\:{x},\:{y}\:\mathrm{for}\:\mathrm{any}\:\mathrm{value}\:\mathrm{of}\:{r}\:\Rightarrow\:\mathrm{no} \\ $$$$\mathrm{maximum}\:\mathrm{exists} \\ $$$$\mathrm{can}\:\mathrm{you}\:\mathrm{exactly}\:\mathrm{draw}\:\mathrm{your}\:\mathrm{solution}\:\mathrm{to} \\ $$$$\mathrm{make}\:\mathrm{it}\:\mathrm{clearer}? \\ $$
Commented by MJS last updated on 12/Jan/19

$$\mathrm{imagine}\:\mathrm{the}\:\mathrm{following}\:\mathrm{steps} \\ $$$$\mathrm{1}.\:\mathrm{draw}\:{y}=\frac{\mathrm{1}}{{a}}{x}^{\mathrm{2}} \\ $$$$\mathrm{2}.\:\mathrm{fix}\:\mathrm{a}\:\mathrm{pole}\:\mathrm{at}\:\mathrm{origin},\:\mathrm{attach}\:\mathrm{2}\:\mathrm{circles}\:\mathrm{with} \\ $$$$\mathrm{any}\:\mathrm{radius} \\ $$$$\mathrm{3}.\:\mathrm{slide}\:\mathrm{up}\:\mathrm{the}\:\mathrm{circles}\:\mathrm{along}\:\mathrm{the}\:\mathrm{pole},\:\mathrm{the} \\ $$$$\mathrm{left}\:\mathrm{handed}\:\mathrm{circle}\:\mathrm{along}\:\mathrm{the}\:{y}−\mathrm{axis} \\ $$$$\Rightarrow\:\mathrm{at}\:\mathrm{some}\:\mathrm{distance}\:\mathrm{the}\:\mathrm{right}\:\mathrm{handed}\:\mathrm{circle} \\ $$$$\mathrm{will}\:\mathrm{intersect}\:\mathrm{the}\:\mathrm{parabola}\:\mathrm{in}\:\mathrm{exactly}\:\mathrm{1}\:\mathrm{point} \\ $$$$\mathrm{why}\:\mathrm{should}\:\mathrm{there}\:\mathrm{be}\:\mathrm{an}\:\mathrm{upper}\:\mathrm{limit}\:\mathrm{for}\:{r}? \\ $$
Commented by ajfour last updated on 13/Jan/19

$${you}\:{have}\:{a}\:{Genuine}\:{objection}\:{Sir}. \\ $$
