Question Number 52611 by ajfour last updated on 10/Jan/19

Commented by ajfour last updated on 11/Jan/19
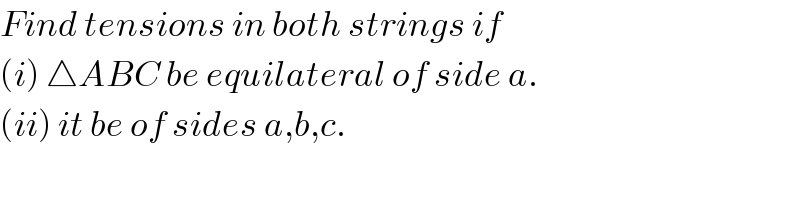
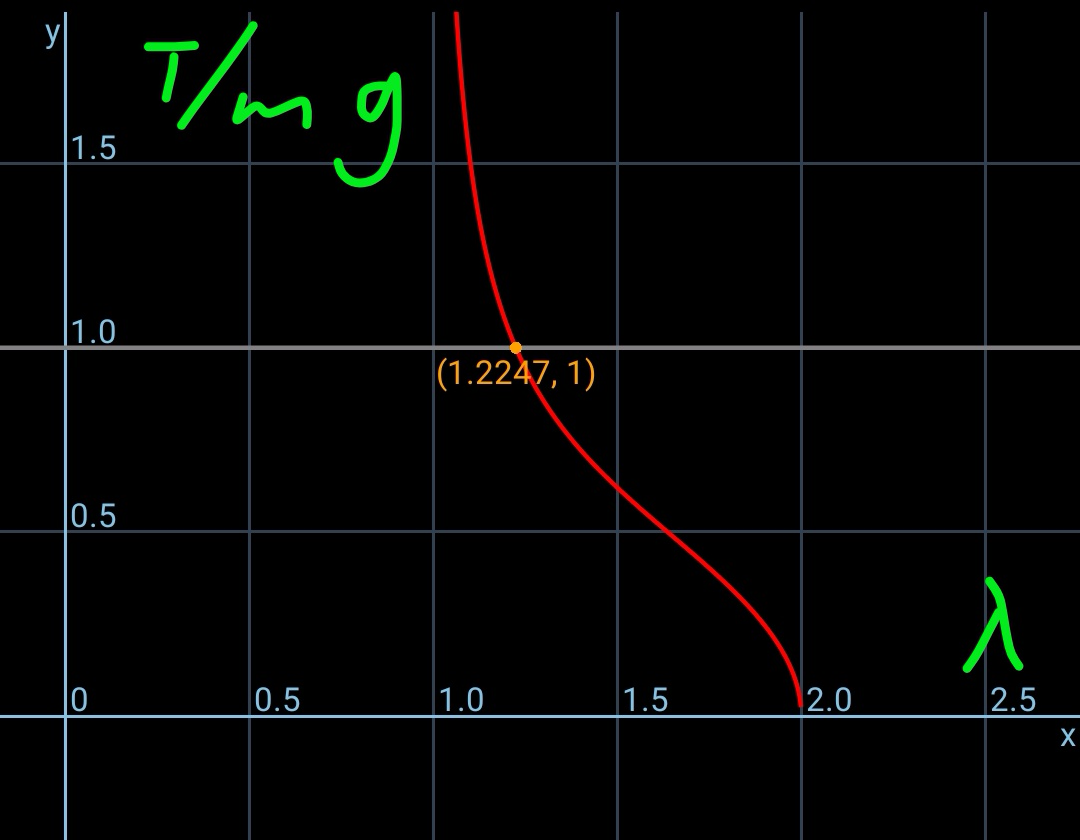
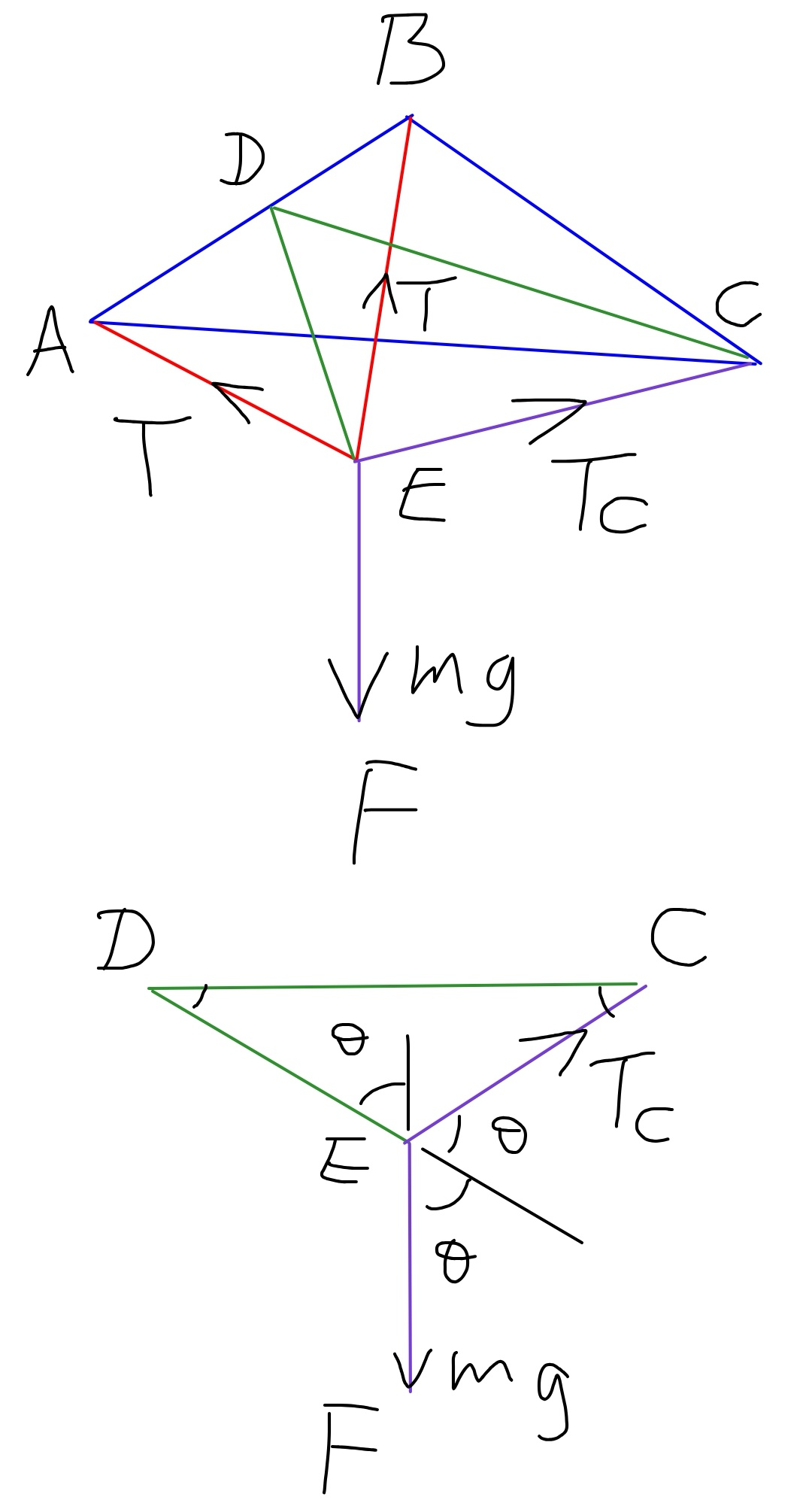
$${Find}\:{tensions}\:{in}\:{both}\:{strings}\:{if} \\ $$$$\left({i}\right)\:\bigtriangleup{ABC}\:{be}\:{equilateral}\:{of}\:{side}\:{a}. \\ $$$$\left({ii}\right)\:{it}\:{be}\:{of}\:{sides}\:{a},{b},{c}.\:\: \\ $$
Commented by ajfour last updated on 11/Jan/19

$${mrW}\:{Sir},\:{can}\:{you}\:{help}\:{me}\:{find} \\ $$$${your}\:{question}\:{in}\:{which}\:{i}\:{had}\:{found} \\ $$$${height}\:{of}\:{vertex}\:{of}\:{pyramid}\:{with} \\ $$$${lateral}\:{edges}\:{p},{q},{r}\:{and}\:{sides}\:{of}\:{base} \\ $$$${a},{b},{c}\:?\: \\ $$
Commented by mr W last updated on 12/Jan/19

$${see}\:{Q}\mathrm{47145},\:{Q}\mathrm{47113} \\ $$
Commented by mr W last updated on 12/Jan/19
$${thanks}\:{for}\:{checking}\:{sir}! \\ $$
Commented by ajfour last updated on 12/Jan/19
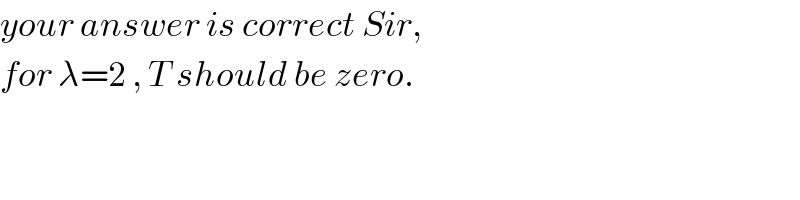
$${your}\:{answer}\:{is}\:{correct}\:{Sir}, \\ $$$${for}\:\lambda=\mathrm{2}\:,\:{T}\:{should}\:{be}\:{zero}. \\ $$
Answered by mr W last updated on 12/Jan/19
Commented by ajfour last updated on 12/Jan/19
$${Exceptionally}\:{good}\:{Sir},\:\mathcal{SUPERB}\:! \\ $$
Commented by mr W last updated on 13/Jan/19
![the general case with different side lengthes can also be solved in the same way as here, but very lengthy. so only the case with equilateral triangle is treated. AB=BC=CA=a AE=BE=l/2 let λ=(l/a) CD=(((√3)a)/2) DE=(√(((l/2))^2 −((a/2))^2 ))=((√(l^2 −a^2 ))/2) in triangle ΔDEC: ∠D=(π/2)−θ ∠DEC=π−θ ∠DCE=θ−((π/2)−θ)=2θ−(π/2) (((√3)a)/(2 sin (π−θ)))=((√(l^2 −a^2 ))/(2 sin (2θ−(π/2)))) ⇒((√3)/(sin θ))=((√(λ^2 −1))/(−cos 2θ)) ⇒((√3)/(sin θ))=((√(λ^2 −1))/(2 sin^2 θ−1)) ⇒2(√3) sin^2 θ−(√(λ^2 −1)) sin θ−(√3)=0 ⇒sin θ=(((√(λ^2 −1))+(√(λ^2 +23)))/(4(√3))) ⇒cos θ=((√(2[13−λ^2 −(√((λ^2 −1)(λ^2 +23)))]))/(4(√3))) T_(DE) =2T((√(l^2 −a^2 ))/l)=2T((√(λ^2 −1))/λ) T_(DE) =2mg cos θ ⇒T=mg×((λ cos θ)/( (√(λ^2 −1))))=((mgλ(√(2[13−λ^2 −(√((λ^2 −1)(λ^2 +23)))])))/(4(√(3(λ^2 −1))))) ⇒T=mg(λ/4)(√((2[13−λ^2 −(√((λ^2 −1)(λ^2 +23)))])/(3(λ^2 −1)))) it′s obvious that a<l≤2a, i.e. 1<λ≤2.](https://www.tinkutara.com/question/Q52772.png)
$${the}\:{general}\:{case}\:{with}\:{different}\:{side} \\ $$$${lengthes}\:{can}\:{also}\:{be}\:{solved}\:{in}\:{the} \\ $$$${same}\:{way}\:{as}\:{here},\:{but}\:{very}\:{lengthy}. \\ $$$${so}\:{only}\:{the}\:{case}\:{with}\:{equilateral} \\ $$$${triangle}\:{is}\:{treated}. \\ $$$${AB}={BC}={CA}={a} \\ $$$${AE}={BE}={l}/\mathrm{2} \\ $$$${let}\:\lambda=\frac{{l}}{{a}} \\ $$$${CD}=\frac{\sqrt{\mathrm{3}}{a}}{\mathrm{2}} \\ $$$${DE}=\sqrt{\left(\frac{{l}}{\mathrm{2}}\right)^{\mathrm{2}} −\left(\frac{{a}}{\mathrm{2}}\right)^{\mathrm{2}} }=\frac{\sqrt{{l}^{\mathrm{2}} −{a}^{\mathrm{2}} }}{\mathrm{2}} \\ $$$${in}\:{triangle}\:\Delta{DEC}: \\ $$$$\angle{D}=\frac{\pi}{\mathrm{2}}−\theta \\ $$$$\angle{DEC}=\pi−\theta \\ $$$$\angle{DCE}=\theta−\left(\frac{\pi}{\mathrm{2}}−\theta\right)=\mathrm{2}\theta−\frac{\pi}{\mathrm{2}} \\ $$$$\frac{\sqrt{\mathrm{3}}{a}}{\mathrm{2}\:\mathrm{sin}\:\left(\pi−\theta\right)}=\frac{\sqrt{{l}^{\mathrm{2}} −{a}^{\mathrm{2}} }}{\mathrm{2}\:\mathrm{sin}\:\left(\mathrm{2}\theta−\frac{\pi}{\mathrm{2}}\right)} \\ $$$$\Rightarrow\frac{\sqrt{\mathrm{3}}}{\mathrm{sin}\:\theta}=\frac{\sqrt{\lambda^{\mathrm{2}} −\mathrm{1}}}{−\mathrm{cos}\:\mathrm{2}\theta} \\ $$$$\Rightarrow\frac{\sqrt{\mathrm{3}}}{\mathrm{sin}\:\theta}=\frac{\sqrt{\lambda^{\mathrm{2}} −\mathrm{1}}}{\mathrm{2}\:\mathrm{sin}^{\mathrm{2}} \:\theta−\mathrm{1}} \\ $$$$\Rightarrow\mathrm{2}\sqrt{\mathrm{3}}\:\mathrm{sin}^{\mathrm{2}} \:\theta−\sqrt{\lambda^{\mathrm{2}} −\mathrm{1}}\:\mathrm{sin}\:\theta−\sqrt{\mathrm{3}}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{sin}\:\theta=\frac{\sqrt{\lambda^{\mathrm{2}} −\mathrm{1}}+\sqrt{\lambda^{\mathrm{2}} +\mathrm{23}}}{\mathrm{4}\sqrt{\mathrm{3}}} \\ $$$$\Rightarrow\mathrm{cos}\:\theta=\frac{\sqrt{\mathrm{2}\left[\mathrm{13}−\lambda^{\mathrm{2}} −\sqrt{\left(\lambda^{\mathrm{2}} −\mathrm{1}\right)\left(\lambda^{\mathrm{2}} +\mathrm{23}\right)}\right]}}{\mathrm{4}\sqrt{\mathrm{3}}} \\ $$$${T}_{{DE}} =\mathrm{2}{T}\frac{\sqrt{{l}^{\mathrm{2}} −{a}^{\mathrm{2}} }}{{l}}=\mathrm{2}{T}\frac{\sqrt{\lambda^{\mathrm{2}} −\mathrm{1}}}{\lambda} \\ $$$${T}_{{DE}} =\mathrm{2}{mg}\:\mathrm{cos}\:\theta \\ $$$$\Rightarrow{T}={mg}×\frac{\lambda\:\mathrm{cos}\:\theta}{\:\sqrt{\lambda^{\mathrm{2}} −\mathrm{1}}}=\frac{{mg}\lambda\sqrt{\mathrm{2}\left[\mathrm{13}−\lambda^{\mathrm{2}} −\sqrt{\left(\lambda^{\mathrm{2}} −\mathrm{1}\right)\left(\lambda^{\mathrm{2}} +\mathrm{23}\right)}\right]}}{\mathrm{4}\sqrt{\mathrm{3}\left(\lambda^{\mathrm{2}} −\mathrm{1}\right)}} \\ $$$$\Rightarrow{T}={mg}\frac{\lambda}{\mathrm{4}}\sqrt{\frac{\mathrm{2}\left[\mathrm{13}−\lambda^{\mathrm{2}} −\sqrt{\left(\lambda^{\mathrm{2}} −\mathrm{1}\right)\left(\lambda^{\mathrm{2}} +\mathrm{23}\right)}\right]}{\mathrm{3}\left(\lambda^{\mathrm{2}} −\mathrm{1}\right)}} \\ $$$${it}'{s}\:{obvious}\:{that}\:{a}<{l}\leqslant\mathrm{2}{a},\:{i}.{e}.\:\mathrm{1}<\lambda\leqslant\mathrm{2}. \\ $$
Commented by mr W last updated on 12/Jan/19