Menu Close

Question-52663

Tinku Tara 0 Comments
Pin




Question Number 52663 by ajfour last updated on 11/Jan/19
Commented by ajfour last updated on 11/Jan/19
Find radius R in terms of a and b. Also find the central area in yellow in terms of a and b. (source: ajfour)
$${Find}\:{radius}\:{R}\:{in}\:{terms}\:{of}\:{a}\:{and}\:{b}. \\ $$$${Also}\:{find}\:{the}\:{central}\:{area}\:{in}\:{yellow} \\ $$$${in}\:{terms}\:{of}\:{a}\:{and}\:{b}.\:\:\left({source}:\:{ajfour}\right) \\ $$
Answered by mr W last updated on 11/Jan/19
(a^2 −r^2 )+(b^2 −r^2 )=((√(a^2 −r^2 ))−r+(√(b^2 −r^2 ))−r)^2 a^2 +b^2 −2r^2 =((√(a^2 −r^2 ))+(√(b^2 −r^2 ))−2r)^2 a^2 +b^2 −2r^2 =a^2 −r^2 +b^2 −r^2 +4r^2 +2[(√((a^2 −r^2 )(b^2 −r^2 )))−2r((√(a^2 −r^2 ))+(√(b^2 −r^2 )))] ⇒(√((a^2 −r^2 )(b^2 −r^2 )))=2r((√(a^2 −r^2 ))+(√(b^2 −r^2 ))−r) example: a=3, b=4⇒r=0.9569
$$\left({a}^{\mathrm{2}} −{r}^{\mathrm{2}} \right)+\left({b}^{\mathrm{2}} −{r}^{\mathrm{2}} \right)=\left(\sqrt{{a}^{\mathrm{2}} −{r}^{\mathrm{2}} }−{r}+\sqrt{{b}^{\mathrm{2}} −{r}^{\mathrm{2}} }−{r}\right)^{\mathrm{2}} \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{r}^{\mathrm{2}} =\left(\sqrt{{a}^{\mathrm{2}} −{r}^{\mathrm{2}} }+\sqrt{{b}^{\mathrm{2}} −{r}^{\mathrm{2}} }−\mathrm{2}{r}\right)^{\mathrm{2}} \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{r}^{\mathrm{2}} ={a}^{\mathrm{2}} −{r}^{\mathrm{2}} +{b}^{\mathrm{2}} −{r}^{\mathrm{2}} +\mathrm{4}{r}^{\mathrm{2}} +\mathrm{2}\left[\sqrt{\left({a}^{\mathrm{2}} −{r}^{\mathrm{2}} \right)\left({b}^{\mathrm{2}} −{r}^{\mathrm{2}} \right)}−\mathrm{2}{r}\left(\sqrt{{a}^{\mathrm{2}} −{r}^{\mathrm{2}} }+\sqrt{{b}^{\mathrm{2}} −{r}^{\mathrm{2}} }\right)\right] \\ $$$$\Rightarrow\sqrt{\left({a}^{\mathrm{2}} −{r}^{\mathrm{2}} \right)\left({b}^{\mathrm{2}} −{r}^{\mathrm{2}} \right)}=\mathrm{2}{r}\left(\sqrt{{a}^{\mathrm{2}} −{r}^{\mathrm{2}} }+\sqrt{{b}^{\mathrm{2}} −{r}^{\mathrm{2}} }−{r}\right) \\ $$$${example}: \\ $$$${a}=\mathrm{3},\:{b}=\mathrm{4}\Rightarrow{r}=\mathrm{0}.\mathrm{9569} \\ $$
Commented by ajfour last updated on 11/Jan/19
cant we have R in terms of a and b Sir? i′ve proceeded to some length, shall post soon, thanks afterall.
$${cant}\:{we}\:{have}\:{R}\:{in}\:{terms}\:{of}\:{a}\:{and}\:{b} \\ $$$${Sir}?\:{i}'{ve}\:{proceeded}\:{to}\:{some}\:{length}, \\ $$$${shall}\:{post}\:{soon},\:{thanks}\:{afterall}. \\ $$
Answered by ajfour last updated on 18/Jan/19
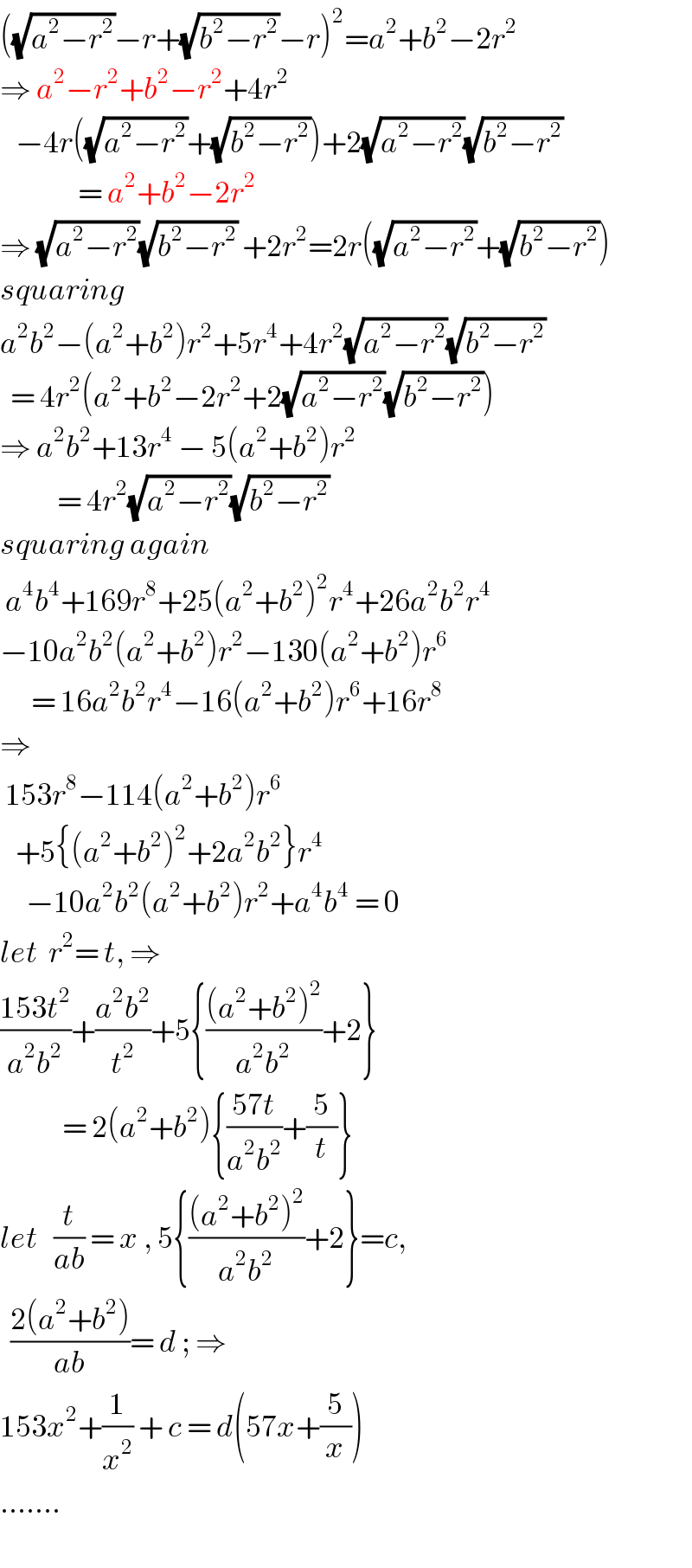
((√(a^2 −r^2 ))−r+(√(b^2 −r^2 ))−r)^2 =a^2 +b^2 −2r^2 ⇒ a^2 −r^2 +b^2 −r^2 +4r^2 −4r((√(a^2 −r^2 ))+(√(b^2 −r^2 )))+2(√(a^2 −r^2 ))(√(b^2 −r^2 )) = a^2 +b^2 −2r^2 ⇒ (√(a^2 −r^2 ))(√(b^2 −r^2 )) +2r^2 =2r((√(a^2 −r^2 ))+(√(b^2 −r^2 ))) squaring a^2 b^2 −(a^2 +b^2 )r^2 +5r^4 +4r^2 (√(a^2 −r^2 ))(√(b^2 −r^2 )) = 4r^2 (a^2 +b^2 −2r^2 +2(√(a^2 −r^2 ))(√(b^2 −r^2 ))) ⇒ a^2 b^2 +13r^4 − 5(a^2 +b^2 )r^2 = 4r^2 (√(a^2 −r^2 ))(√(b^2 −r^2 )) squaring again a^4 b^4 +169r^8 +25(a^2 +b^2 )^2 r^4 +26a^2 b^2 r^4 −10a^2 b^2 (a^2 +b^2 )r^2 −130(a^2 +b^2 )r^6 = 16a^2 b^2 r^4 −16(a^2 +b^2 )r^6 +16r^8 ⇒ 153r^8 −114(a^2 +b^2 )r^6 +5{(a^2 +b^2 )^2 +2a^2 b^2 }r^4 −10a^2 b^2 (a^2 +b^2 )r^2 +a^4 b^4 = 0 let r^2 = t, ⇒ ((153t^2 )/(a^2 b^2 ))+((a^2 b^2 )/t^2 )+5{(((a^2 +b^2 )^2 )/(a^2 b^2 ))+2} = 2(a^2 +b^2 ){((57t)/(a^2 b^2 ))+(5/t)} let (t/(ab)) = x , 5{(((a^2 +b^2 )^2 )/(a^2 b^2 ))+2}=c, ((2(a^2 +b^2 ))/(ab))= d ; ⇒ 153x^2 +(1/x^2 ) + c = d(57x+(5/x)) .......
$$\left(\sqrt{{a}^{\mathrm{2}} −{r}^{\mathrm{2}} }−{r}+\sqrt{{b}^{\mathrm{2}} −{r}^{\mathrm{2}} }−{r}\right)^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{r}^{\mathrm{2}} \\ $$$$\Rightarrow\:{a}^{\mathrm{2}} −{r}^{\mathrm{2}} +{b}^{\mathrm{2}} −{r}^{\mathrm{2}} +\mathrm{4}{r}^{\mathrm{2}} \\ $$$$\:\:\:−\mathrm{4}{r}\left(\sqrt{{a}^{\mathrm{2}} −{r}^{\mathrm{2}} }+\sqrt{{b}^{\mathrm{2}} −{r}^{\mathrm{2}} }\right)+\mathrm{2}\sqrt{{a}^{\mathrm{2}} −{r}^{\mathrm{2}} }\sqrt{{b}^{\mathrm{2}} −{r}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{r}^{\mathrm{2}} \\ $$$$\Rightarrow\:\sqrt{{a}^{\mathrm{2}} −{r}^{\mathrm{2}} }\sqrt{{b}^{\mathrm{2}} −{r}^{\mathrm{2}} }\:+\mathrm{2}{r}^{\mathrm{2}} =\mathrm{2}{r}\left(\sqrt{{a}^{\mathrm{2}} −{r}^{\mathrm{2}} }+\sqrt{{b}^{\mathrm{2}} −{r}^{\mathrm{2}} }\right) \\ $$$${squaring} \\ $$$${a}^{\mathrm{2}} {b}^{\mathrm{2}} −\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right){r}^{\mathrm{2}} +\mathrm{5}{r}^{\mathrm{4}} +\mathrm{4}{r}^{\mathrm{2}} \sqrt{{a}^{\mathrm{2}} −{r}^{\mathrm{2}} }\sqrt{{b}^{\mathrm{2}} −{r}^{\mathrm{2}} } \\ $$$$\:\:=\:\mathrm{4}{r}^{\mathrm{2}} \left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{r}^{\mathrm{2}} +\mathrm{2}\sqrt{{a}^{\mathrm{2}} −{r}^{\mathrm{2}} }\sqrt{{b}^{\mathrm{2}} −{r}^{\mathrm{2}} }\right) \\ $$$$\Rightarrow\:{a}^{\mathrm{2}} {b}^{\mathrm{2}} +\mathrm{13}{r}^{\mathrm{4}} \:−\:\mathrm{5}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right){r}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{4}{r}^{\mathrm{2}} \sqrt{{a}^{\mathrm{2}} −{r}^{\mathrm{2}} }\sqrt{{b}^{\mathrm{2}} −{r}^{\mathrm{2}} } \\ $$$${squaring}\:{again} \\ $$$$\:{a}^{\mathrm{4}} {b}^{\mathrm{4}} +\mathrm{169}{r}^{\mathrm{8}} +\mathrm{25}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)^{\mathrm{2}} {r}^{\mathrm{4}} +\mathrm{26}{a}^{\mathrm{2}} {b}^{\mathrm{2}} {r}^{\mathrm{4}} \\ $$$$−\mathrm{10}{a}^{\mathrm{2}} {b}^{\mathrm{2}} \left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right){r}^{\mathrm{2}} −\mathrm{130}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right){r}^{\mathrm{6}} \\ $$$$\:\:\:\:\:\:=\:\mathrm{16}{a}^{\mathrm{2}} {b}^{\mathrm{2}} {r}^{\mathrm{4}} −\mathrm{16}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right){r}^{\mathrm{6}} +\mathrm{16}{r}^{\mathrm{8}} \\ $$$$\Rightarrow \\ $$$$\:\mathrm{153}{r}^{\mathrm{8}} −\mathrm{114}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right){r}^{\mathrm{6}} \\ $$$$\:\:\:+\mathrm{5}\left\{\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)^{\mathrm{2}} +\mathrm{2}{a}^{\mathrm{2}} {b}^{\mathrm{2}} \right\}{r}^{\mathrm{4}} \\ $$$$\:\:\:\:\:−\mathrm{10}{a}^{\mathrm{2}} {b}^{\mathrm{2}} \left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right){r}^{\mathrm{2}} +{a}^{\mathrm{4}} {b}^{\mathrm{4}} \:=\:\mathrm{0} \\ $$$${let}\:\:{r}^{\mathrm{2}} =\:{t},\:\Rightarrow \\ $$$$\frac{\mathrm{153}{t}^{\mathrm{2}} }{{a}^{\mathrm{2}} {b}^{\mathrm{2}} }+\frac{{a}^{\mathrm{2}} {b}^{\mathrm{2}} }{{t}^{\mathrm{2}} }+\mathrm{5}\left\{\frac{\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)^{\mathrm{2}} }{{a}^{\mathrm{2}} {b}^{\mathrm{2}} }+\mathrm{2}\right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)\left\{\frac{\mathrm{57}{t}}{{a}^{\mathrm{2}} {b}^{\mathrm{2}} }+\frac{\mathrm{5}}{{t}}\right\} \\ $$$${let}\:\:\:\frac{{t}}{{ab}}\:=\:{x}\:,\:\mathrm{5}\left\{\frac{\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)^{\mathrm{2}} }{{a}^{\mathrm{2}} {b}^{\mathrm{2}} }+\mathrm{2}\right\}={c}, \\ $$$$\:\:\frac{\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)}{{ab}}=\:{d}\:;\:\Rightarrow \\ $$$$\mathrm{153}{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:+\:{c}\:=\:{d}\left(\mathrm{57}{x}+\frac{\mathrm{5}}{{x}}\right) \\ $$$$……. \\ $$
Commented by ajfour last updated on 11/Jan/19
yes sir, not useful etal..
$${yes}\:{sir},\:{not}\:{useful}\:{etal}.. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *