Question Number 52780 by ajfour last updated on 12/Jan/19
Commented by ajfour last updated on 13/Jan/19
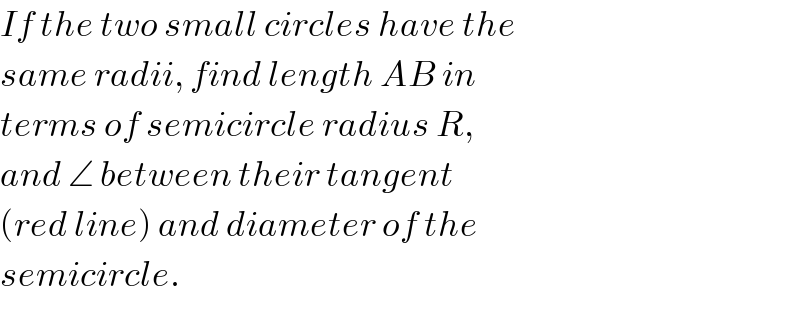
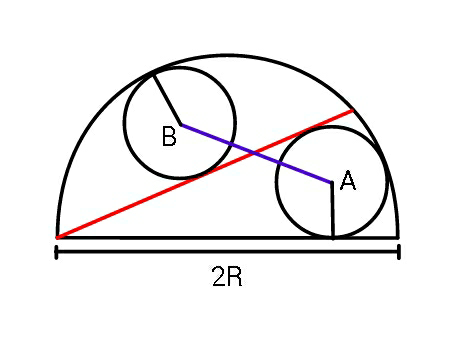
$${If}\:{the}\:{two}\:{small}\:{circles}\:{have}\:{the} \\ $$$${same}\:{radii},\:{find}\:{length}\:{AB}\:{in} \\ $$$${terms}\:{of}\:{semicircle}\:{radius}\:{R}, \\ $$$${and}\:\angle\:{between}\:{their}\:{tangent}\: \\ $$$$\left({red}\:{line}\right)\:{and}\:{diameter}\:{of}\:{the} \\ $$$${semicircle}.\:\:\: \\ $$
Answered by mr W last updated on 13/Jan/19
Commented by mr W last updated on 13/Jan/19
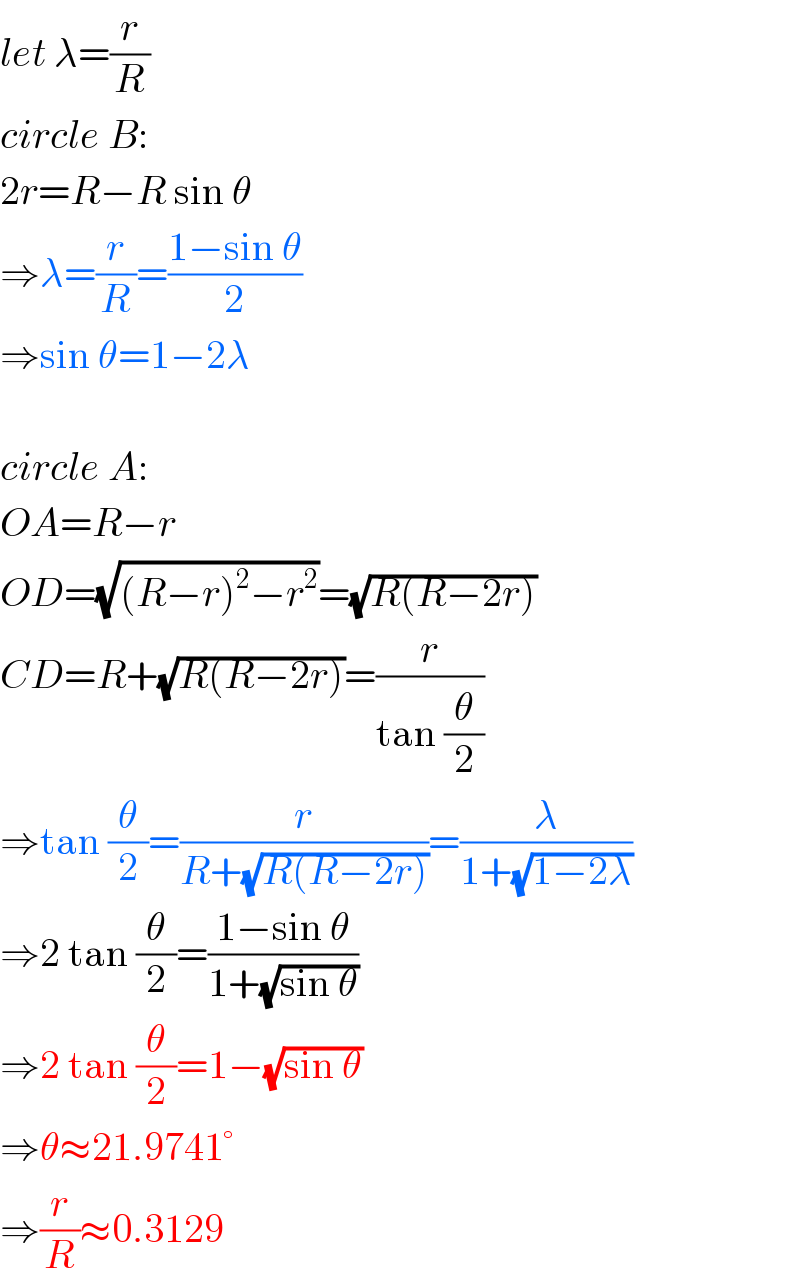
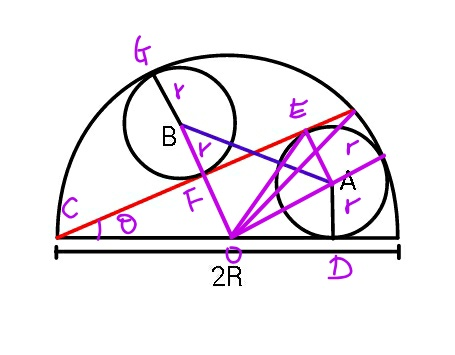
$${let}\:\lambda=\frac{{r}}{{R}} \\ $$$${circle}\:{B}: \\ $$$$\mathrm{2}{r}={R}−{R}\:\mathrm{sin}\:\theta \\ $$$$\Rightarrow\lambda=\frac{{r}}{{R}}=\frac{\mathrm{1}−\mathrm{sin}\:\theta}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{sin}\:\theta=\mathrm{1}−\mathrm{2}\lambda \\ $$$$ \\ $$$${circle}\:{A}: \\ $$$${OA}={R}−{r} \\ $$$${OD}=\sqrt{\left({R}−{r}\right)^{\mathrm{2}} −{r}^{\mathrm{2}} }=\sqrt{{R}\left({R}−\mathrm{2}{r}\right)} \\ $$$${CD}={R}+\sqrt{{R}\left({R}−\mathrm{2}{r}\right)}=\frac{{r}}{\mathrm{tan}\:\frac{\theta}{\mathrm{2}}} \\ $$$$\Rightarrow\mathrm{tan}\:\frac{\theta}{\mathrm{2}}=\frac{{r}}{{R}+\sqrt{{R}\left({R}−\mathrm{2}{r}\right)}}=\frac{\lambda}{\mathrm{1}+\sqrt{\mathrm{1}−\mathrm{2}\lambda}} \\ $$$$\Rightarrow\mathrm{2}\:\mathrm{tan}\:\frac{\theta}{\mathrm{2}}=\frac{\mathrm{1}−\mathrm{sin}\:\theta}{\mathrm{1}+\sqrt{\mathrm{sin}\:\theta}} \\ $$$$\Rightarrow\mathrm{2}\:\mathrm{tan}\:\frac{\theta}{\mathrm{2}}=\mathrm{1}−\sqrt{\mathrm{sin}\:\theta} \\ $$$$\Rightarrow\theta\approx\mathrm{21}.\mathrm{9741}° \\ $$$$\Rightarrow\frac{{r}}{{R}}\approx\mathrm{0}.\mathrm{3129} \\ $$
Commented by ajfour last updated on 13/Jan/19
$${Nice}\:{Way}\:{Sir}!\:{Thank}\:{you}. \\ $$
Commented by Otchere Abdullai last updated on 13/Jan/19
$${we}\:{thank}\:{God}\:{for}\:{such}\:{a}\:{wonderful}\: \\ $$$${man}! \\ $$
