Question Number 52814 by ajfour last updated on 13/Jan/19
Commented by ajfour last updated on 13/Jan/19

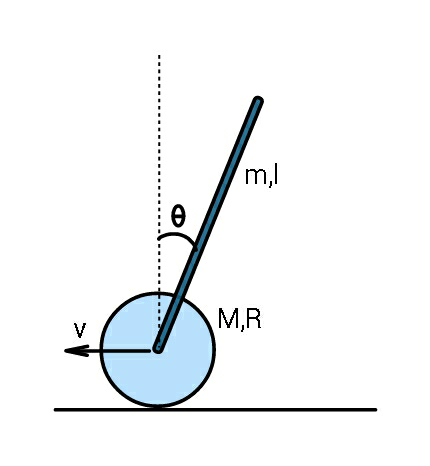
$${Initially}\:{rod}\:{whose}\:{one}\:{end}\:{is} \\ $$$${pivoted}\:{to}\:{centre}\:{of}\:{disc},\:{is}\:{kept} \\ $$$${vertical}\:{and}\:{released},\:{Find}\:{v}\left(\theta\right). \\ $$$${Friction}\:{is}\:{sufficient}\:{say},\: \\ $$$${coefficient}\:{is}\:\mu. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 13/Jan/19

$${mg}×\frac{{l}}{\mathrm{2}}\left(\mathrm{1}−{cos}\theta\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{{ml}^{\mathrm{2}} }{\mathrm{3}}\right)\left({w}_{{rod}} \right)^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}{mV}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}{MV}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{2}}{MR}^{\mathrm{2}} \right)\left({w}_{{disc}} \right)^{\mathrm{2}} \\ $$$${above}\:{eqn}\:\:{loss}\:{o}\:{P}.{E}={k}.{E}\:\left({rotational}+{liniear}\:\right){for}\:{both}\:{disc}\:{and}\:{rod} \\ $$$$ \\ $$$$\left(\frac{{ml}^{\mathrm{2}} }{\mathrm{3}}\right){w}_{{rod}} =\left(\frac{\mathrm{1}}{\mathrm{2}}{MR}^{\mathrm{2}} \right){w}_{{disc}} \leftarrow{conservation}\:{of}\:{angular}\:{momentum} \\ $$$$\left(\frac{{ml}^{\mathrm{2}} }{\mathrm{3}}\right){w}_{{rod}} =\left(\frac{{MR}^{\mathrm{2}} }{\mathrm{2}}\right)\left(\frac{{V}}{{R}}\right) \\ $$$${w}_{{rod}} =\frac{{MR}^{\mathrm{2}} ×\mathrm{3}}{\mathrm{2}×{ml}^{\mathrm{2}} }×\frac{{V}}{{R}} \\ $$$${w}_{{rod}} =\frac{\mathrm{3}{M}}{\mathrm{2}{m}}×\left(\frac{{RV}}{{l}^{\mathrm{2}} }\right) \\ $$$${mg}×\frac{{l}}{\mathrm{2}}\left(\mathrm{1}−{cos}\theta\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{{ml}^{\mathrm{2}} }{\mathrm{3}}\right)\left(\frac{\mathrm{9}{M}^{\mathrm{2}} }{\mathrm{4}{m}^{\mathrm{2}} }×\frac{{R}^{\mathrm{2}} {V}^{\mathrm{2}} }{{l}^{\mathrm{4}} }\right)+\frac{\mathrm{1}}{\mathrm{2}}{mV}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}{MV}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{2}}{MR}^{\mathrm{2}} \right)\left(\frac{{V}^{\mathrm{2}} }{{R}^{\mathrm{2}} }\right) \\ $$$${mg}×\frac{{l}}{\mathrm{2}}\left(\mathrm{1}−{cos}\theta\right)=\frac{\mathrm{3}}{\mathrm{8}}\left(\frac{{M}^{\mathrm{2}} }{{m}}\right)\left(\frac{{R}^{\mathrm{2}} }{{l}^{\mathrm{2}} }\right){V}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}{MV}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{4}}{MV}^{\mathrm{2}} \\ $$$$=\frac{\mathrm{3}}{\mathrm{8}}\left(\frac{{M}^{\mathrm{2}} }{{m}}\right)\left(\frac{{R}^{\mathrm{2}} }{{l}^{\mathrm{2}} }\right){V}^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}{MV}^{\mathrm{2}} \\ $$$$=\frac{\mathrm{3}}{\mathrm{4}}{MV}^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}×\frac{{M}}{{m}}×\frac{{R}^{\mathrm{2}} }{{l}^{\mathrm{2}} }\right) \\ $$$${V}^{\mathrm{2}} =\frac{{mgl}\left(\mathrm{1}−{cos}\theta\right)}{\mathrm{2}×\frac{\mathrm{3}}{\mathrm{4}}{M}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}×\frac{{M}}{{m}}×\frac{{R}^{\mathrm{2}} }{{l}^{\mathrm{2}} }\right)} \\ $$$${V}^{\mathrm{2}} =\frac{\mathrm{2}{mgl}\left(\mathrm{1}−{cos}\theta\right)}{\mathrm{3}{M}\left(\mathrm{1}+\frac{{MR}^{\mathrm{2}} }{\mathrm{2}{ml}^{\mathrm{2}} }\right)} \\ $$$${is}\:{it}\:{ok}… \\ $$$$ \\ $$
Commented by ajfour last updated on 13/Jan/19
$${i}\:{shall}\:{go}\:{through}\:{sir},\:{let}\:{some}\:{time}.. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 13/Jan/19

$${ok}\:{sir} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 14/Jan/19

$${ok}\:{sir}… \\ $$
Commented by ajfour last updated on 14/Jan/19

$${Tanmay}\:{Sir},\:{i}\:{think}\:{in}\:{conservation} \\ $$$${of}\:{angular}\:{momentum}\:{we}\:{should} \\ $$$${also}\:{include}\:\:{MVR}.. \\ $$
