Question Number 52825 by ajfour last updated on 13/Jan/19
Commented by ajfour last updated on 13/Jan/19
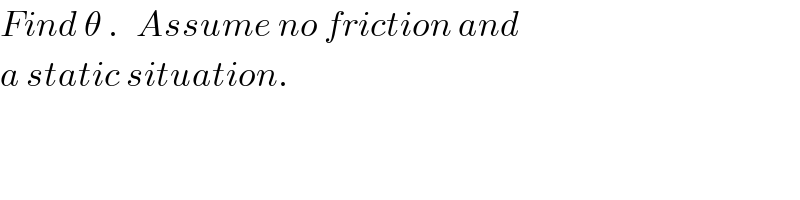
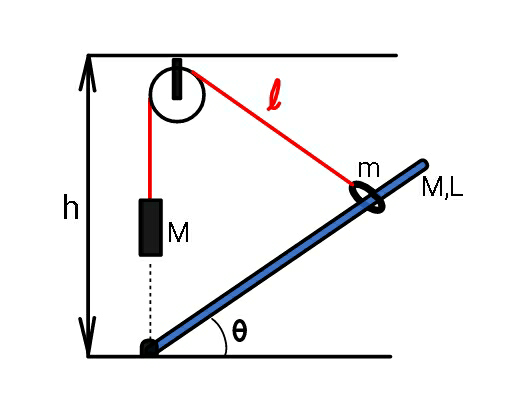
$${Find}\:\theta\:.\:\:\:{Assume}\:{no}\:{friction}\:{and} \\ $$$${a}\:{static}\:{situation}. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 13/Jan/19
Commented by ajfour last updated on 14/Jan/19
Commented by mr W last updated on 14/Jan/19
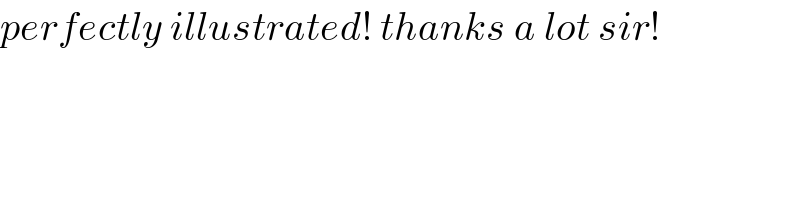
$${perfectly}\:{illustrated}!\:{thanks}\:{a}\:{lot}\:{sir}! \\ $$
Answered by mr W last updated on 14/Jan/19
![let η=(m/M), λ=(L/h) α=angle between string and vertical a=distance from ring to lower end of rod N=contact force between ring and rod ((MgL cos θ)/2)=Na ((Mg)/(sin (π−θ)))=((mg)/(sin (θ−α)))=(N/(sin α)) sin (θ−α)=(m/M) sin θ=η sin θ ⇒θ−α=sin^(−1) (η sin θ) ⇒α=θ−sin^(−1) (η sin θ) N=((Mg sin α)/(sin θ)) a=((h sin α)/(sin ((π/2)+θ−α)))=((h sin α)/(cos (θ−α)))=((h sin α)/( (√(1−η^2 sin^2 θ)))) ⇒((MgL cos θ)/2)=((Mg sin α)/(sin θ))×((h sin α)/( (√(1−η^2 sin^2 θ)))) ⇒((cos θ)/2)×(L/h)=((sin^2 α)/(sin θ (√(1−η^2 sin^2 θ)))) ⇒((λ sin θ cos θ (√(1−η^2 sin^2 θ)))/2)=sin^2 α ⇒λ sin 2θ (√(1−η^2 sin^2 θ))=2(1−cos 2α) ⇒λ sin 2θ (√(1−η^2 sin^2 θ))=2[1−cos 2{θ−sin^(−1) (η sin θ)}] examples: λ=(L/h)=2, η=(m/M)=0.2⇒θ=52.7639° λ=(L/h)=2, η=(m/M)=0⇒θ=45°](https://www.tinkutara.com/question/Q52835.png)
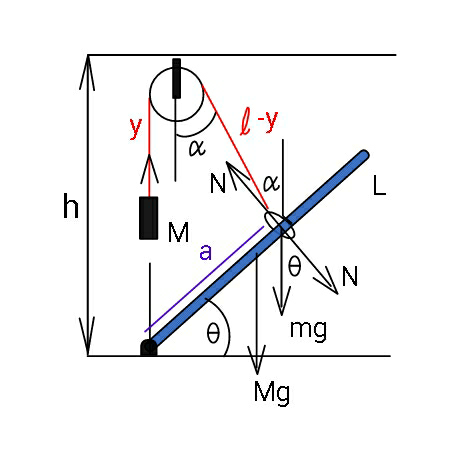
$${let}\:\eta=\frac{{m}}{{M}},\:\lambda=\frac{{L}}{{h}} \\ $$$$\alpha={angle}\:{between}\:{string}\:{and}\:{vertical} \\ $$$${a}={distance}\:{from}\:{ring}\:{to}\:{lower}\:{end}\:{of}\:{rod} \\ $$$${N}={contact}\:{force}\:{between}\:{ring}\:{and}\:{rod} \\ $$$$\frac{{MgL}\:\mathrm{cos}\:\theta}{\mathrm{2}}={Na} \\ $$$$\frac{{Mg}}{\mathrm{sin}\:\left(\pi−\theta\right)}=\frac{{mg}}{\mathrm{sin}\:\left(\theta−\alpha\right)}=\frac{{N}}{\mathrm{sin}\:\alpha} \\ $$$$\mathrm{sin}\:\left(\theta−\alpha\right)=\frac{{m}}{{M}}\:\mathrm{sin}\:\theta=\eta\:\mathrm{sin}\:\theta \\ $$$$\Rightarrow\theta−\alpha=\mathrm{sin}^{−\mathrm{1}} \left(\eta\:\mathrm{sin}\:\theta\right) \\ $$$$\Rightarrow\alpha=\theta−\mathrm{sin}^{−\mathrm{1}} \left(\eta\:\mathrm{sin}\:\theta\right) \\ $$$${N}=\frac{{Mg}\:\mathrm{sin}\:\alpha}{\mathrm{sin}\:\theta} \\ $$$${a}=\frac{{h}\:\mathrm{sin}\:\alpha}{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}+\theta−\alpha\right)}=\frac{{h}\:\mathrm{sin}\:\alpha}{\mathrm{cos}\:\left(\theta−\alpha\right)}=\frac{{h}\:\mathrm{sin}\:\alpha}{\:\sqrt{\mathrm{1}−\eta^{\mathrm{2}} \:\mathrm{sin}^{\mathrm{2}} \:\theta}} \\ $$$$\Rightarrow\frac{{MgL}\:\mathrm{cos}\:\theta}{\mathrm{2}}=\frac{{Mg}\:\mathrm{sin}\:\alpha}{\mathrm{sin}\:\theta}×\frac{{h}\:\mathrm{sin}\:\alpha}{\:\sqrt{\mathrm{1}−\eta^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta}} \\ $$$$\Rightarrow\frac{\mathrm{cos}\:\theta}{\mathrm{2}}×\frac{{L}}{{h}}=\frac{\mathrm{sin}^{\mathrm{2}} \:\alpha}{\mathrm{sin}\:\theta\:\sqrt{\mathrm{1}−\eta^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta}} \\ $$$$\Rightarrow\frac{\lambda\:\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta\:\sqrt{\mathrm{1}−\eta^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta}}{\mathrm{2}}=\mathrm{sin}^{\mathrm{2}} \:\alpha \\ $$$$\Rightarrow\lambda\:\mathrm{sin}\:\mathrm{2}\theta\:\sqrt{\mathrm{1}−\eta^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta}=\mathrm{2}\left(\mathrm{1}−\mathrm{cos}\:\mathrm{2}\alpha\right) \\ $$$$\Rightarrow\lambda\:\mathrm{sin}\:\mathrm{2}\theta\:\sqrt{\mathrm{1}−\eta^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta}=\mathrm{2}\left[\mathrm{1}−\mathrm{cos}\:\:\mathrm{2}\left\{\theta−\mathrm{sin}^{−\mathrm{1}} \left(\eta\:\mathrm{sin}\:\theta\right)\right\}\right] \\ $$$$ \\ $$$${examples}: \\ $$$$\lambda=\frac{{L}}{{h}}=\mathrm{2},\:\eta=\frac{{m}}{{M}}=\mathrm{0}.\mathrm{2}\Rightarrow\theta=\mathrm{52}.\mathrm{7639}° \\ $$$$\lambda=\frac{{L}}{{h}}=\mathrm{2},\:\eta=\frac{{m}}{{M}}=\mathrm{0}\Rightarrow\theta=\mathrm{45}° \\ $$
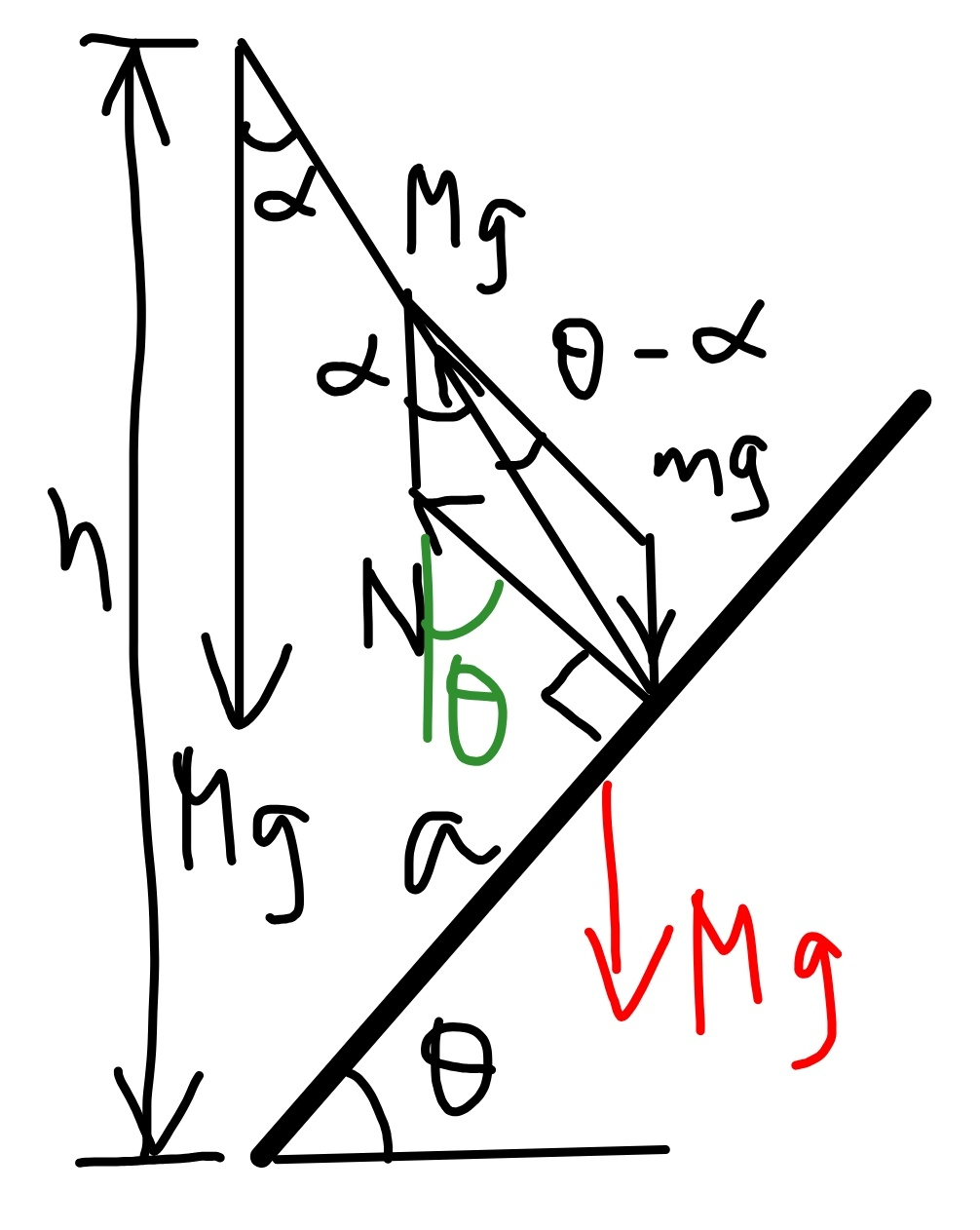
Commented by mr W last updated on 13/Jan/19
Commented by ajfour last updated on 14/Jan/19
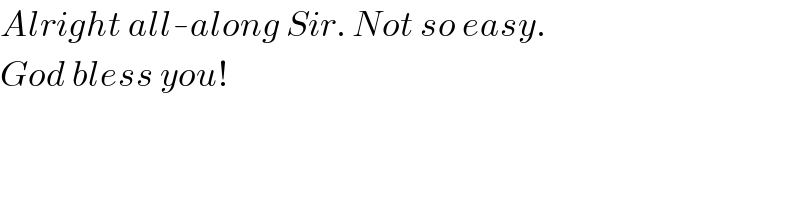
$${Alright}\:{all}-{along}\:{Sir}.\:{Not}\:{so}\:{easy}. \\ $$$${God}\:{bless}\:{you}! \\ $$
