Menu Close

Question-52841

Tinku Tara 0 Comments
Pin




Question Number 52841 by Tawa1 last updated on 13/Jan/19
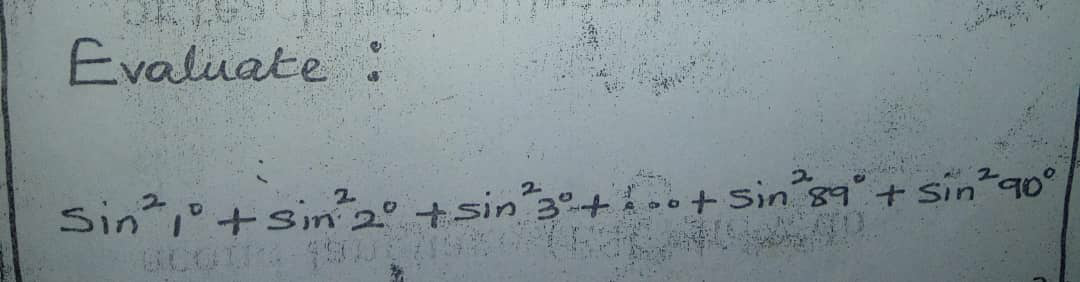
Commented by maxmathsup by imad last updated on 14/Jan/19
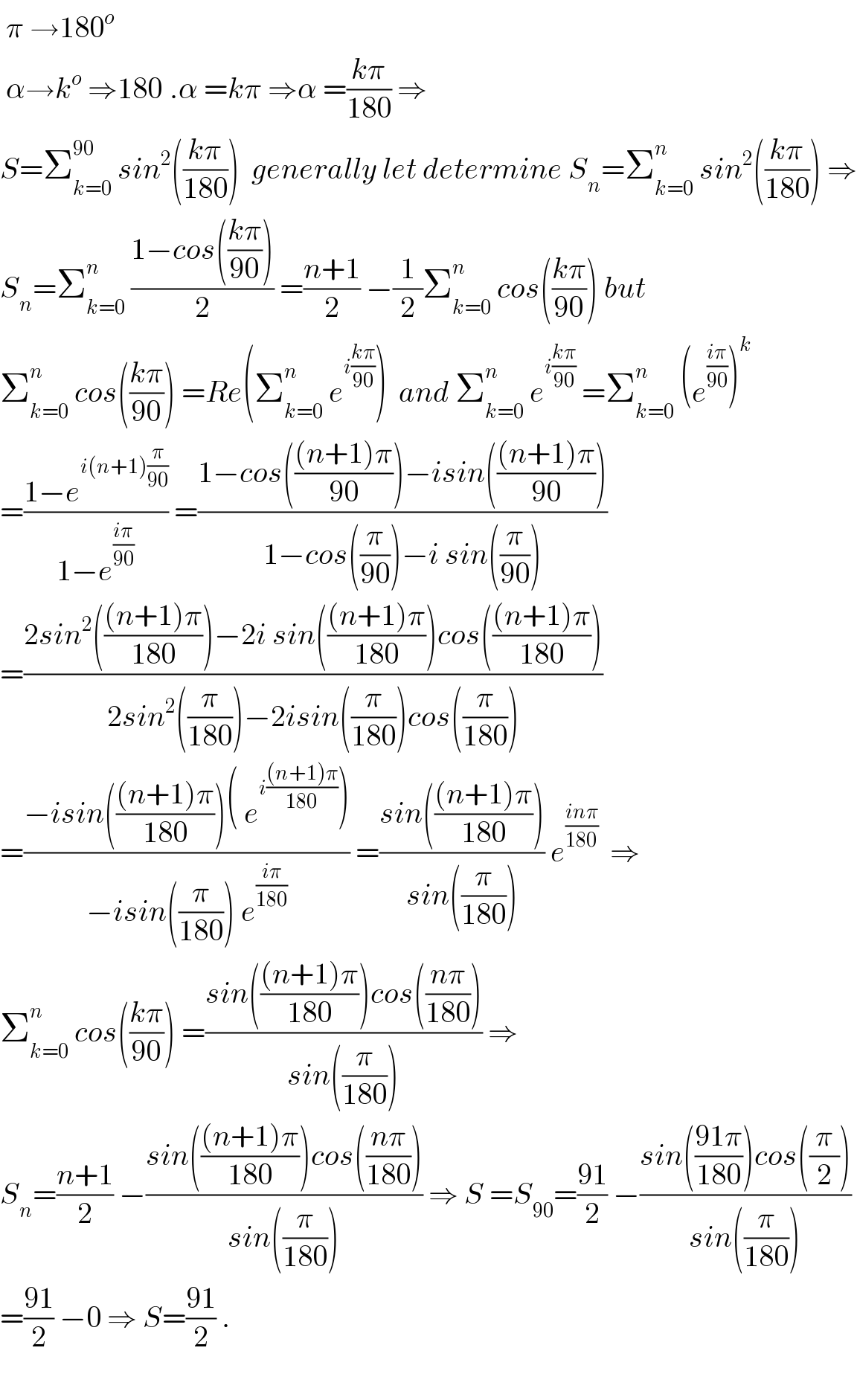
π →180^o α→k^o ⇒180^ .α =kπ ⇒α =((kπ)/(180)) ⇒ S=Σ_(k=0) ^(90) sin^2 (((kπ)/(180))) generally let determine S_n =Σ_(k=0) ^n sin^2 (((kπ)/(180))) ⇒ S_n =Σ_(k=0) ^n ((1−cos(((kπ)/(90))))/2) =((n+1)/2) −(1/2)Σ_(k=0) ^n cos(((kπ)/(90))) but Σ_(k=0) ^n cos(((kπ)/(90))) =Re(Σ_(k=0) ^n e^(i((kπ)/(90))) ) and Σ_(k=0) ^n e^(i((kπ)/(90))) =Σ_(k=0) ^n (e^((iπ)/(90)) )^k =((1−e^(i(n+1)(π/(90))) )/(1−e^((iπ)/(90)) )) =((1−cos((((n+1)π)/(90)))−isin((((n+1)π)/(90))))/(1−cos((π/(90)))−i sin((π/(90))))) =((2sin^2 ((((n+1)π)/(180)))−2i sin((((n+1)π)/(180)))cos((((n+1)π)/(180))))/(2sin^2 ((π/(180)))−2isin((π/(180)))cos((π/(180))))) =((−isin((((n+1)π)/(180)))( e^(i(((n+1)π)/(180))) ))/(−isin((π/(180))) e^((iπ)/(180)) )) =((sin((((n+1)π)/(180))))/(sin((π/(180))))) e^((inπ)/(180)) ⇒ Σ_(k=0) ^n cos(((kπ)/(90))) =((sin((((n+1)π)/(180)))cos(((nπ)/(180))))/(sin((π/(180))))) ⇒ S_n =((n+1)/2) −((sin((((n+1)π)/(180)))cos(((nπ)/(180))))/(sin((π/(180))))) ⇒ S =S_(90) =((91)/2) −((sin(((91π)/(180)))cos((π/2)))/(sin((π/(180))))) =((91)/2) −0 ⇒ S=((91)/2) .
$$\:\pi\:\rightarrow\mathrm{180}^{{o}} \\ $$$$\:\alpha\rightarrow{k}^{{o}} \:\Rightarrow\mathrm{180}^{} .\alpha\:={k}\pi\:\Rightarrow\alpha\:=\frac{{k}\pi}{\mathrm{180}}\:\Rightarrow \\ $$$${S}=\sum_{{k}=\mathrm{0}} ^{\mathrm{90}} \:{sin}^{\mathrm{2}} \left(\frac{{k}\pi}{\mathrm{180}}\right)\:\:{generally}\:{let}\:{determine}\:{S}_{{n}} =\sum_{{k}=\mathrm{0}} ^{{n}} \:{sin}^{\mathrm{2}} \left(\frac{{k}\pi}{\mathrm{180}}\right)\:\Rightarrow \\ $$$${S}_{{n}} =\sum_{{k}=\mathrm{0}} ^{{n}} \:\frac{\mathrm{1}−{cos}\left(\frac{{k}\pi}{\mathrm{90}}\right)}{\mathrm{2}}\:=\frac{{n}+\mathrm{1}}{\mathrm{2}}\:−\frac{\mathrm{1}}{\mathrm{2}}\sum_{{k}=\mathrm{0}} ^{{n}} \:{cos}\left(\frac{{k}\pi}{\mathrm{90}}\right)\:{but} \\ $$$$\sum_{{k}=\mathrm{0}} ^{{n}} \:{cos}\left(\frac{{k}\pi}{\mathrm{90}}\right)\:={Re}\left(\sum_{{k}=\mathrm{0}} ^{{n}} \:{e}^{{i}\frac{{k}\pi}{\mathrm{90}}} \right)\:\:{and}\:\sum_{{k}=\mathrm{0}} ^{{n}} \:{e}^{{i}\frac{{k}\pi}{\mathrm{90}}} \:=\sum_{{k}=\mathrm{0}} ^{{n}} \:\left({e}^{\frac{{i}\pi}{\mathrm{90}}} \right)^{{k}} \\ $$$$=\frac{\mathrm{1}−{e}^{{i}\left({n}+\mathrm{1}\right)\frac{\pi}{\mathrm{90}}} }{\mathrm{1}−{e}^{\frac{{i}\pi}{\mathrm{90}}} }\:=\frac{\mathrm{1}−{cos}\left(\frac{\left({n}+\mathrm{1}\right)\pi}{\mathrm{90}}\right)−{isin}\left(\frac{\left({n}+\mathrm{1}\right)\pi}{\mathrm{90}}\right)}{\mathrm{1}−{cos}\left(\frac{\pi}{\mathrm{90}}\right)−{i}\:{sin}\left(\frac{\pi}{\mathrm{90}}\right)}\: \\ $$$$=\frac{\mathrm{2}{sin}^{\mathrm{2}} \left(\frac{\left({n}+\mathrm{1}\right)\pi}{\mathrm{180}}\right)−\mathrm{2}{i}\:{sin}\left(\frac{\left({n}+\mathrm{1}\right)\pi}{\mathrm{180}}\right){cos}\left(\frac{\left({n}+\mathrm{1}\right)\pi}{\mathrm{180}}\right)}{\mathrm{2}{sin}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{180}}\right)−\mathrm{2}{isin}\left(\frac{\pi}{\mathrm{180}}\right){cos}\left(\frac{\pi}{\mathrm{180}}\right)} \\ $$$$=\frac{−{isin}\left(\frac{\left({n}+\mathrm{1}\right)\pi}{\mathrm{180}}\right)\left(\:{e}^{{i}\frac{\left({n}+\mathrm{1}\right)\pi}{\mathrm{180}}} \right)}{−{isin}\left(\frac{\pi}{\mathrm{180}}\right)\:{e}^{\frac{{i}\pi}{\mathrm{180}}} }\:=\frac{{sin}\left(\frac{\left({n}+\mathrm{1}\right)\pi}{\mathrm{180}}\right)}{{sin}\left(\frac{\pi}{\mathrm{180}}\right)}\:{e}^{\frac{{in}\pi}{\mathrm{180}}} \:\:\Rightarrow \\ $$$$\sum_{{k}=\mathrm{0}} ^{{n}} \:{cos}\left(\frac{{k}\pi}{\mathrm{90}}\right)\:=\frac{{sin}\left(\frac{\left({n}+\mathrm{1}\right)\pi}{\mathrm{180}}\right){cos}\left(\frac{{n}\pi}{\mathrm{180}}\right)}{{sin}\left(\frac{\pi}{\mathrm{180}}\right)}\:\Rightarrow \\ $$$${S}_{{n}} =\frac{{n}+\mathrm{1}}{\mathrm{2}}\:−\frac{{sin}\left(\frac{\left({n}+\mathrm{1}\right)\pi}{\mathrm{180}}\right){cos}\left(\frac{{n}\pi}{\mathrm{180}}\right)}{{sin}\left(\frac{\pi}{\mathrm{180}}\right)}\:\Rightarrow\:{S}\:={S}_{\mathrm{90}} =\frac{\mathrm{91}}{\mathrm{2}}\:−\frac{{sin}\left(\frac{\mathrm{91}\pi}{\mathrm{180}}\right){cos}\left(\frac{\pi}{\mathrm{2}}\right)}{{sin}\left(\frac{\pi}{\mathrm{180}}\right)} \\ $$$$=\frac{\mathrm{91}}{\mathrm{2}}\:−\mathrm{0}\:\Rightarrow\:{S}=\frac{\mathrm{91}}{\mathrm{2}}\:. \\ $$$$ \\ $$
Commented by Tawa1 last updated on 16/Jan/19
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}\: \\ $$
Commented by Tawa1 last updated on 17/Jan/19
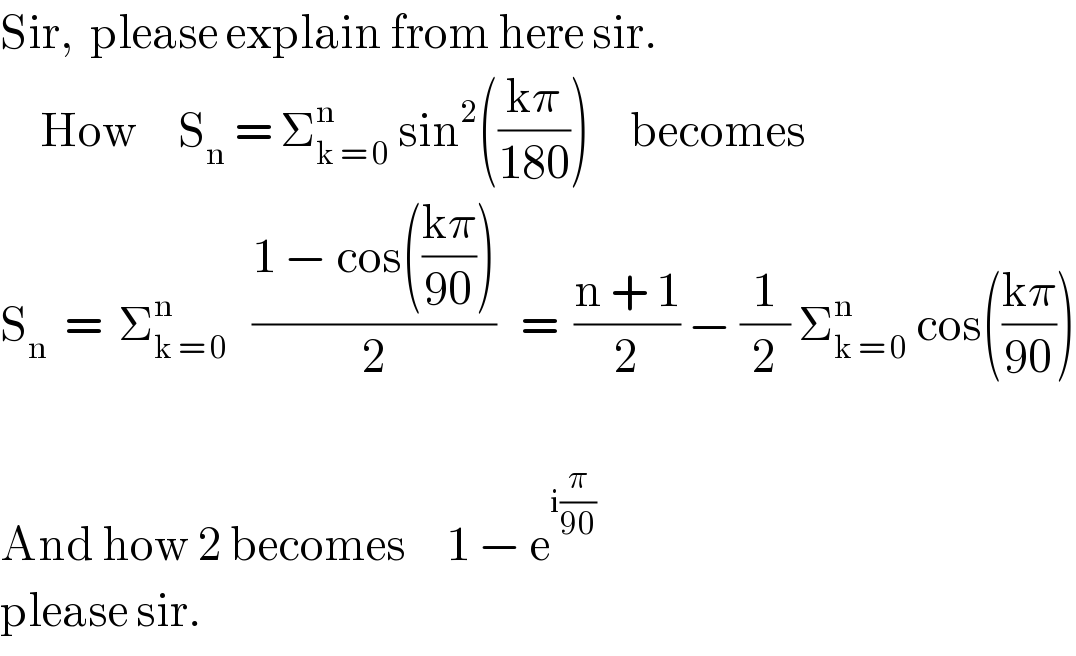
Sir, please explain from here sir. How S_n = Σ_(k = 0) ^n sin^2 (((kπ)/(180))) becomes S_n = Σ_(k = 0) ^n ((1 − cos(((kπ)/(90))))/2) = ((n + 1)/2) − (1/2) Σ_(k = 0) ^(n ) cos(((kπ)/(90))) And how 2 becomes 1 − e^(i(π/(90))) please sir.
$$\mathrm{Sir},\:\:\mathrm{please}\:\mathrm{explain}\:\mathrm{from}\:\mathrm{here}\:\mathrm{sir}. \\ $$$$\:\:\:\:\:\mathrm{How}\:\:\:\:\:\mathrm{S}_{\mathrm{n}} \:=\:\sum_{\mathrm{k}\:=\:\mathrm{0}} ^{\mathrm{n}} \:\mathrm{sin}^{\mathrm{2}} \left(\frac{\mathrm{k}\pi}{\mathrm{180}}\right)\:\:\:\:\:\mathrm{becomes}\:\:\: \\ $$$$\mathrm{S}_{\mathrm{n}} \:\:=\:\:\sum_{\mathrm{k}\:=\:\mathrm{0}} ^{\mathrm{n}} \:\:\:\frac{\mathrm{1}\:−\:\mathrm{cos}\left(\frac{\mathrm{k}\pi}{\mathrm{90}}\right)}{\mathrm{2}}\:\:\:=\:\:\frac{\mathrm{n}\:+\:\mathrm{1}}{\mathrm{2}}\:−\:\frac{\mathrm{1}}{\mathrm{2}}\:\sum_{\mathrm{k}\:=\:\mathrm{0}} ^{\mathrm{n}\:} \:\mathrm{cos}\left(\frac{\mathrm{k}\pi}{\mathrm{90}}\right) \\ $$$$ \\ $$$$\mathrm{And}\:\mathrm{how}\:\mathrm{2}\:\mathrm{becomes}\:\:\:\:\:\mathrm{1}\:−\:\mathrm{e}^{\mathrm{i}\frac{\pi}{\mathrm{90}}} \\ $$$$\mathrm{please}\:\mathrm{sir}. \\ $$
Commented by maxmathsup by imad last updated on 19/Jan/19
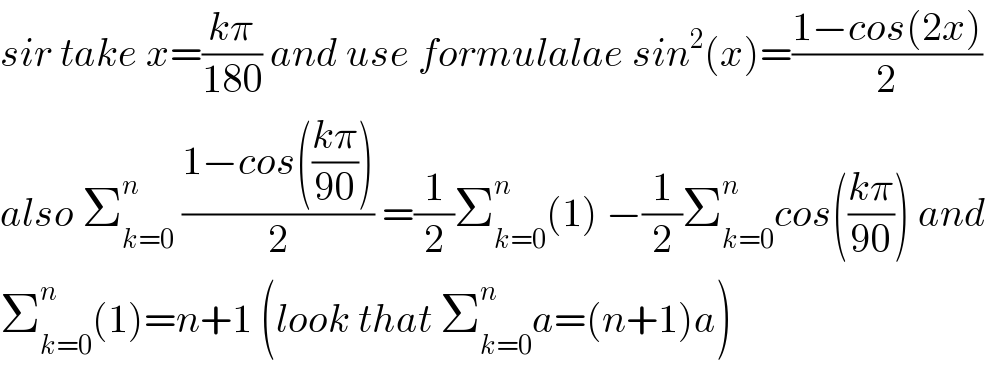
sir take x=((kπ)/(180)) and use formulalae sin^2 (x)=((1−cos(2x))/2) also Σ_(k=0) ^n ((1−cos(((kπ)/(90))))/2) =(1/2)Σ_(k=0) ^n (1) −(1/2)Σ_(k=0) ^n cos(((kπ)/(90))) and Σ_(k=0) ^n (1)=n+1 (look that Σ_(k=0) ^n a=(n+1)a)
$${sir}\:{take}\:{x}=\frac{{k}\pi}{\mathrm{180}}\:{and}\:{use}\:{formulalae}\:{sin}^{\mathrm{2}} \left({x}\right)=\frac{\mathrm{1}−{cos}\left(\mathrm{2}{x}\right)}{\mathrm{2}} \\ $$$${also}\:\sum_{{k}=\mathrm{0}} ^{{n}} \:\frac{\mathrm{1}−{cos}\left(\frac{{k}\pi}{\mathrm{90}}\right)}{\mathrm{2}}\:=\frac{\mathrm{1}}{\mathrm{2}}\sum_{{k}=\mathrm{0}} ^{{n}} \left(\mathrm{1}\right)\:−\frac{\mathrm{1}}{\mathrm{2}}\sum_{{k}=\mathrm{0}} ^{{n}} {cos}\left(\frac{{k}\pi}{\mathrm{90}}\right)\:{and}\: \\ $$$$\sum_{{k}=\mathrm{0}} ^{{n}} \left(\mathrm{1}\right)={n}+\mathrm{1}\:\left({look}\:{that}\:\sum_{{k}=\mathrm{0}} ^{{n}} {a}=\left({n}+\mathrm{1}\right){a}\right) \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 14/Jan/19
1+89=90 so sin^2 1+sin^2 89 =sin^2 1+sin^2 (90−1) =sin^2 1+cos^2 1 =1 similarly.. 2+88=90 ... ... 45+45=90 s=(sin^2 1+sin^2 2+sin^2 3+...+sin^2 89)+sin^2 90 s=(sin^2 89+sin^2 88+sin^2 87+..+sin^2 1)+sin^2 90 2s=[(sin^2 1+sin^2 89)+(sin^2 2+sin^2 88)+..+(sin^2 89+sin^2 1)]+(1+1) 2s=[1+1+1...89times]+2 s=((91)/2)=45.5
$$\mathrm{1}+\mathrm{89}=\mathrm{90}\:\:{so}\:\:{sin}^{\mathrm{2}} \mathrm{1}+{sin}^{\mathrm{2}} \mathrm{89} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:={sin}^{\mathrm{2}} \mathrm{1}+{sin}^{\mathrm{2}} \left(\mathrm{90}−\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:={sin}^{\mathrm{2}} \mathrm{1}+{cos}^{\mathrm{2}} \mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{1} \\ $$$${similarly}.. \\ $$$$\mathrm{2}+\mathrm{88}=\mathrm{90} \\ $$$$… \\ $$$$… \\ $$$$\mathrm{45}+\mathrm{45}=\mathrm{90} \\ $$$$ \\ $$$${s}=\left({sin}^{\mathrm{2}} \mathrm{1}+{sin}^{\mathrm{2}} \mathrm{2}+{sin}^{\mathrm{2}} \mathrm{3}+…+{sin}^{\mathrm{2}} \mathrm{89}\right)+{sin}^{\mathrm{2}} \mathrm{90} \\ $$$${s}=\left({sin}^{\mathrm{2}} \mathrm{89}+{sin}^{\mathrm{2}} \mathrm{88}+{sin}^{\mathrm{2}} \mathrm{87}+..+{sin}^{\mathrm{2}} \mathrm{1}\right)+{sin}^{\mathrm{2}} \mathrm{90} \\ $$$$\:\mathrm{2}{s}=\left[\left({sin}^{\mathrm{2}} \mathrm{1}+{sin}^{\mathrm{2}} \mathrm{89}\right)+\left({sin}^{\mathrm{2}} \mathrm{2}+{sin}^{\mathrm{2}} \mathrm{88}\right)+..+\left({sin}^{\mathrm{2}} \mathrm{89}+{sin}^{\mathrm{2}} \mathrm{1}\right)\right]+\left(\mathrm{1}+\mathrm{1}\right) \\ $$$$\mathrm{2}{s}=\left[\mathrm{1}+\mathrm{1}+\mathrm{1}…\mathrm{89}{times}\right]+\mathrm{2} \\ $$$${s}=\frac{\mathrm{91}}{\mathrm{2}}=\mathrm{45}.\mathrm{5} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 14/Jan/19
thank you..God bless all...
$${thank}\:{you}..{God}\:{bless}\:{all}… \\ $$
Commented by Tawa1 last updated on 14/Jan/19
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *