Question Number 52859 by tanmay.chaudhury50@gmail.com last updated on 14/Jan/19
Commented by tanmay.chaudhury50@gmail.com last updated on 14/Jan/19
Commented by tanmay.chaudhury50@gmail.com last updated on 14/Jan/19
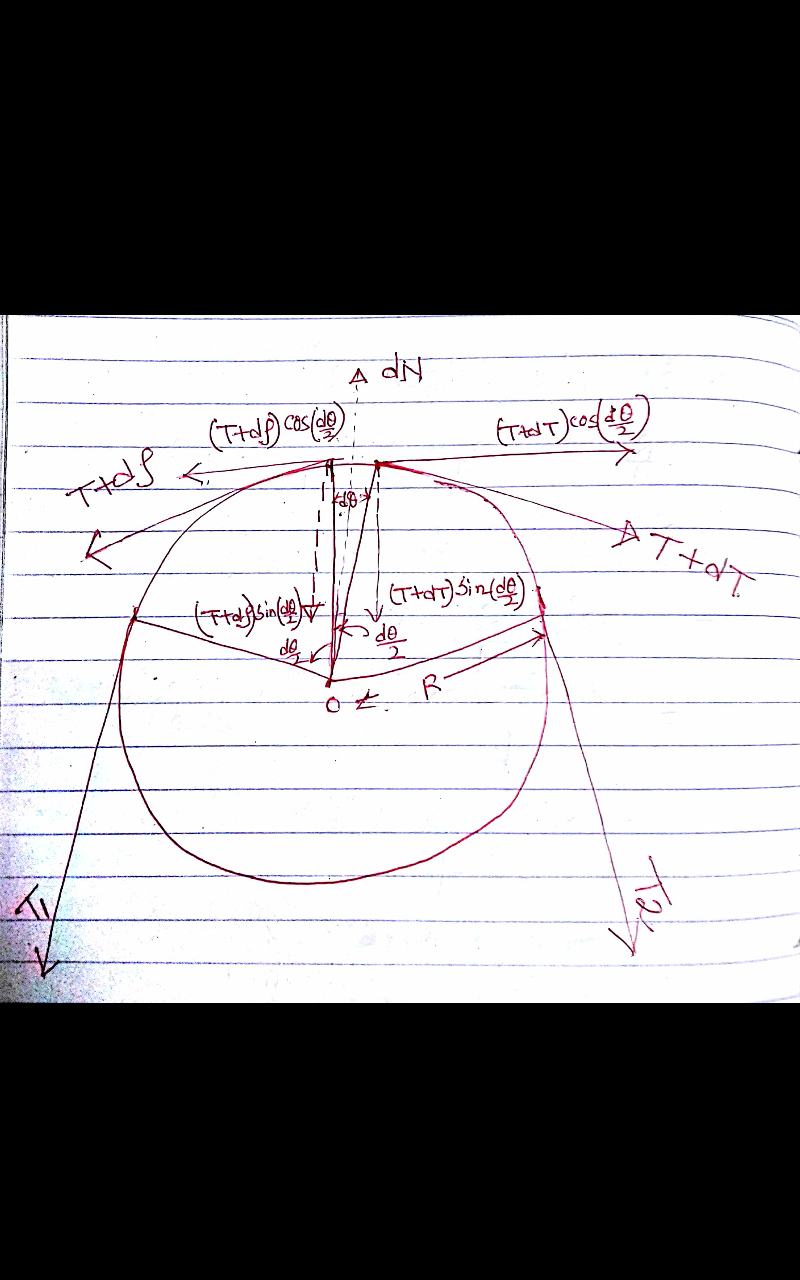
![Here T_2 >T_1 so the string have a tendency to slide clockwise,to balance friction acts to play As the difference of T_2 and T_1 increases friction also increases till it reach limiting friction,then string starts slupping. considering small element of string in contact with pully.T+dT of right side is balanced by T+df of left side. df=frictional force so T+dT=T+df dT=df from digram... (T+dT)sin((dθ/2))+(T+df)sin((dθ/2))=dN(normal reaction) 2(T+dT)sin((dθ/2))=dN [since df=dT] 2(T+dT)((dθ/2))=dN Tdθ+dTdθ=dN [dTdθ=negligible] Tdθ=dN df=μdN [friction=coefficient of staticfriction×normal reaction] df=dT=μdN so dN=(dT/μ) Tdθ=(dT/μ) ∫_T_1 ^T_2 (dT/T)=μ∫_0 ^θ dθ ln((T_2 /T_1 ))=μθ (T_2 /T_1 )=e^(μθ) T_2 =T_1 e^(μθ) i have seen this in some book hence shared](https://www.tinkutara.com/question/Q52877.png)
$${Here}\:{T}_{\mathrm{2}} >{T}_{\mathrm{1}} \:{so}\:{the}\:{string}\:{have}\:{a}\:{tendency}\:{to} \\ $$$${slide}\:{clockwise},{to}\:{balance}\:{friction}\:{acts}\:{to}\:{play} \\ $$$${As}\:{the}\:{difference}\:{of}\:{T}_{\mathrm{2}} \:{and}\:{T}_{\mathrm{1}} \:{increases} \\ $$$${friction}\:{also}\:{increases}\:{till}\:{it}\:{reach}\:{limiting} \\ $$$${friction},{then}\:{string}\:{starts}\:{slupping}. \\ $$$${considering}\:{small}\:{element}\:{of}\:{string}\:{in}\:{contact} \\ $$$${with}\:{pully}.{T}+{dT}\:{of}\:{right}\:{side}\:{is}\:{balanced} \\ $$$${by}\:{T}+{df}\:{of}\:{left}\:{side}.\:{df}={frictional}\:{force} \\ $$$${so}\:{T}+{dT}={T}+{df}\:\:\:\:\:{dT}={df} \\ $$$${from}\:{digram}… \\ $$$$\left({T}+{dT}\right){sin}\left(\frac{{d}\theta}{\mathrm{2}}\right)+\left({T}+{df}\right){sin}\left(\frac{{d}\theta}{\mathrm{2}}\right)={dN}\left({normal}\:{reaction}\right) \\ $$$$\mathrm{2}\left({T}+{dT}\right){sin}\left(\frac{{d}\theta}{\mathrm{2}}\right)={dN}\:\:\left[{since}\:{df}={dT}\right] \\ $$$$\mathrm{2}\left({T}+{dT}\right)\left(\frac{{d}\theta}{\mathrm{2}}\right)={dN} \\ $$$${Td}\theta+{dTd}\theta={dN}\:\:\left[{dTd}\theta={negligible}\right] \\ $$$${Td}\theta={dN} \\ $$$${df}=\mu{dN}\:\left[{friction}={coefficient}\:{of}\:{staticfriction}×{normal}\:{reaction}\right] \\ $$$${df}={dT}=\mu{dN}\:\:\:\:{so}\:\:{dN}=\frac{{dT}}{\mu} \\ $$$${Td}\theta=\frac{{dT}}{\mu} \\ $$$$\int_{{T}_{\mathrm{1}} } ^{{T}_{\mathrm{2}} } \frac{{dT}}{{T}}=\mu\int_{\mathrm{0}} ^{\theta} {d}\theta \\ $$$${ln}\left(\frac{{T}_{\mathrm{2}} }{{T}_{\mathrm{1}} }\right)=\mu\theta\:\: \\ $$$$\frac{{T}_{\mathrm{2}} }{{T}_{\mathrm{1}} }={e}^{\mu\theta} \:\:\:\:\:\:\:\:\:{T}_{\mathrm{2}} ={T}_{\mathrm{1}} {e}^{\mu\theta} \\ $$$${i}\:{have}\:{seen}\:{this}\:{in}\:{some}\:{book}\:{hence}\:{shared} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 14/Jan/19
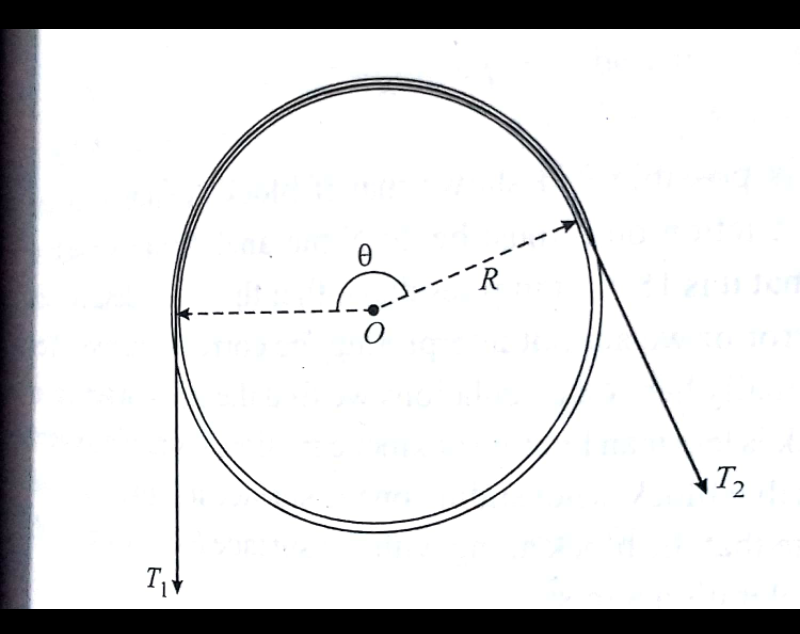
![A string is passing over the surface of a pully which is free to rotate about an axis passing through O,the angle of contact of the string ln the pully is θ,the static friction coefficient between pully and string is μ. prove T_2 =T_1 e^(μθ) [T_2 >T_1 ]](https://www.tinkutara.com/question/Q52860.png)
$${A}\:{string}\:{is}\:{passing}\:{over}\:{the}\:{surface}\:{of}\:{a}\:{pully} \\ $$$${which}\:{is}\:{free}\:{to}\:{rotate}\:{about}\:{an}\:{axis}\:{passing} \\ $$$${through}\:{O},{the}\:{angle}\:{of}\:{contact}\:{of}\:{the}\:{string} \\ $$$${ln}\:{the}\:{pully}\:{is}\:\theta,{the}\:{static}\:{friction}\:{coefficient} \\ $$$${between}\:{pully}\:{and}\:{string}\:{is}\:\mu. \\ $$$${prove}\:{T}_{\mathrm{2}} ={T}_{\mathrm{1}} {e}^{\mu\theta} \:\:\:\:\left[{T}_{\mathrm{2}} >{T}_{\mathrm{1}} \right] \\ $$
