Menu Close

Question-52867

Tinku Tara 0 Comments
Pin




Question Number 52867 by hassentimol last updated on 14/Jan/19
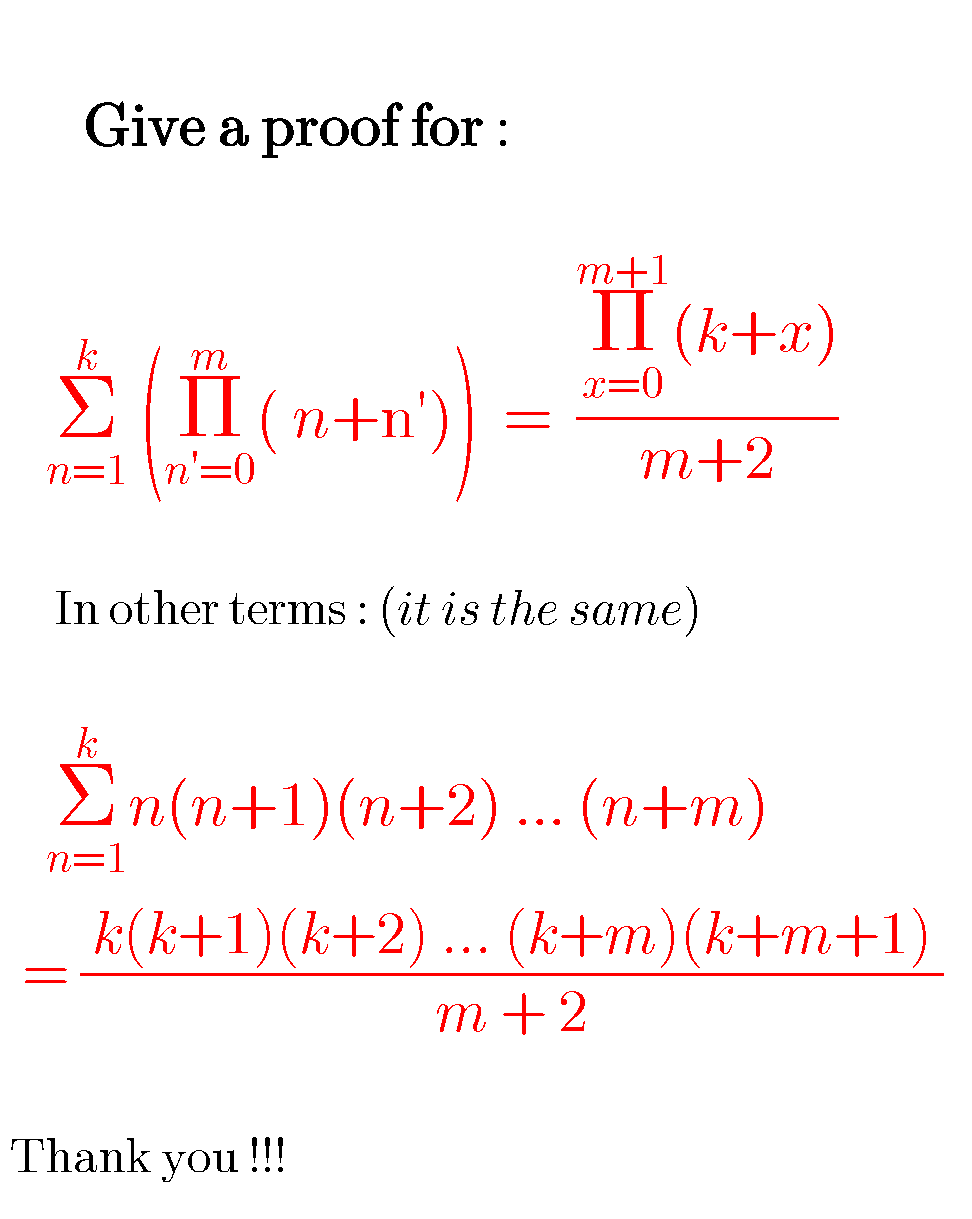
Answered by iv@0uja last updated on 19/Jan/19
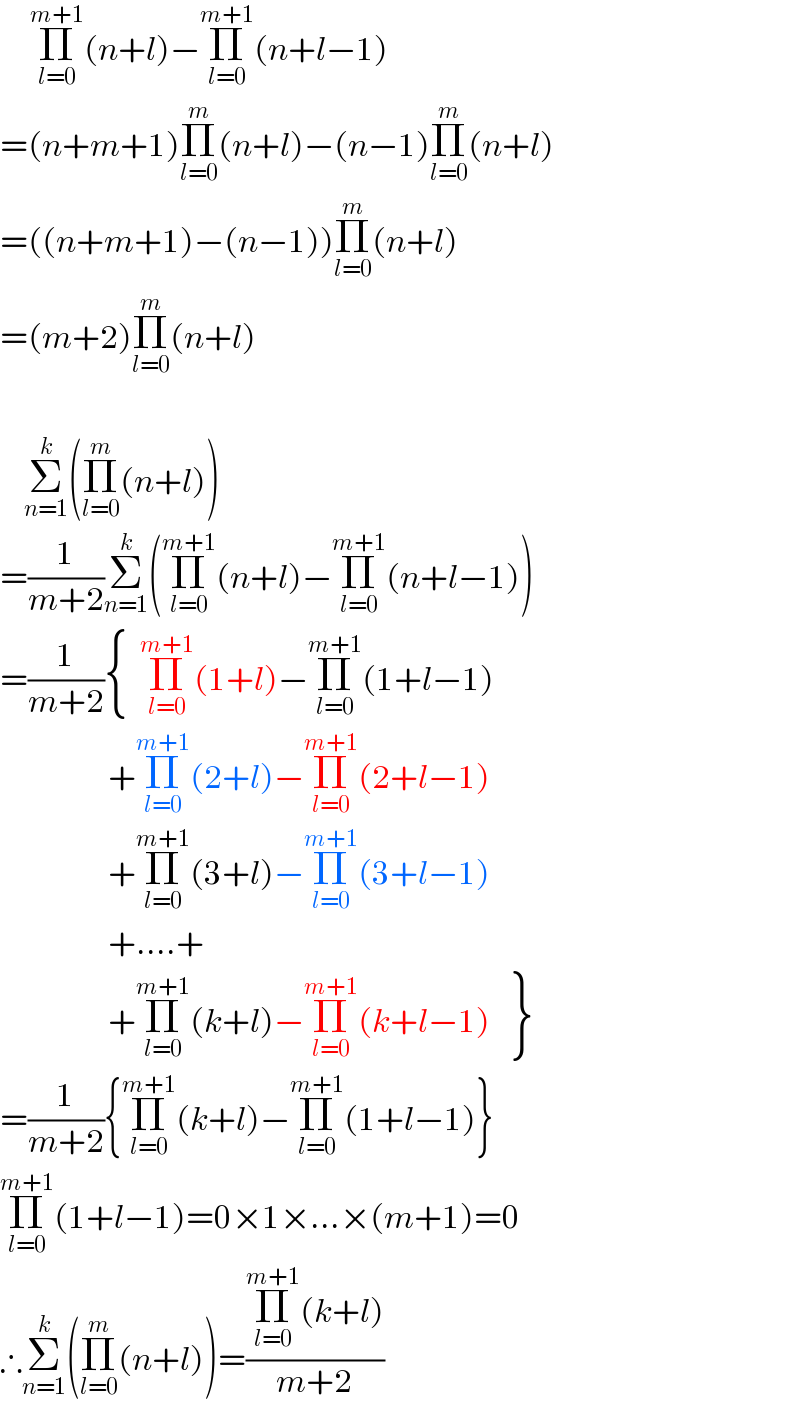
Π_(l=0) ^(m+1) (n+l)−Π_(l=0) ^(m+1) (n+l−1) =(n+m+1)Π_(l=0) ^m (n+l)−(n−1)Π_(l=0) ^m (n+l) =((n+m+1)−(n−1))Π_(l=0) ^m (n+l) =(m+2)Π_(l=0) ^m (n+l) Σ_(n=1) ^k (Π_(l=0) ^m (n+l)) =(1/(m+2))Σ_(n=1) ^k (Π_(l=0) ^(m+1) (n+l)−Π_(l=0) ^(m+1) (n+l−1)) =(1/(m+2)) { (),() :}Π_(l=0) ^(m+1) (1+l)−Π_(l=0) ^(m+1) (1+l−1) +Π_(l=0) ^(m+1) (2+l)−Π_(l=0) ^(m+1) (2+l−1) +Π_(l=0) ^(m+1) (3+l)−Π_(l=0) ^(m+1) (3+l−1) +....+ +Π_(l=0) ^(m+1) (k+l)−Π_(l=0) ^(m+1) (k+l−1) {: (),() } =(1/(m+2)){Π_(l=0) ^(m+1) (k+l)−Π_(l=0) ^(m+1) (1+l−1)} Π_(l=0) ^(m+1) (1+l−1)=0×1×...×(m+1)=0 ∴Σ_(n=1) ^k (Π_(l=0) ^m (n+l))=((Π_(l=0) ^(m+1) (k+l))/(m+2))
$$\:\:\:\:\:\underset{{l}=\mathrm{0}} {\overset{{m}+\mathrm{1}} {\prod}}\left({n}+{l}\right)−\underset{{l}=\mathrm{0}} {\overset{{m}+\mathrm{1}} {\prod}}\left({n}+{l}−\mathrm{1}\right) \\ $$$$=\left({n}+{m}+\mathrm{1}\right)\underset{{l}=\mathrm{0}} {\overset{{m}} {\prod}}\left({n}+{l}\right)−\left({n}−\mathrm{1}\right)\underset{{l}=\mathrm{0}} {\overset{{m}} {\prod}}\left({n}+{l}\right) \\ $$$$=\left(\left({n}+{m}+\mathrm{1}\right)−\left({n}−\mathrm{1}\right)\right)\underset{{l}=\mathrm{0}} {\overset{{m}} {\prod}}\left({n}+{l}\right) \\ $$$$=\left({m}+\mathrm{2}\right)\underset{{l}=\mathrm{0}} {\overset{{m}} {\prod}}\left({n}+{l}\right) \\ $$$$ \\ $$$$\:\:\:\:\underset{{n}=\mathrm{1}} {\overset{{k}} {\sum}}\left(\underset{{l}=\mathrm{0}} {\overset{{m}} {\prod}}\left({n}+{l}\right)\right) \\ $$$$=\frac{\mathrm{1}}{{m}+\mathrm{2}}\underset{{n}=\mathrm{1}} {\overset{{k}} {\sum}}\left(\underset{{l}=\mathrm{0}} {\overset{{m}+\mathrm{1}} {\prod}}\left({n}+{l}\right)−\underset{{l}=\mathrm{0}} {\overset{{m}+\mathrm{1}} {\prod}}\left({n}+{l}−\mathrm{1}\right)\right) \\ $$$$=\frac{\mathrm{1}}{{m}+\mathrm{2}}\begin{cases}{}\\{}\end{cases}\underset{{l}=\mathrm{0}} {\overset{{m}+\mathrm{1}} {\prod}}\left(\mathrm{1}+{l}\right)−\underset{{l}=\mathrm{0}} {\overset{{m}+\mathrm{1}} {\prod}}\left(\mathrm{1}+{l}−\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\underset{{l}=\mathrm{0}} {\overset{{m}+\mathrm{1}} {\prod}}\left(\mathrm{2}+{l}\right)−\underset{{l}=\mathrm{0}} {\overset{{m}+\mathrm{1}} {\prod}}\left(\mathrm{2}+{l}−\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\underset{{l}=\mathrm{0}} {\overset{{m}+\mathrm{1}} {\prod}}\left(\mathrm{3}+{l}\right)−\underset{{l}=\mathrm{0}} {\overset{{m}+\mathrm{1}} {\prod}}\left(\mathrm{3}+{l}−\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+….+ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\underset{{l}=\mathrm{0}} {\overset{{m}+\mathrm{1}} {\prod}}\left({k}+{l}\right)−\underset{{l}=\mathrm{0}} {\overset{{m}+\mathrm{1}} {\prod}}\left({k}+{l}−\mathrm{1}\right)\left.\begin{matrix}{}\\{}\end{matrix}\right\} \\ $$$$=\frac{\mathrm{1}}{{m}+\mathrm{2}}\left\{\underset{{l}=\mathrm{0}} {\overset{{m}+\mathrm{1}} {\prod}}\left({k}+{l}\right)−\underset{{l}=\mathrm{0}} {\overset{{m}+\mathrm{1}} {\prod}}\left(\mathrm{1}+{l}−\mathrm{1}\right)\right\} \\ $$$$\underset{{l}=\mathrm{0}} {\overset{{m}+\mathrm{1}} {\prod}}\left(\mathrm{1}+{l}−\mathrm{1}\right)=\mathrm{0}×\mathrm{1}×…×\left({m}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\therefore\underset{{n}=\mathrm{1}} {\overset{{k}} {\sum}}\left(\underset{{l}=\mathrm{0}} {\overset{{m}} {\prod}}\left({n}+{l}\right)\right)=\frac{\underset{{l}=\mathrm{0}} {\overset{{m}+\mathrm{1}} {\prod}}\left({k}+{l}\right)}{{m}+\mathrm{2}} \\ $$
Commented by hassentimol last updated on 19/Jan/19
Oh... Thank you so much sir... I am so grateful... God Bless You !!!
$$\mathrm{Oh}…\:\mathrm{Thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much}\:\mathrm{sir}… \\ $$$$\mathrm{I}\:\mathrm{am}\:\mathrm{so}\:\mathrm{grateful}…\:\mathrm{God}\:\mathrm{Bless}\:\mathrm{You}\:!!! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *