Question Number 52938 by ajfour last updated on 15/Jan/19
Commented by ajfour last updated on 16/Jan/19

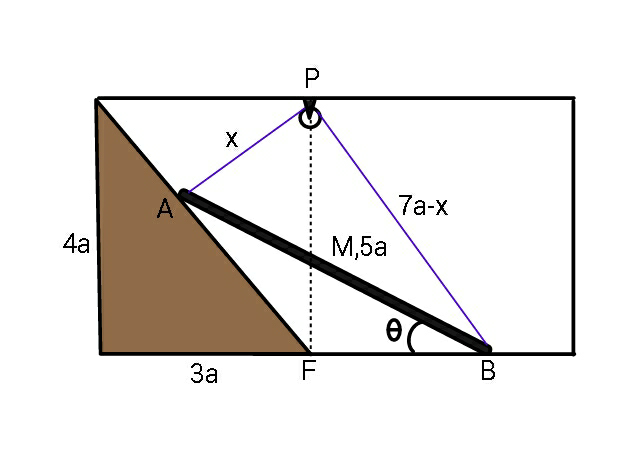
$${Find}\:\boldsymbol{{x}},\:{tension}\:\boldsymbol{{T}},\:{and}\:\boldsymbol{\theta}. \\ $$$${Assume}\:{friction}\:{is}\:{not}\:{present} \\ $$$${and}\:{rod}\:{is}\:{in}\:{equilibrium}.\:\:\:\:\: \\ $$
Commented by ajfour last updated on 16/Jan/19
Commented by ajfour last updated on 16/Jan/19

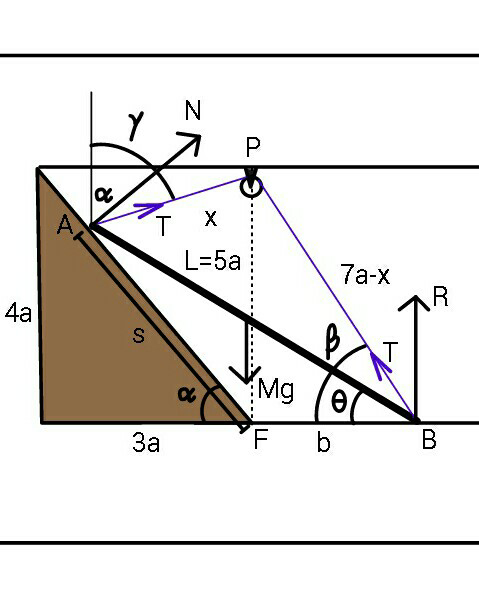
$$\mathrm{tan}\:\alpha\:=\:\frac{\mathrm{4}}{\mathrm{3}} \\ $$$${s}\mathrm{cos}\:\alpha+{b}={L}\mathrm{cos}\:\theta\:\: \\ $$$$\Rightarrow\:\:\frac{\mathrm{3}{s}}{\mathrm{5}}+{b}=\mathrm{5}{a}\mathrm{cos}\:\theta\:\:\:…\left({i}\right) \\ $$$$\:\:\:{x}\mathrm{sin}\:\gamma\:=\:{s}\mathrm{cos}\:\alpha \\ $$$$\Rightarrow\:\:\:\mathrm{5}{x}\mathrm{sin}\:\gamma=\mathrm{3}{s}\:\:\:\:\:\:\:\:\:…\left({ii}\right) \\ $$$$\:\:{s}\mathrm{sin}\:\alpha\:=\:{L}\mathrm{sin}\:\theta \\ $$$$\Rightarrow\:\:\:\:\:\mathrm{4}{s}\:=\mathrm{25}{a}\mathrm{sin}\:\theta\:\:\:\:\:…\left({iii}\right) \\ $$$$\:\:\:{x}\mathrm{cos}\:\gamma+{s}\mathrm{sin}\:\alpha\:=\:\mathrm{4}{a} \\ $$$$\Rightarrow\:\:\mathrm{5}{x}\mathrm{cos}\:\gamma+\mathrm{4}{s}=\mathrm{20}{a}\:\:\:\:…\left({iv}\right) \\ $$$$\:\:\:\:\:\:{b}\mathrm{tan}\:\beta\:=\:\mathrm{4}{a}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:….\left({v}\right) \\ $$$$\:\:\left(\mathrm{7}{a}−{x}\right)\mathrm{cos}\:\beta\:=\:{b}\:\:\:\:\:\:\:\:\:….\left({vi}\right) \\ $$$$\:\:{N}\mathrm{cos}\:\alpha+{T}\mathrm{cos}\:\gamma+{R}+{T}\mathrm{sin}\:\beta\:=\:{Mg} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:…..\left({vii}\right) \\ $$$$\:\:{N}\mathrm{sin}\:\alpha+{T}\mathrm{sin}\:\gamma\:=\:{T}\mathrm{cos}\:\beta\:\:\:\:…\left({viii}\right) \\ $$$$\:\:\Sigma{Torque}\:{about}\:{B}\:=\:\mathrm{0} \\ $$$$\Rightarrow\:{Mg}\mathrm{cos}\:\theta=\:{N}\mathrm{sin}\:\left(\theta+\frac{\pi}{\mathrm{2}}−\alpha\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+{T}\mathrm{sin}\:\left(\theta+\frac{\pi}{\mathrm{2}}−\gamma\right)\:\:\:\:\:…\left({ix}\right) \\ $$$${unknowns}\:{being}\: \\ $$$$\theta,{x}\:{b},{s},\beta,\gamma,{R},{N},{T}\:. \\ $$$${Solving}\:{all}\:{these}\:{eqs}.\:{in}\:{my}\:{little} \\ $$$${notebook}\:{i}\:{obtained}, \\ $$$$\:\:\:\:\frac{{x}}{{a}}=\sqrt{\frac{\mathrm{625}}{\mathrm{16}}\mathrm{sin}\:^{\mathrm{2}} \theta−\mathrm{40sin}\:\theta+\mathrm{16}} \\ $$$$\:\:\:\:{T}\:=\:\frac{\mathrm{4}{Mg}\mathrm{cos}\:\theta}{\mathrm{4cos}\:\left(\gamma−\theta\right)+\left(\mathrm{3cos}\:\theta+\mathrm{4sin}\:\theta\right)\left(\mathrm{cos}\:\beta−\mathrm{cos}\:\gamma\right)} \\ $$$$\:\:\:\mathrm{tan}\:\beta\:=\:\frac{\mathrm{16}}{\mathrm{5}\left(\mathrm{4cos}\:\theta−\mathrm{3sin}\:\theta\right)} \\ $$$$\:\:\:\mathrm{tan}\:\gamma\:=\:\frac{\mathrm{15sin}\:\theta}{\mathrm{16}−\mathrm{20sin}\:\theta} \\ $$$${while}\:\theta\:{is}\:{found}\:{from} \\ $$$$\frac{\mathrm{25}}{\mathrm{4}}\sqrt{\mathrm{sin}\:^{\mathrm{2}} \left(\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{4}}{\mathrm{5}}−\theta\right)+\frac{\mathrm{256}}{\mathrm{625}}}\: \\ $$$$\:\:\:+\sqrt{\frac{\mathrm{625}}{\mathrm{16}}\mathrm{sin}\:^{\mathrm{2}} \theta−\mathrm{40sin}\:\theta+\mathrm{16}}\:=\:\mathrm{7}\: \\ $$$$\Rightarrow\:\:\:\boldsymbol{\theta}\approx\:\mathrm{31}.\mathrm{86}°\:\:\:,\:\:\boldsymbol{{x}}\approx\:\mathrm{2}.\mathrm{402}\boldsymbol{{a}} \\ $$
