Question Number 52945 by Tawa1 last updated on 15/Jan/19

Commented by maxmathsup by imad last updated on 15/Jan/19
![3) let A =∫_0 ^∞ ((x ln^2 (x))/(e^x −1)) dx ⇒A =∫_0 ^∞ ((x e^(−x) ln^2 (x))/(1−e^(−x) )) dx =∫_0 ^∞ x e^(−x) ln^2 (x)(Σ_(n=0) ^∞ e^(−nx) )dx =Σ_(n=0) ^∞ ∫_0 ^∞ x e^(−(n+1)x) ln^2 x dx =Σ_(n=0) ^∞ A_n with A_n =∫_0 ^∞ x e^(−(n+1)x) ln^2 (x)dx A_n =_((n+1)x=t) ∫_0 ^∞ (t/(n+1)) e^(−t) ln^2 ((t/(n+1)))(dt/(n+1)) =(1/((n+1)^2 ))∫_0 ^∞ t e^(−t) (ln(t)−ln(n+1))^2 dt ⇒(n+1)^2 A_n =∫_0 ^∞ t e^(−t) (ln^2 (t)−2ln(n+1)ln(t) +ln^2 (n+1))dt =∫_0 ^∞ t e^(−t) ln^2 (t)dt−2ln(n+1)∫_0 ^∞ t e^(−t) ln(t)dt +ln^2 (n+1)∫_0 ^∞ t e^(−t) dt but ∫_0 ^∞ t e^(−t) dt =[−t e^(−t) ]_0 ^(+∞) +∫_0 ^∞ e^(−t) dt =[−e^(−t) ]_0 ^(+∞) =1 by part u^′ =t e^(−t) and v=ln(t) ⇒u =∫ t e^(−t) dt =−t e^(−t) +∫ e^(−t) dt =−t e^(−t) −e^(−t) =−(t+1)e^(−t) +1 ⇒∫_0 ^∞ t e^(−t) ln(t)dt =[(−(t+1)e^(−t) +1)ln(t)]_0 ^(+∞) −∫_0 ^∞ t e^(−t) (dt/t) =−∫_0 ^∞ e^(−t) dt =[e^(−t) ]_0 ^(+∞) =−1 let find ∫_0 ^∞ t e^(−t) ln^2 (t)dt by parts u^′ =t e^(−t) and v=ln^2 (t) ⇒ u =∫ t e^(−t) dt =1−(t+1)e^(−t) ⇒∫_0 ^∞ t e^(−t) ln^2 (t)dt =[(1−(t+1)e^(−t) ln^2 t]_0 ^(+∞) −∫_0 ^∞ t e^(−t) ((2ln(t))/t)dt =−2 ∫_0 ^∞ e^(−t) ln(t)dt =−2(−γ)=2γ ( this result is proved )⇒ (n+1)^2 A_n =2γ +2ln(n+1) +ln^2 (n+1) ⇒ A_n =((2γ)/((n+1)^2 )) + 2((ln(n+1))/((n+1)^2 )) +((ln^2 (n+1))/((n+1)^2 )) ⇒ A =2γ Σ_(n=0) ^∞ (1/((n+1)^2 )) +2Σ_(n=0) ^∞ ((ln(n+1))/((n+1)^2 )) +Σ_(n=0) ^∞ ((ln^2 (n+1))/((n+1)^2 )) Σ_(n=0) ^∞ (1/((n+1)^2 )) =ξ(2)=(π^2 /6) ....becontinued...](https://www.tinkutara.com/question/Q52981.png)
$$\left.\mathrm{3}\right)\:{let}\:{A}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{x}\:{ln}^{\mathrm{2}} \left({x}\right)}{{e}^{{x}} −\mathrm{1}}\:{dx}\:\Rightarrow{A}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{x}\:{e}^{−{x}} {ln}^{\mathrm{2}} \left({x}\right)}{\mathrm{1}−{e}^{−{x}} }\:{dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:{x}\:{e}^{−{x}} {ln}^{\mathrm{2}} \left({x}\right)\left(\sum_{{n}=\mathrm{0}} ^{\infty} \:{e}^{−{nx}} \right){dx}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\int_{\mathrm{0}} ^{\infty} \:{x}\:{e}^{−\left({n}+\mathrm{1}\right){x}} {ln}^{\mathrm{2}} {x}\:{dx} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \:{A}_{{n}} \:\:\:\:{with}\:{A}_{{n}} =\int_{\mathrm{0}} ^{\infty} \:{x}\:{e}^{−\left({n}+\mathrm{1}\right){x}} {ln}^{\mathrm{2}} \left({x}\right){dx} \\ $$$${A}_{{n}} =_{\left({n}+\mathrm{1}\right){x}={t}} \:\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{t}}{{n}+\mathrm{1}}\:{e}^{−{t}} {ln}^{\mathrm{2}} \left(\frac{{t}}{{n}+\mathrm{1}}\right)\frac{{dt}}{{n}+\mathrm{1}}\:=\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }\int_{\mathrm{0}} ^{\infty} \:\:{t}\:{e}^{−{t}} \left({ln}\left({t}\right)−{ln}\left({n}+\mathrm{1}\right)\right)^{\mathrm{2}} {dt} \\ $$$$\Rightarrow\left({n}+\mathrm{1}\right)^{\mathrm{2}} \:{A}_{{n}} =\int_{\mathrm{0}} ^{\infty} \:\:{t}\:{e}^{−{t}} \:\left({ln}^{\mathrm{2}} \left({t}\right)−\mathrm{2}{ln}\left({n}+\mathrm{1}\right){ln}\left({t}\right)\:+{ln}^{\mathrm{2}} \left({n}+\mathrm{1}\right)\right){dt} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\:{t}\:{e}^{−{t}} {ln}^{\mathrm{2}} \left({t}\right){dt}−\mathrm{2}{ln}\left({n}+\mathrm{1}\right)\int_{\mathrm{0}} ^{\infty} \:{t}\:{e}^{−{t}} {ln}\left({t}\right){dt}\:+{ln}^{\mathrm{2}} \left({n}+\mathrm{1}\right)\int_{\mathrm{0}} ^{\infty} \:{t}\:{e}^{−{t}} {dt}\:{but} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:{t}\:{e}^{−{t}} {dt}\:=\left[−{t}\:{e}^{−{t}} \right]_{\mathrm{0}} ^{+\infty} \:+\int_{\mathrm{0}} ^{\infty} \:{e}^{−{t}} {dt}\:=\left[−{e}^{−{t}} \right]_{\mathrm{0}} ^{+\infty} =\mathrm{1} \\ $$$${by}\:{part}\:{u}^{'} \:={t}\:{e}^{−{t}} \:\:{and}\:{v}={ln}\left({t}\right)\:\Rightarrow{u}\:=\int\:{t}\:{e}^{−{t}} {dt}\:=−{t}\:{e}^{−{t}} \:+\int\:\:{e}^{−{t}} {dt} \\ $$$$=−{t}\:{e}^{−{t}} −{e}^{−{t}} \:=−\left({t}+\mathrm{1}\right){e}^{−{t}} +\mathrm{1}\:\Rightarrow\int_{\mathrm{0}} ^{\infty} \:{t}\:{e}^{−{t}} {ln}\left({t}\right){dt} \\ $$$$=\left[\left(−\left({t}+\mathrm{1}\right){e}^{−{t}} +\mathrm{1}\right){ln}\left({t}\right)\right]_{\mathrm{0}} ^{+\infty} \:−\int_{\mathrm{0}} ^{\infty} \:{t}\:{e}^{−{t}} \:\frac{{dt}}{{t}}\:=−\int_{\mathrm{0}} ^{\infty} \:{e}^{−{t}} {dt}\:=\left[{e}^{−{t}} \right]_{\mathrm{0}} ^{+\infty} =−\mathrm{1} \\ $$$${let}\:{find}\:\int_{\mathrm{0}} ^{\infty} \:\:{t}\:{e}^{−{t}} {ln}^{\mathrm{2}} \left({t}\right){dt}\:{by}\:{parts}\:{u}^{'} \:={t}\:{e}^{−{t}} \:{and}\:{v}={ln}^{\mathrm{2}} \left({t}\right)\:\Rightarrow \\ $$$${u}\:=\int\:{t}\:{e}^{−{t}} {dt}\:=\mathrm{1}−\left({t}+\mathrm{1}\right){e}^{−{t}} \:\Rightarrow\int_{\mathrm{0}} ^{\infty} \:{t}\:{e}^{−{t}} {ln}^{\mathrm{2}} \left({t}\right){dt} \\ $$$$=\left[\left(\mathrm{1}−\left({t}+\mathrm{1}\right){e}^{−{t}} {ln}^{\mathrm{2}} {t}\right]_{\mathrm{0}} ^{+\infty} \:−\int_{\mathrm{0}} ^{\infty} \:{t}\:{e}^{−{t}} \:\frac{\mathrm{2}{ln}\left({t}\right)}{{t}}{dt}\right. \\ $$$$=−\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:{e}^{−{t}} {ln}\left({t}\right){dt}\:\:=−\mathrm{2}\left(−\gamma\right)=\mathrm{2}\gamma\:\:\left(\:{this}\:{result}\:{is}\:{proved}\:\right)\Rightarrow \\ $$$$\left({n}+\mathrm{1}\right)^{\mathrm{2}} {A}_{{n}} =\mathrm{2}\gamma\:\:+\mathrm{2}{ln}\left({n}+\mathrm{1}\right)\:+{ln}^{\mathrm{2}} \left({n}+\mathrm{1}\right)\:\Rightarrow \\ $$$${A}_{{n}} =\frac{\mathrm{2}\gamma}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }\:+\:\mathrm{2}\frac{{ln}\left({n}+\mathrm{1}\right)}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }\:+\frac{{ln}^{\mathrm{2}} \left({n}+\mathrm{1}\right)}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$${A}\:=\mathrm{2}\gamma\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }\:+\mathrm{2}\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{ln}\left({n}+\mathrm{1}\right)}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }\:+\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{{ln}^{\mathrm{2}} \left({n}+\mathrm{1}\right)}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }\:=\xi\left(\mathrm{2}\right)=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:\:\:….{becontinued}… \\ $$
Commented by Tawa1 last updated on 15/Jan/19
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir},\:\mathrm{waiting}\:\mathrm{for}\:\mathrm{the}\:\mathrm{rest}\:\mathrm{sir}.\: \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 15/Jan/19
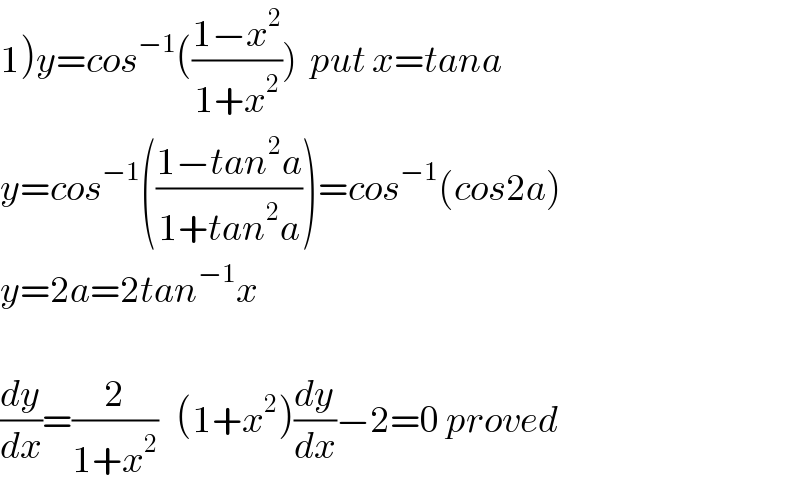
$$\left.\mathrm{1}\right){y}={cos}^{−\mathrm{1}} \left(\frac{\mathrm{1}−{x}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} }\right)\:\:{put}\:{x}={tana} \\ $$$${y}={cos}^{−\mathrm{1}} \left(\frac{\mathrm{1}−{tan}^{\mathrm{2}} {a}}{\mathrm{1}+{tan}^{\mathrm{2}} {a}}\right)={cos}^{−\mathrm{1}} \left({cos}\mathrm{2}{a}\right) \\ $$$${y}=\mathrm{2}{a}=\mathrm{2}{tan}^{−\mathrm{1}} {x} \\ $$$$ \\ $$$$\frac{{dy}}{{dx}}=\frac{\mathrm{2}}{\mathrm{1}+{x}^{\mathrm{2}} }\:\:\:\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\frac{{dy}}{{dx}}−\mathrm{2}=\mathrm{0}\:{proved} \\ $$
Commented by Tawa1 last updated on 15/Jan/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by Tawa1 last updated on 15/Jan/19

$$\mathrm{Please}\:\mathrm{sir},\:\:\:\mathrm{3}\:\mathrm{and}\:\mathrm{5} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 15/Jan/19
![2)cos^(−1) x=a cosa=x sin[cot^(−1) {tana)}] =sin[cot^(−1) {cot((π/2)−a)}] =sin((π/2)−a) =cosa=x proved](https://www.tinkutara.com/question/Q52962.png)
$$\left.\mathrm{2}\right){cos}^{−\mathrm{1}} {x}={a}\:\:{cosa}={x} \\ $$$$\left.{sin}\left[{cot}^{−\mathrm{1}} \left\{{tana}\right)\right\}\right] \\ $$$$={sin}\left[{cot}^{−\mathrm{1}} \left\{{cot}\left(\frac{\pi}{\mathrm{2}}−{a}\right)\right\}\right] \\ $$$$={sin}\left(\frac{\pi}{\mathrm{2}}−{a}\right) \\ $$$$={cosa}={x}\:{proved} \\ $$
Commented by Tawa1 last updated on 15/Jan/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 15/Jan/19
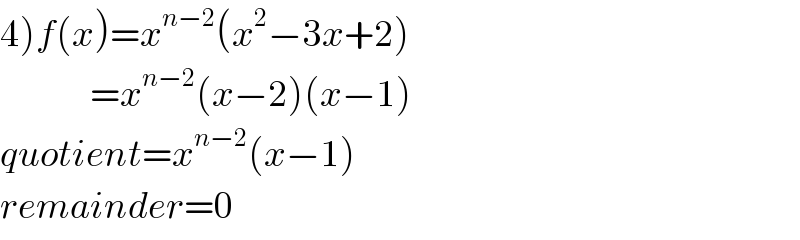
$$\left.\mathrm{4}\right){f}\left({x}\right)={x}^{{n}−\mathrm{2}} \left({x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{2}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:={x}^{{n}−\mathrm{2}} \left({x}−\mathrm{2}\right)\left({x}−\mathrm{1}\right) \\ $$$${quotient}={x}^{{n}−\mathrm{2}} \left({x}−\mathrm{1}\right) \\ $$$${remainder}=\mathrm{0} \\ $$
Commented by Tawa1 last updated on 15/Jan/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
