Question Number 53025 by ajfour last updated on 16/Jan/19

Commented by ajfour last updated on 16/Jan/19

$${Find}\:{minimum}\:{distance}\:{of}\:{line} \\ $$$${AB}\:{from}\:{cylinder}\:{axis}. \\ $$$$\left({correction}:\:{the}\:{shown}\:{segment}\right. \\ $$$${with}\:{which}\:{AB}\:{makes}\:\angle\:\alpha\:{should} \\ $$$$\left.\:{end}\:{in}\:{foot}\:{of}\:{vertical}\:{from}\:{A}.\right) \\ $$$$ \\ $$
Answered by mr W last updated on 16/Jan/19
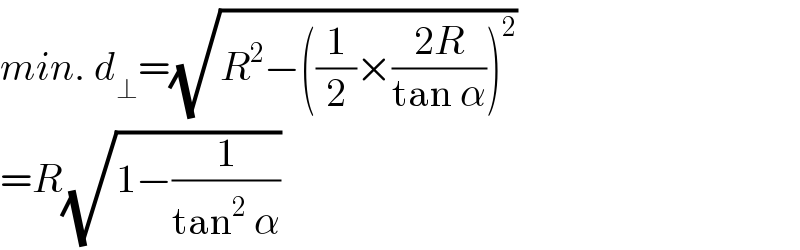
$${min}.\:{d}_{\bot} =\sqrt{{R}^{\mathrm{2}} −\left(\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{2}{R}}{\mathrm{tan}\:\alpha}\right)^{\mathrm{2}} } \\ $$$$={R}\sqrt{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{tan}^{\mathrm{2}} \:\alpha}} \\ $$
Commented by ajfour last updated on 16/Jan/19
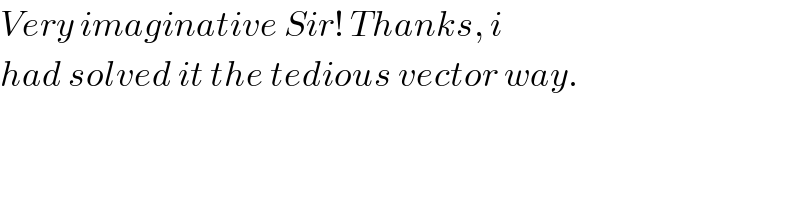
$${Very}\:{imaginative}\:{Sir}!\:{Thanks},\:{i} \\ $$$${had}\:{solved}\:{it}\:{the}\:{tedious}\:{vector}\:{way}. \\ $$
Commented by mr W last updated on 16/Jan/19

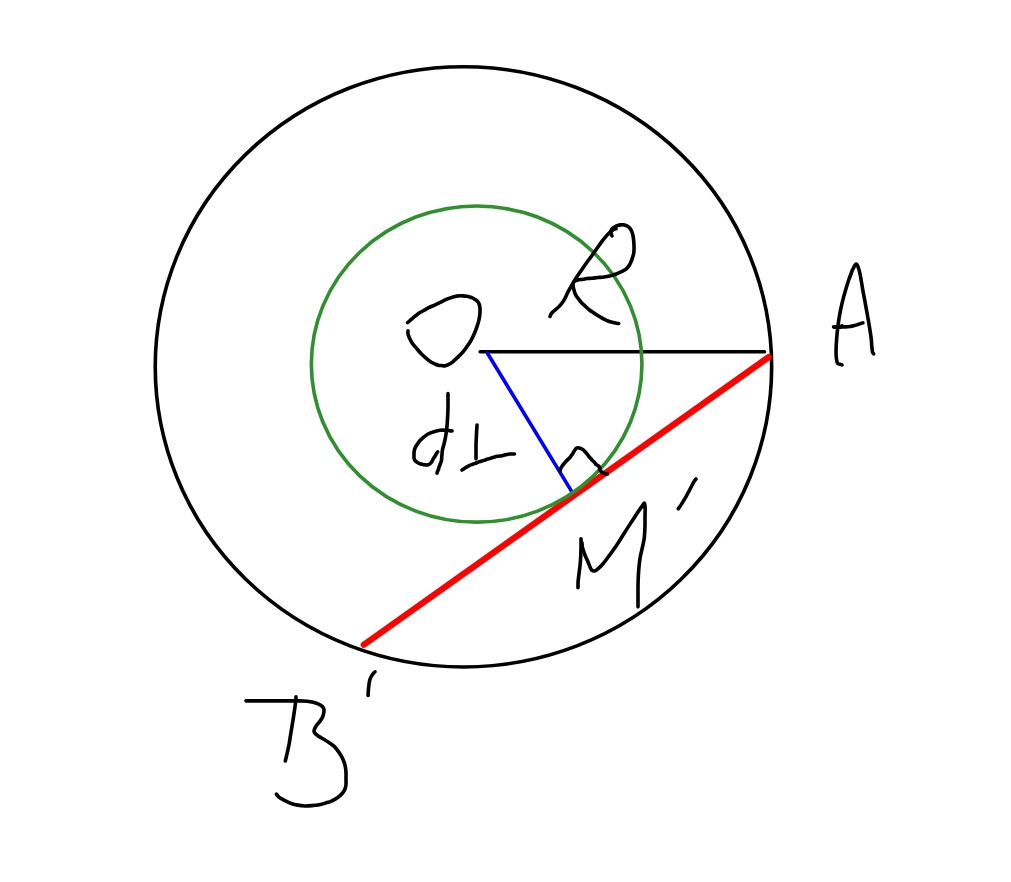
$${construct}\:{a}\:{cylinder}\:{with}\:{the}\:{same} \\ $$$${axis},\:{if}\:{this}\:{cylinder}\:{touches}\:{the}\:{line} \\ $$$${AB}\:{at}\:{only}\:{one}\:{point},\:{then}\:{the}\:{radius}\:{of} \\ $$$${this}\:{cylinder}\:{is}\:{the}\:{minimum}\:{distance} \\ $$$${searched}.\:\:{it}'{s}\:{obvious}\:{that}\:{this}\:{cylinder} \\ $$$${touches}\:{the}\:{line}\:{AB}\:{at}\:{its}\:{midpoint}. \\ $$$${AB}'=\frac{{h}}{\mathrm{tan}\:\alpha}=\frac{\mathrm{2}{R}}{\mathrm{tan}\:\alpha} \\ $$$${AM}'=\frac{{AB}'}{\mathrm{2}}=\frac{{R}}{\mathrm{tan}\:\alpha} \\ $$$${d}_{\bot} ={OM}'=\sqrt{{R}^{\mathrm{2}} −\left(\frac{{R}}{\mathrm{tan}\:\alpha}\right)^{\mathrm{2}} }={R}\sqrt{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{tan}^{\mathrm{2}} \:\alpha}} \\ $$
Commented by ajfour last updated on 16/Jan/19
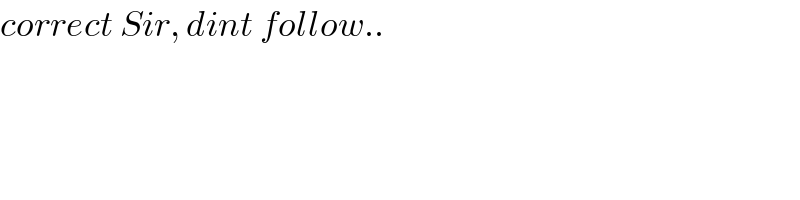
$${correct}\:{Sir},\:{dint}\:{follow}.. \\ $$
Commented by mr W last updated on 16/Jan/19
Commented by Otchere Abdullai last updated on 16/Jan/19
$${wow}!\:{this}\:{man}\:\:{have}\:{creative}\:{mind}\:{his}\: \\ $$$${solutions}\:{are}\:{always}\:{correct}\:{and} \\ $$$${unique} \\ $$
