Question Number 53031 by behi83417@gmail.com last updated on 16/Jan/19
Commented by behi83417@gmail.com last updated on 16/Jan/19
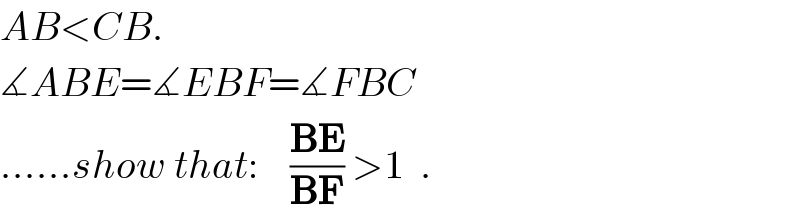
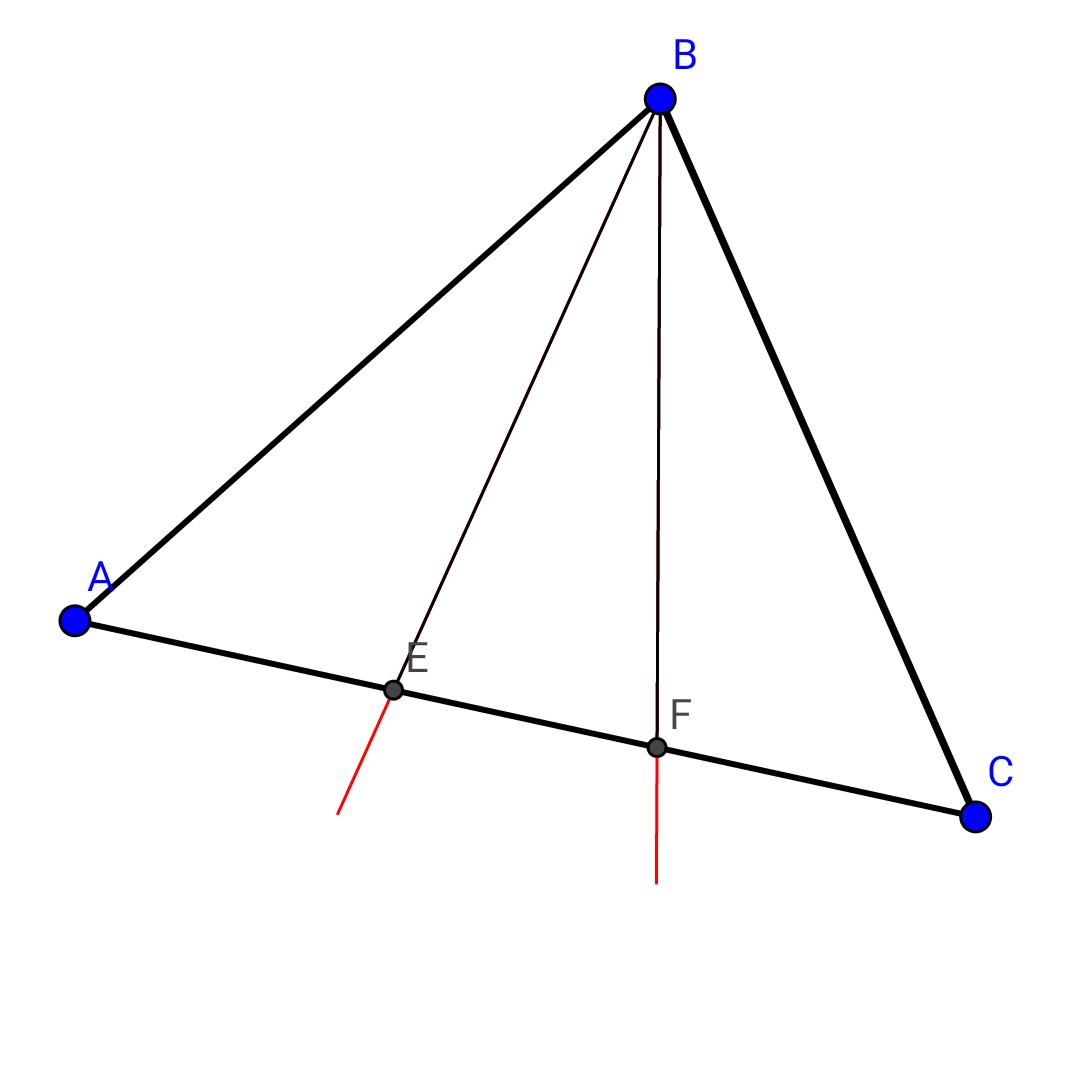
$${AB}<{CB}. \\ $$$$\measuredangle{ABE}=\measuredangle{EBF}=\measuredangle{FBC} \\ $$$$……{show}\:{that}:\:\:\:\:\frac{\boldsymbol{\mathrm{BE}}}{\boldsymbol{\mathrm{BF}}}\:>\mathrm{1}\:\:. \\ $$
Answered by ajfour last updated on 16/Jan/19

$${let}\:{the}\:{three}\:{equal}\:{angles}\:{be}\:\theta. \\ $$$$\frac{{BE}}{\mathrm{sin}\:{A}}\:=\:\frac{{AB}}{\mathrm{sin}\:\angle{AEB}}\:\:\:\:\& \\ $$$$\frac{{BF}}{\mathrm{sin}\:{C}}\:=\:\:\frac{{BC}}{\mathrm{sin}\:\angle{CFB}} \\ $$$$\:{AB}\:<\:{BC}\:\:\:\Rightarrow\:\angle{C}\:<\:\angle{A}\:\Rightarrow\:\:\mathrm{sin}\:{C}\:<\:\mathrm{sin}\:{A} \\ $$$${further} \\ $$$$\:\angle{AEB}+\angle{A}+\theta\:=\:\angle{CFB}+\angle{C}+\theta \\ $$$$\Rightarrow\:\angle{CFB}\:>\:\angle\:{AEB} \\ $$$${from}\:{eqs}.\:{in}\:{first}\:{and}\:{second}\:{line} \\ $$$$\frac{{BE}}{{BF}}\:=\:\frac{\mathrm{sin}\:{A}}{\mathrm{sin}\:{C}}×\frac{\mathrm{sin}\:\angle{CFB}}{\mathrm{sin}\:\angle{AEB}} \\ $$$$\:\:\:\:\:\:\:\:\:=\:\left(>\mathrm{1}\right)×\left(>\mathrm{1}\right)\:>\:\mathrm{1}\: \\ $$$${hence}\:\:{BE}\:>\:{BF}\:. \\ $$
