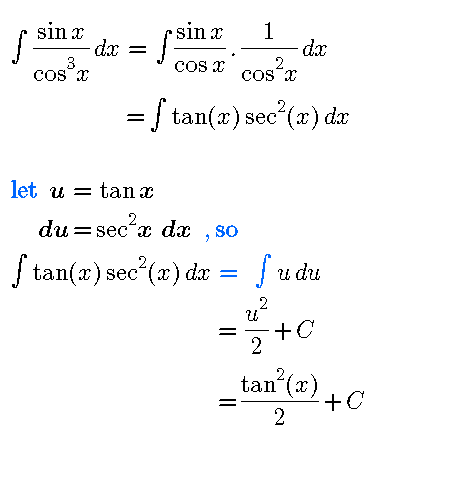Question Number 53081 by cesar.marval.larez@gmail.com last updated on 17/Jan/19

Answered by tanmay.chaudhury50@gmail.com last updated on 17/Jan/19
![1)∫e^(2x) sinxdx e^(2x) ∫sinxdx−∫[((d(e^(2x) ))/dx)∫sinxdx]dx =e^(2x) ×−cosx−∫2e^(2x) (−cosx)dx =−e^(2x) cosx+2∫e^(2x) cosxdx =−e^(2x) cosx+2I_1 I_1 =∫e^(2x) cosxdx =e^(2x) ∫cosxdx−∫[((d(e^(2x) ))/dx)∫cosxdx]dx =e^(2x) sinx−∫2e^(2x) sinxdx =e^(2x) sinx−2I I=−e^(2x) cosx+2I_1 I=−e^(2x) cosx+2(e^(2x) sinx−2I) I=−e^(2x) cosx+2e^(2x) sinx−4I 5I=−e^(2x) cosx+2e^(2x) sinx I=(1/5)(−e^(2x) cosx+2e^(2x) sinx)](https://www.tinkutara.com/question/Q53082.png)
$$\left.\mathrm{1}\right)\int{e}^{\mathrm{2}{x}} {sinxdx} \\ $$$${e}^{\mathrm{2}{x}} \int{sinxdx}−\int\left[\frac{{d}\left({e}^{\mathrm{2}{x}} \right)}{{dx}}\int{sinxdx}\right]{dx} \\ $$$$={e}^{\mathrm{2}{x}} ×−{cosx}−\int\mathrm{2}{e}^{\mathrm{2}{x}} \left(−{cosx}\right){dx} \\ $$$$=−{e}^{\mathrm{2}{x}} {cosx}+\mathrm{2}\int{e}^{\mathrm{2}{x}} {cosxdx} \\ $$$$=−{e}^{\mathrm{2}{x}} {cosx}+\mathrm{2}{I}_{\mathrm{1}} \\ $$$${I}_{\mathrm{1}} =\int{e}^{\mathrm{2}{x}} {cosxdx} \\ $$$$={e}^{\mathrm{2}{x}} \int{cosxdx}−\int\left[\frac{{d}\left({e}^{\mathrm{2}{x}} \right)}{{dx}}\int{cosxdx}\right]{dx} \\ $$$$={e}^{\mathrm{2}{x}} {sinx}−\int\mathrm{2}{e}^{\mathrm{2}{x}} {sinxdx} \\ $$$$={e}^{\mathrm{2}{x}} {sinx}−\mathrm{2}{I} \\ $$$${I}=−{e}^{\mathrm{2}{x}} {cosx}+\mathrm{2}{I}_{\mathrm{1}} \\ $$$${I}=−{e}^{\mathrm{2}{x}} {cosx}+\mathrm{2}\left({e}^{\mathrm{2}{x}} {sinx}−\mathrm{2}{I}\right) \\ $$$${I}=−{e}^{\mathrm{2}{x}} {cosx}+\mathrm{2}{e}^{\mathrm{2}{x}} {sinx}−\mathrm{4}{I} \\ $$$$\mathrm{5}{I}=−{e}^{\mathrm{2}{x}} {cosx}+\mathrm{2}{e}^{\mathrm{2}{x}} {sinx} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{5}}\left(−{e}^{\mathrm{2}{x}} {cosx}+\mathrm{2}{e}^{\mathrm{2}{x}} {sinx}\right) \\ $$
Commented by Otchere Abdullai last updated on 17/Jan/19
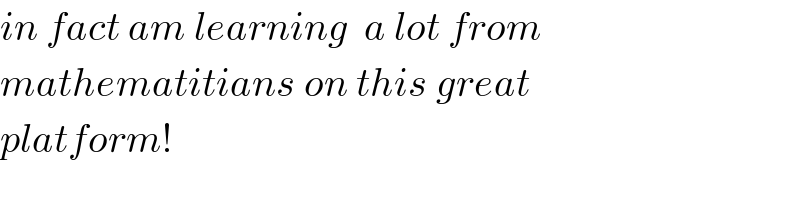
$${in}\:{fact}\:{am}\:{learning}\:\:{a}\:{lot}\:{from} \\ $$$${mathematitians}\:{on}\:{this}\:{great}\: \\ $$$${platform}! \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 17/Jan/19

$${thank}\:{you}… \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 17/Jan/19
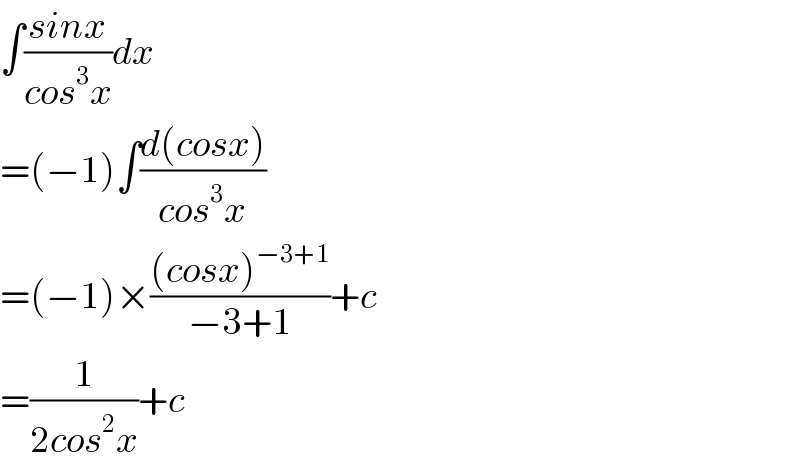
$$\int\frac{{sinx}}{{cos}^{\mathrm{3}} {x}}{dx} \\ $$$$=\left(−\mathrm{1}\right)\int\frac{{d}\left({cosx}\right)}{{cos}^{\mathrm{3}} {x}} \\ $$$$=\left(−\mathrm{1}\right)×\frac{\left({cosx}\right)^{−\mathrm{3}+\mathrm{1}} }{−\mathrm{3}+\mathrm{1}}+{c} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{cos}^{\mathrm{2}} {x}}+{c} \\ $$
Answered by afachri last updated on 17/Jan/19