Menu Close

Question-53168

Tinku Tara 0 Comments
Pin




Question Number 53168 by ajfour last updated on 18/Jan/19
Commented by ajfour last updated on 19/Jan/19
Equilateral △ABC contains two circles of radii a and b in the manner shown. Find the radius R of a circle that touches these two circles externally and passes through vertex A in terms of a and b.
$${Equilateral}\:\bigtriangleup{ABC}\:\:{contains} \\ $$$${two}\:{circles}\:\:{of}\:{radii}\:{a}\:{and}\:{b}\:{in}\:{the} \\ $$$${manner}\:{shown}.\:{Find}\:{the}\:{radius} \\ $$$${R}\:{of}\:{a}\:{circle}\:{that}\:{touches}\:{these}\:{two} \\ $$$${circles}\:{externally}\:{and}\:{passes}\:{through} \\ $$$${vertex}\:{A}\:{in}\:{terms}\:{of}\:\boldsymbol{{a}}\:{and}\:\boldsymbol{{b}}.\:\:\:\:\:\: \\ $$
Commented by behi83417@gmail.com last updated on 18/Jan/19
R=b.((a+b)/(a−b)) ?
$${R}={b}.\frac{{a}+{b}}{{a}−{b}}\:\:? \\ $$
Commented by ajfour last updated on 18/Jan/19
so quick! how do you get it ?
$${so}\:{quick}!\:{how}\:{do}\:{you}\:{get}\:{it}\:? \\ $$
Commented by behi83417@gmail.com last updated on 18/Jan/19
side s is missing in your commonet.
$${side}\:{s}\:{is}\:{missing}\:{in}\:{your}\:{commonet}. \\ $$
Commented by ajfour last updated on 18/Jan/19
s is not even required, solution sir?
$${s}\:{is}\:{not}\:{even}\:{required},\:{solution}\:{sir}? \\ $$
Commented by MJS last updated on 20/Jan/19
s=1∧((√3)/(18))<a<((√3)/6): b=(1/3)((√3)−a−2(√((√3)a−2a^2 ))) for these values both circles stay within the triangle and the big circle exists I haven′t been able to get the coordinates of P or the value of r
$${s}=\mathrm{1}\wedge\frac{\sqrt{\mathrm{3}}}{\mathrm{18}}<{a}<\frac{\sqrt{\mathrm{3}}}{\mathrm{6}}:\:{b}=\frac{\mathrm{1}}{\mathrm{3}}\left(\sqrt{\mathrm{3}}−{a}−\mathrm{2}\sqrt{\sqrt{\mathrm{3}}{a}−\mathrm{2}{a}^{\mathrm{2}} }\right) \\ $$$$\mathrm{for}\:\mathrm{these}\:\mathrm{values}\:\mathrm{both}\:\mathrm{circles}\:\mathrm{stay}\:\mathrm{within}\:\mathrm{the} \\ $$$$\mathrm{triangle}\:\mathrm{and}\:\mathrm{the}\:\mathrm{big}\:\mathrm{circle}\:\mathrm{exists} \\ $$$$\mathrm{I}\:\mathrm{haven}'\mathrm{t}\:\mathrm{been}\:\mathrm{able}\:\mathrm{to}\:\mathrm{get}\:\mathrm{the}\:\mathrm{coordinates} \\ $$$$\mathrm{of}\:{P}\:\mathrm{or}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:{r} \\ $$
Answered by mr W last updated on 19/Jan/19
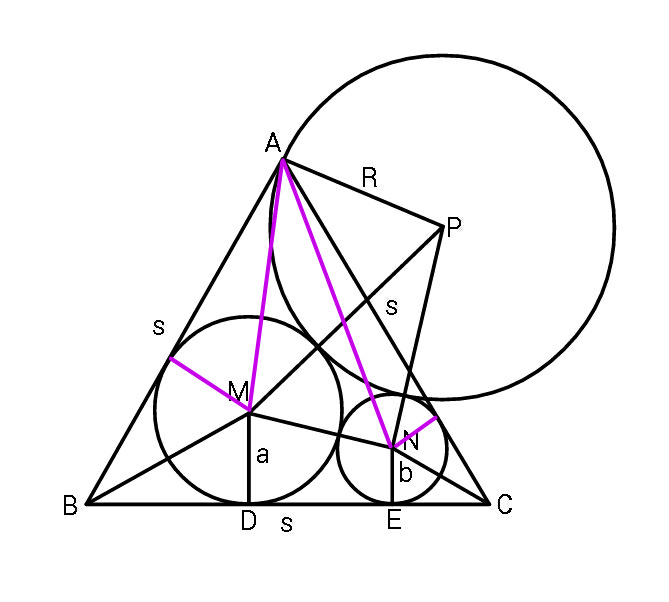
Commented by mr W last updated on 19/Jan/19
s=(√3)(a+b)+(√((a+b)^2 −(a−b)^2 ))=(√3)(a+b)+2(√(ab)) AM=(√((s−(√3)a)^2 +a^2 ))=(√(((√3)b+2(√(ab)))^2 +a^2 ))=(√(a^2 +3b^2 +4ab+4b(√(3ab)))) AN=(√((s−(√3)b)+b^2 ))=(√(3a^2 +b^2 +4ab+4a(√(ab)))) MN=a+b PM=a+R PN=b+R AP=R let ∠APM=α, ∠MPN=β cos α=((R^2 +(R+a)^2 −(a^2 +3b^2 +4ab+4b(√(3ab))))/(2R(R+a))) ⇒cos α=((2R^2 +2aR−3b^2 −4ab−4b(√(3ab)))/(2R(R+a))) cos β=(((R+a)^2 +(R+b)^2 −(a+b)^2 )/(2(R+a)(R+b))) ⇒cos β=((R^2 +(a+b)R−ab)/((R+a)(R+b))) cos (α+β)=((R^2 +(R+b)^2 −(3a^2 +b^2 +4ab+4a(√(ab))))/(2R(R+b))) ⇒cos (α+β)=((2R^2 +2bR−3a^2 −4ab−4a(√(ab)))/(2R(R+b))) ⇒cos^(−1) ((2R^2 +2bR−3a^2 −4ab−4a(√(ab)))/(2R(R+b)))=cos^(−1) ((2R^2 +2aR−3b^2 −4ab−4b(√(3ab)))/(2R(R+a)))+cos^(−1) ((R^2 +(a+b)R−ab)/((R+a)(R+b))) let μ=(b/a), λ=(R/a) ⇒cos^(−1) {1−((3+4μ+4(√μ))/(2λ(λ+μ)))}=cos^(−1) {1−((3μ^2 +4μ+4μ(√(3μ)))/(2λ(λ+1)))}+cos^(−1) {1−((2μ)/((λ+1)(λ+μ)))} ⇒λ=λ(μ)....
$${s}=\sqrt{\mathrm{3}}\left({a}+{b}\right)+\sqrt{\left({a}+{b}\right)^{\mathrm{2}} −\left({a}−{b}\right)^{\mathrm{2}} }=\sqrt{\mathrm{3}}\left({a}+{b}\right)+\mathrm{2}\sqrt{{ab}} \\ $$$${AM}=\sqrt{\left({s}−\sqrt{\mathrm{3}}{a}\right)^{\mathrm{2}} +{a}^{\mathrm{2}} }=\sqrt{\left(\sqrt{\mathrm{3}}{b}+\mathrm{2}\sqrt{{ab}}\right)^{\mathrm{2}} +{a}^{\mathrm{2}} }=\sqrt{{a}^{\mathrm{2}} +\mathrm{3}{b}^{\mathrm{2}} +\mathrm{4}{ab}+\mathrm{4}{b}\sqrt{\mathrm{3}{ab}}} \\ $$$${AN}=\sqrt{\left({s}−\sqrt{\mathrm{3}}{b}\right)+{b}^{\mathrm{2}} }=\sqrt{\mathrm{3}{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{4}{ab}+\mathrm{4}{a}\sqrt{{ab}}} \\ $$$${MN}={a}+{b} \\ $$$${PM}={a}+{R} \\ $$$${PN}={b}+{R} \\ $$$${AP}={R} \\ $$$${let}\:\angle{APM}=\alpha,\:\angle{MPN}=\beta \\ $$$$\mathrm{cos}\:\alpha=\frac{{R}^{\mathrm{2}} +\left({R}+{a}\right)^{\mathrm{2}} −\left({a}^{\mathrm{2}} +\mathrm{3}{b}^{\mathrm{2}} +\mathrm{4}{ab}+\mathrm{4}{b}\sqrt{\mathrm{3}{ab}}\right)}{\mathrm{2}{R}\left({R}+{a}\right)} \\ $$$$\Rightarrow\mathrm{cos}\:\alpha=\frac{\mathrm{2}{R}^{\mathrm{2}} +\mathrm{2}{aR}−\mathrm{3}{b}^{\mathrm{2}} −\mathrm{4}{ab}−\mathrm{4}{b}\sqrt{\mathrm{3}{ab}}}{\mathrm{2}{R}\left({R}+{a}\right)} \\ $$$$\mathrm{cos}\:\beta=\frac{\left({R}+{a}\right)^{\mathrm{2}} +\left({R}+{b}\right)^{\mathrm{2}} −\left({a}+{b}\right)^{\mathrm{2}} }{\mathrm{2}\left({R}+{a}\right)\left({R}+{b}\right)} \\ $$$$\Rightarrow\mathrm{cos}\:\beta=\frac{{R}^{\mathrm{2}} +\left({a}+{b}\right){R}−{ab}}{\left({R}+{a}\right)\left({R}+{b}\right)} \\ $$$$\mathrm{cos}\:\left(\alpha+\beta\right)=\frac{{R}^{\mathrm{2}} +\left({R}+{b}\right)^{\mathrm{2}} −\left(\mathrm{3}{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{4}{ab}+\mathrm{4}{a}\sqrt{{ab}}\right)}{\mathrm{2}{R}\left({R}+{b}\right)} \\ $$$$\Rightarrow\mathrm{cos}\:\left(\alpha+\beta\right)=\frac{\mathrm{2}{R}^{\mathrm{2}} +\mathrm{2}{bR}−\mathrm{3}{a}^{\mathrm{2}} −\mathrm{4}{ab}−\mathrm{4}{a}\sqrt{{ab}}}{\mathrm{2}{R}\left({R}+{b}\right)} \\ $$$$ \\ $$$$\Rightarrow\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{2}{R}^{\mathrm{2}} +\mathrm{2}{bR}−\mathrm{3}{a}^{\mathrm{2}} −\mathrm{4}{ab}−\mathrm{4}{a}\sqrt{{ab}}}{\mathrm{2}{R}\left({R}+{b}\right)}=\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{2}{R}^{\mathrm{2}} +\mathrm{2}{aR}−\mathrm{3}{b}^{\mathrm{2}} −\mathrm{4}{ab}−\mathrm{4}{b}\sqrt{\mathrm{3}{ab}}}{\mathrm{2}{R}\left({R}+{a}\right)}+\mathrm{cos}^{−\mathrm{1}} \frac{{R}^{\mathrm{2}} +\left({a}+{b}\right){R}−{ab}}{\left({R}+{a}\right)\left({R}+{b}\right)} \\ $$$${let}\:\mu=\frac{{b}}{{a}},\:\lambda=\frac{{R}}{{a}} \\ $$$$\Rightarrow\mathrm{cos}^{−\mathrm{1}} \left\{\mathrm{1}−\frac{\mathrm{3}+\mathrm{4}\mu+\mathrm{4}\sqrt{\mu}}{\mathrm{2}\lambda\left(\lambda+\mu\right)}\right\}=\mathrm{cos}^{−\mathrm{1}} \left\{\mathrm{1}−\frac{\mathrm{3}\mu^{\mathrm{2}} +\mathrm{4}\mu+\mathrm{4}\mu\sqrt{\mathrm{3}\mu}}{\mathrm{2}\lambda\left(\lambda+\mathrm{1}\right)}\right\}+\mathrm{cos}^{−\mathrm{1}} \left\{\mathrm{1}−\frac{\mathrm{2}\mu}{\left(\lambda+\mathrm{1}\right)\left(\lambda+\mu\right)}\right\} \\ $$$$\Rightarrow\lambda=\lambda\left(\mu\right)…. \\ $$
Commented by ajfour last updated on 19/Jan/19
Thanks sir, very better way, i had resorted to a coordinate like method.
$${Thanks}\:{sir},\:{very}\:{better}\:{way},\:{i}\:{had} \\ $$$${resorted}\:{to}\:{a}\:{coordinate}\:{like}\:{method}. \\ $$
Answered by ajfour last updated on 19/Jan/19
Commented by ajfour last updated on 19/Jan/19
let midpoint of BC be origin O, with x-axis along BC. M(−(s/2)+a(√3), a) ; N((s/2)−b(√3), b) A(0,((s(√3))/2)) ; s=(√3)(a+b)+2(√(ab)) let P (h,k). As MP = a+R (h+(s/2)−a(√3))^2 +(k−a)^2 =(a+R)^2 As NP = b+R (h−(s/2)+b(√3))^2 +(k−b)^2 =(b+R)^2 as AP = R h^2 +(((s(√3))/2)−k)^2 = R^2 .
$${let}\:{midpoint}\:{of}\:{BC}\:{be}\:{origin}\:{O}, \\ $$$${with}\:{x}-{axis}\:{along}\:{BC}. \\ $$$${M}\left(−\frac{{s}}{\mathrm{2}}+{a}\sqrt{\mathrm{3}},\:{a}\right)\:\:;\:{N}\left(\frac{{s}}{\mathrm{2}}−{b}\sqrt{\mathrm{3}},\:{b}\right) \\ $$$${A}\left(\mathrm{0},\frac{{s}\sqrt{\mathrm{3}}}{\mathrm{2}}\right)\:;\:\:{s}=\sqrt{\mathrm{3}}\left({a}+{b}\right)+\mathrm{2}\sqrt{{ab}} \\ $$$${let}\:\:{P}\:\left({h},{k}\right).\:\:{As}\:{MP}\:=\:{a}+{R} \\ $$$$\left({h}+\frac{{s}}{\mathrm{2}}−{a}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} +\left({k}−{a}\right)^{\mathrm{2}} =\left({a}+{R}\right)^{\mathrm{2}} \\ $$$${As}\:{NP}\:=\:{b}+{R} \\ $$$$\:\left({h}−\frac{{s}}{\mathrm{2}}+{b}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} +\left({k}−{b}\right)^{\mathrm{2}} =\left({b}+{R}\right)^{\mathrm{2}} \\ $$$${as}\:{AP}\:=\:{R} \\ $$$$\:\:\:\:{h}^{\mathrm{2}} +\left(\frac{{s}\sqrt{\mathrm{3}}}{\mathrm{2}}−{k}\right)^{\mathrm{2}} =\:{R}^{\mathrm{2}} \:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *