Question Number 53210 by Tawa1 last updated on 19/Jan/19

Answered by tanmay.chaudhury50@gmail.com last updated on 19/Jan/19
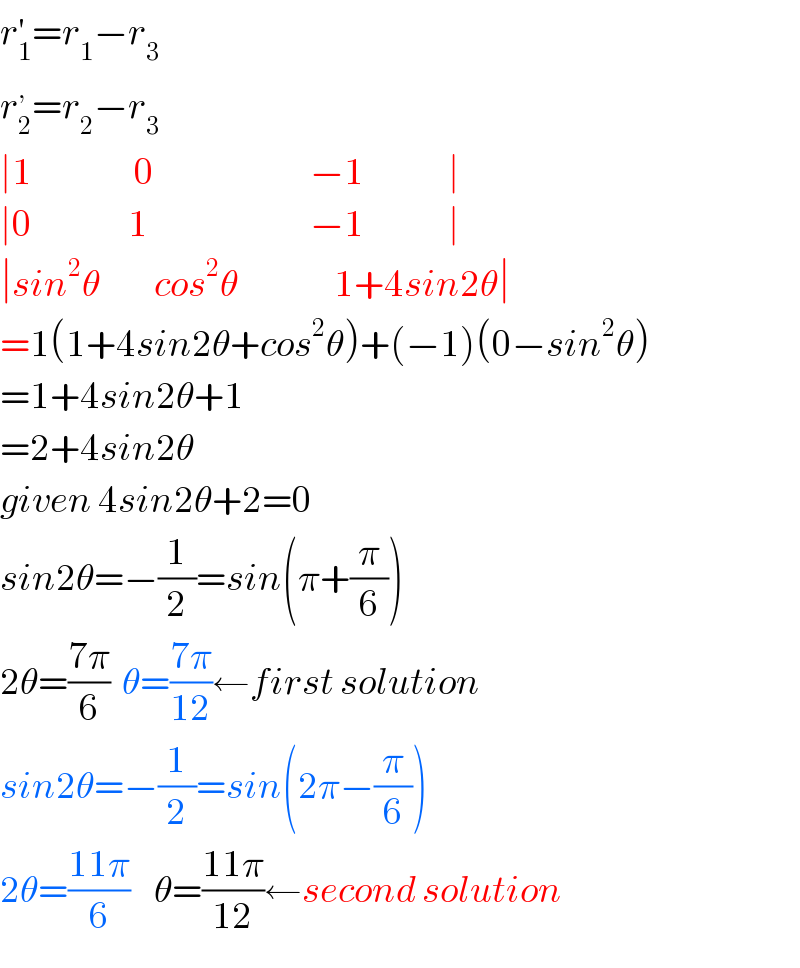
$${r}_{\mathrm{1}} ^{'} ={r}_{\mathrm{1}} −{r}_{\mathrm{3}} \\ $$$${r}_{\mathrm{2}} ^{,} ={r}_{\mathrm{2}} −{r}_{\mathrm{3}} \\ $$$$\mid\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mid \\ $$$$\mid\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mid \\ $$$$\mid{sin}^{\mathrm{2}} \theta\:\:\:\:\:\:\:\:\:{cos}^{\mathrm{2}} \theta\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}+\mathrm{4}{sin}\mathrm{2}\theta\mid \\ $$$$=\mathrm{1}\left(\mathrm{1}+\mathrm{4}{sin}\mathrm{2}\theta+{cos}^{\mathrm{2}} \theta\right)+\left(−\mathrm{1}\right)\left(\mathrm{0}−{sin}^{\mathrm{2}} \theta\right) \\ $$$$=\mathrm{1}+\mathrm{4}{sin}\mathrm{2}\theta+\mathrm{1} \\ $$$$=\mathrm{2}+\mathrm{4}{sin}\mathrm{2}\theta \\ $$$${given}\:\mathrm{4}{sin}\mathrm{2}\theta+\mathrm{2}=\mathrm{0} \\ $$$${sin}\mathrm{2}\theta=−\frac{\mathrm{1}}{\mathrm{2}}={sin}\left(\pi+\frac{\pi}{\mathrm{6}}\right) \\ $$$$\mathrm{2}\theta=\frac{\mathrm{7}\pi}{\mathrm{6}}\:\:\theta=\frac{\mathrm{7}\pi}{\mathrm{12}}\leftarrow{first}\:{solution} \\ $$$${sin}\mathrm{2}\theta=−\frac{\mathrm{1}}{\mathrm{2}}={sin}\left(\mathrm{2}\pi−\frac{\pi}{\mathrm{6}}\right) \\ $$$$\mathrm{2}\theta=\frac{\mathrm{11}\pi}{\mathrm{6}}\:\:\:\:\theta=\frac{\mathrm{11}\pi}{\mathrm{12}}\leftarrow{second}\:{solution} \\ $$
Commented by Tawa1 last updated on 19/Jan/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
