Question-53323

Question Number 53323 by ajfour last updated on 20/Jan/19

Answered by mr W last updated on 20/Jan/19

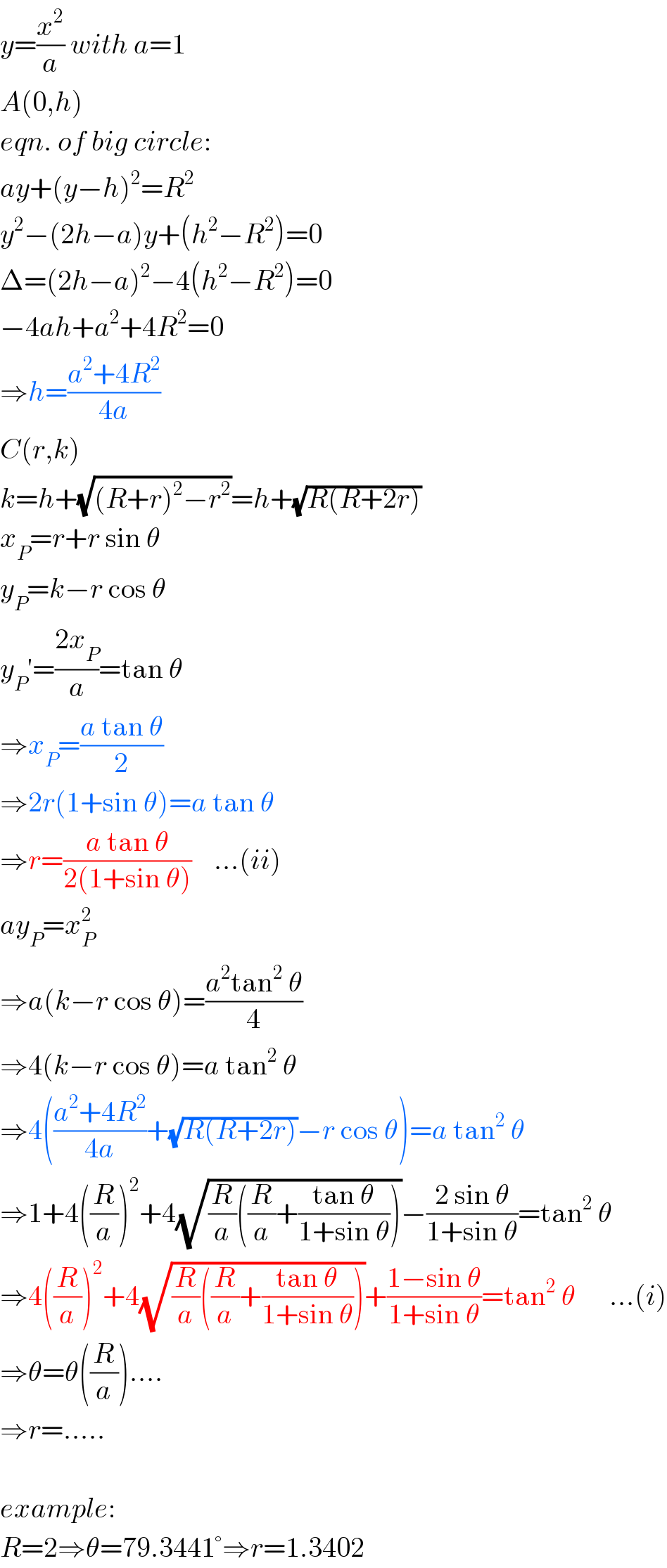
y=(x^2 /a) with a=1 A(0,h) eqn. of big circle: ay+(y−h)^2 =R^2 y^2 −(2h−a)y+(h^2 −R^2 )=0 Δ=(2h−a)^2 −4(h^2 −R^2 )=0 −4ah+a^2 +4R^2 =0 ⇒h=((a^2 +4R^2 )/(4a)) C(r,k) k=h+(√((R+r)^2 −r^2 ))=h+(√(R(R+2r))) x_P =r+r sin θ y_P =k−r cos θ y_P ′=((2x_P )/a)=tan θ ⇒x_P =((a tan θ)/2) ⇒2r(1+sin θ)=a tan θ ⇒r=((a tan θ)/(2(1+sin θ))) ...(ii) ay_P =x_P ^2 ⇒a(k−r cos θ)=((a^2 tan^2 θ)/4) ⇒4(k−r cos θ)=a tan^2 θ ⇒4(((a^2 +4R^2 )/(4a))+(√(R(R+2r)))−r cos θ)=a tan^2 θ ⇒1+4((R/a))^2 +4(√((R/a)((R/a)+((tan θ)/(1+sin θ)))))−((2 sin θ)/(1+sin θ))=tan^2 θ ⇒4((R/a))^2 +4(√((R/a)((R/a)+((tan θ)/(1+sin θ)))))+((1−sin θ)/(1+sin θ))=tan^2 θ ...(i) ⇒θ=θ((R/a)).... ⇒r=..... example: R=2⇒θ=79.3441°⇒r=1.3402

$${y}=\frac{{x}^{\mathrm{2}} }{{a}}\:{with}\:{a}=\mathrm{1} \\ $$$${A}\left(\mathrm{0},{h}\right) \\ $$$${eqn}.\:{of}\:{big}\:{circle}: \\ $$$${ay}+\left({y}−{h}\right)^{\mathrm{2}} ={R}^{\mathrm{2}} \\ $$$${y}^{\mathrm{2}} −\left(\mathrm{2}{h}−{a}\right){y}+\left({h}^{\mathrm{2}} −{R}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\Delta=\left(\mathrm{2}{h}−{a}\right)^{\mathrm{2}} −\mathrm{4}\left({h}^{\mathrm{2}} −{R}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$−\mathrm{4}{ah}+{a}^{\mathrm{2}} +\mathrm{4}{R}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{h}=\frac{{a}^{\mathrm{2}} +\mathrm{4}{R}^{\mathrm{2}} }{\mathrm{4}{a}} \\ $$$${C}\left({r},{k}\right) \\ $$$${k}={h}+\sqrt{\left({R}+{r}\right)^{\mathrm{2}} −{r}^{\mathrm{2}} }={h}+\sqrt{{R}\left({R}+\mathrm{2}{r}\right)} \\ $$$${x}_{{P}} ={r}+{r}\:\mathrm{sin}\:\theta \\ $$$${y}_{{P}} ={k}−{r}\:\mathrm{cos}\:\theta \\ $$$${y}_{{P}} '=\frac{\mathrm{2}{x}_{{P}} }{{a}}=\mathrm{tan}\:\theta \\ $$$$\Rightarrow{x}_{{P}} =\frac{{a}\:\mathrm{tan}\:\theta}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{2}{r}\left(\mathrm{1}+\mathrm{sin}\:\theta\right)={a}\:\mathrm{tan}\:\theta \\ $$$$\Rightarrow{r}=\frac{{a}\:\mathrm{tan}\:\theta}{\mathrm{2}\left(\mathrm{1}+\mathrm{sin}\:\theta\right)}\:\:\:\:…\left({ii}\right) \\ $$$${ay}_{{P}} ={x}_{{P}} ^{\mathrm{2}} \\ $$$$\Rightarrow{a}\left({k}−{r}\:\mathrm{cos}\:\theta\right)=\frac{{a}^{\mathrm{2}} \mathrm{tan}^{\mathrm{2}} \:\theta}{\mathrm{4}} \\ $$$$\Rightarrow\mathrm{4}\left({k}−{r}\:\mathrm{cos}\:\theta\right)={a}\:\mathrm{tan}^{\mathrm{2}} \:\theta \\ $$$$\Rightarrow\mathrm{4}\left(\frac{{a}^{\mathrm{2}} +\mathrm{4}{R}^{\mathrm{2}} }{\mathrm{4}{a}}+\sqrt{{R}\left({R}+\mathrm{2}{r}\right)}−{r}\:\mathrm{cos}\:\theta\right)={a}\:\mathrm{tan}^{\mathrm{2}} \:\theta \\ $$$$\Rightarrow\mathrm{1}+\mathrm{4}\left(\frac{{R}}{{a}}\right)^{\mathrm{2}} +\mathrm{4}\sqrt{\frac{{R}}{{a}}\left(\frac{{R}}{{a}}+\frac{\mathrm{tan}\:\theta}{\mathrm{1}+\mathrm{sin}\:\theta}\right)}−\frac{\mathrm{2}\:\mathrm{sin}\:\theta}{\mathrm{1}+\mathrm{sin}\:\theta}=\mathrm{tan}^{\mathrm{2}} \:\theta \\ $$$$\Rightarrow\mathrm{4}\left(\frac{{R}}{{a}}\right)^{\mathrm{2}} +\mathrm{4}\sqrt{\frac{{R}}{{a}}\left(\frac{{R}}{{a}}+\frac{\mathrm{tan}\:\theta}{\mathrm{1}+\mathrm{sin}\:\theta}\right)}+\frac{\mathrm{1}−\mathrm{sin}\:\theta}{\mathrm{1}+\mathrm{sin}\:\theta}=\mathrm{tan}^{\mathrm{2}} \:\theta\:\:\:\:\:\:…\left({i}\right) \\ $$$$\Rightarrow\theta=\theta\left(\frac{{R}}{{a}}\right)…. \\ $$$$\Rightarrow{r}=….. \\ $$$$ \\ $$$${example}: \\ $$$${R}=\mathrm{2}\Rightarrow\theta=\mathrm{79}.\mathrm{3441}°\Rightarrow{r}=\mathrm{1}.\mathrm{3402} \\ $$

Commented by ajfour last updated on 20/Jan/19

$${Thanks}\:{Sir},\:{very}\:{lucent}\:{manner}! \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply