Question Number 53530 by MJS last updated on 23/Jan/19
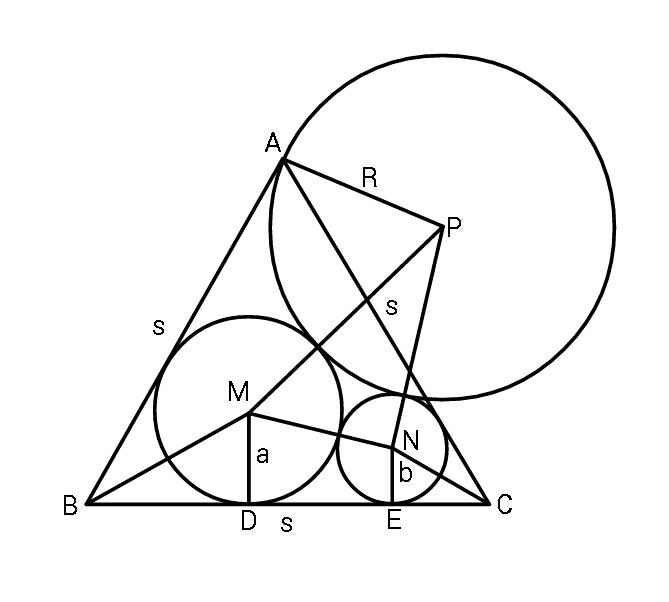
Commented by MJS last updated on 23/Jan/19
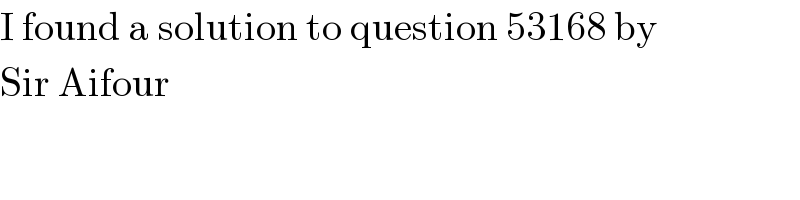
$$\mathrm{I}\:\mathrm{found}\:\mathrm{a}\:\mathrm{solution}\:\mathrm{to}\:\mathrm{question}\:\mathrm{53168}\:\mathrm{by} \\ $$$$\mathrm{Sir}\:\mathrm{Aifour} \\ $$
Answered by MJS last updated on 23/Jan/19
![I changed the setup after some failed attempts I put a=1; b=a^2 ; (1/3)<b≤1 ⇔ ((√3)/3)<a≤1 to go on with b leads to more complications because of terms with (√b^(2n−1) ); the borders for a make sure both circles are within the triangle (we could allow (1/3)<b<3 leading to symmetric results) M= (((−1)),(0) ) N= ((a^2 ),(0) ) the given circles (x+1)^2 +y^2 =1 (x−a^2 )^2 +y^2 =a^4 now it′s possible to get the equations of the lines BC, CA & AB: BC: y=((1−a^2 )/(2a))x−a CA: ((a^2 +2(√3)a−1)/( (√3)a^2 −2a−(√3)))x−((a^2 ((√3)a+1))/(a−(√3))) AB: −(((√3)a^2 −6a−(√3))/(3a^2 +2(√3)a−3))x+(((√3)a+3)/(3a−(√3))) A= (((((a−1)(a+1)(3a^2 +4(√3)a+3))/(2(a^2 +1)))),((−((3(√3)a^5 −15a^4 −14(√3)a^3 +6a^2 +7(√3)a−3)/(2(3a−(√3))(a^2 +1))))) ) B= (((−((2a(a+(√3)))/(a^2 +1)))),((((√3)((√3)a−3)((√3)a+1))/(3(a^2 +1)))) ) C= ((((2a^2 ((√3)a+1))/(a^2 +1))),((−((a^2 ((√3)a^2 +2a−(√3)))/(a^2 +1)))) ) [the roots of 3(√3)a^5 −15a^4 −14(√3)a^3 +6a^2 +7(√3)a−3: a_1 =((√3)/3); a_(2, 3) =((√3)/3)(1+(√7)±(√(5+2(√7)))); a_(4, 5) =((√3)/3)(1−(√7)±(√(−5+2(√7)))i)] the side of the triangle s=(√3)a^2 +2a+(√3) the searched circle can be found like this P= ((p),(q) ) (x−p)^2 +(y−q)^2 =r^2 steps 1 & 2: intersect with the given circles so that there′s exactly one common point with each of them ⇒ p, q step 3: A∈circle ⇒ r these steps lead to 2 solutions, one of the found circles includes the given circles. the hardest work is to simplify the polynomes I spent a day searching for zeros... p=−((a^2 −1)/(a^2 +1))r q=((2a(√(r^2 +(a^2 +1)r)))/(a^2 +1)) r=−((9(a^2 +(((√3)/6)+((√(11))/2))a+1)^2 (a^2 +(((√3)/6)−((√(11))/2))a+1)^2 )/((a−(√3))(a+(√3))((√3)a−1)((√3)a+1)(3a^2 +2(√3)a+3))) isn′t it of a strange but great beauty?](https://www.tinkutara.com/question/Q53534.png)
$$\mathrm{I}\:\mathrm{changed}\:\mathrm{the}\:\mathrm{setup}\:\mathrm{after}\:\mathrm{some}\:\mathrm{failed}\:\mathrm{attempts} \\ $$$$\mathrm{I}\:\mathrm{put}\:{a}=\mathrm{1};\:{b}={a}^{\mathrm{2}} ;\:\frac{\mathrm{1}}{\mathrm{3}}<{b}\leqslant\mathrm{1}\:\Leftrightarrow\:\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}<{a}\leqslant\mathrm{1} \\ $$$$\mathrm{to}\:\mathrm{go}\:\mathrm{on}\:\mathrm{with}\:{b}\:\mathrm{leads}\:\mathrm{to}\:\mathrm{more}\:\mathrm{complications} \\ $$$$\mathrm{because}\:\mathrm{of}\:\mathrm{terms}\:\mathrm{with}\:\sqrt{{b}^{\mathrm{2}{n}−\mathrm{1}} };\:\mathrm{the}\:\mathrm{borders} \\ $$$$\mathrm{for}\:{a}\:\mathrm{make}\:\mathrm{sure}\:\mathrm{both}\:\mathrm{circles}\:\mathrm{are}\:\mathrm{within}\:\mathrm{the} \\ $$$$\mathrm{triangle}\:\left(\mathrm{we}\:\mathrm{could}\:\mathrm{allow}\:\frac{\mathrm{1}}{\mathrm{3}}<{b}<\mathrm{3}\:\mathrm{leading}\:\mathrm{to}\right. \\ $$$$\left.\mathrm{symmetric}\:\mathrm{results}\right) \\ $$$${M}=\begin{pmatrix}{−\mathrm{1}}\\{\mathrm{0}}\end{pmatrix}\:\:{N}=\begin{pmatrix}{{a}^{\mathrm{2}} }\\{\mathrm{0}}\end{pmatrix} \\ $$$$\mathrm{the}\:\mathrm{given}\:\mathrm{circles} \\ $$$$\left({x}+\mathrm{1}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{1} \\ $$$$\left({x}−{a}^{\mathrm{2}} \right)^{\mathrm{2}} +{y}^{\mathrm{2}} ={a}^{\mathrm{4}} \\ $$$$\mathrm{now}\:\mathrm{it}'\mathrm{s}\:\mathrm{possible}\:\mathrm{to}\:\mathrm{get}\:\mathrm{the}\:\mathrm{equations}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{lines}\:{BC},\:{CA}\:\&\:{AB}: \\ $$$${BC}:\:{y}=\frac{\mathrm{1}−{a}^{\mathrm{2}} }{\mathrm{2}{a}}{x}−{a} \\ $$$${CA}:\:\frac{{a}^{\mathrm{2}} +\mathrm{2}\sqrt{\mathrm{3}}{a}−\mathrm{1}}{\:\sqrt{\mathrm{3}}{a}^{\mathrm{2}} −\mathrm{2}{a}−\sqrt{\mathrm{3}}}{x}−\frac{{a}^{\mathrm{2}} \left(\sqrt{\mathrm{3}}{a}+\mathrm{1}\right)}{{a}−\sqrt{\mathrm{3}}} \\ $$$${AB}:\:−\frac{\sqrt{\mathrm{3}}{a}^{\mathrm{2}} −\mathrm{6}{a}−\sqrt{\mathrm{3}}}{\mathrm{3}{a}^{\mathrm{2}} +\mathrm{2}\sqrt{\mathrm{3}}{a}−\mathrm{3}}{x}+\frac{\sqrt{\mathrm{3}}{a}+\mathrm{3}}{\mathrm{3}{a}−\sqrt{\mathrm{3}}} \\ $$$${A}=\begin{pmatrix}{\frac{\left({a}−\mathrm{1}\right)\left({a}+\mathrm{1}\right)\left(\mathrm{3}{a}^{\mathrm{2}} +\mathrm{4}\sqrt{\mathrm{3}}{a}+\mathrm{3}\right)}{\mathrm{2}\left({a}^{\mathrm{2}} +\mathrm{1}\right)}}\\{−\frac{\mathrm{3}\sqrt{\mathrm{3}}{a}^{\mathrm{5}} −\mathrm{15}{a}^{\mathrm{4}} −\mathrm{14}\sqrt{\mathrm{3}}{a}^{\mathrm{3}} +\mathrm{6}{a}^{\mathrm{2}} +\mathrm{7}\sqrt{\mathrm{3}}{a}−\mathrm{3}}{\mathrm{2}\left(\mathrm{3}{a}−\sqrt{\mathrm{3}}\right)\left({a}^{\mathrm{2}} +\mathrm{1}\right)}}\end{pmatrix} \\ $$$${B}=\begin{pmatrix}{−\frac{\mathrm{2}{a}\left({a}+\sqrt{\mathrm{3}}\right)}{{a}^{\mathrm{2}} +\mathrm{1}}}\\{\frac{\sqrt{\mathrm{3}}\left(\sqrt{\mathrm{3}}{a}−\mathrm{3}\right)\left(\sqrt{\mathrm{3}}{a}+\mathrm{1}\right)}{\mathrm{3}\left({a}^{\mathrm{2}} +\mathrm{1}\right)}}\end{pmatrix} \\ $$$${C}=\begin{pmatrix}{\frac{\mathrm{2}{a}^{\mathrm{2}} \left(\sqrt{\mathrm{3}}{a}+\mathrm{1}\right)}{{a}^{\mathrm{2}} +\mathrm{1}}}\\{−\frac{{a}^{\mathrm{2}} \left(\sqrt{\mathrm{3}}{a}^{\mathrm{2}} +\mathrm{2}{a}−\sqrt{\mathrm{3}}\right)}{{a}^{\mathrm{2}} +\mathrm{1}}}\end{pmatrix} \\ $$$$\:\:\:\:\:\:\:\:\:\:\left[\mathrm{the}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{3}\sqrt{\mathrm{3}}{a}^{\mathrm{5}} −\mathrm{15}{a}^{\mathrm{4}} −\mathrm{14}\sqrt{\mathrm{3}}{a}^{\mathrm{3}} +\mathrm{6}{a}^{\mathrm{2}} +\mathrm{7}\sqrt{\mathrm{3}}{a}−\mathrm{3}:\right. \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:{a}_{\mathrm{1}} =\frac{\sqrt{\mathrm{3}}}{\mathrm{3}};\:{a}_{\mathrm{2},\:\mathrm{3}} =\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\left(\mathrm{1}+\sqrt{\mathrm{7}}\pm\sqrt{\mathrm{5}+\mathrm{2}\sqrt{\mathrm{7}}}\right);\:{a}_{\mathrm{4},\:\mathrm{5}} =\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\left(\mathrm{1}−\sqrt{\mathrm{7}}\pm\sqrt{−\mathrm{5}+\mathrm{2}\sqrt{\mathrm{7}}}\mathrm{i}\right)\right] \\ $$$$\mathrm{the}\:\mathrm{side}\:\mathrm{of}\:\mathrm{the}\:\mathrm{triangle} \\ $$$${s}=\sqrt{\mathrm{3}}{a}^{\mathrm{2}} +\mathrm{2}{a}+\sqrt{\mathrm{3}} \\ $$$$\mathrm{the}\:\mathrm{searched}\:\mathrm{circle}\:\mathrm{can}\:\mathrm{be}\:\mathrm{found}\:\mathrm{like}\:\mathrm{this} \\ $$$${P}=\begin{pmatrix}{{p}}\\{{q}}\end{pmatrix} \\ $$$$\left({x}−{p}\right)^{\mathrm{2}} +\left({y}−{q}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\mathrm{steps}\:\mathrm{1}\:\&\:\mathrm{2}:\:\mathrm{intersect}\:\mathrm{with}\:\mathrm{the}\:\mathrm{given}\:\mathrm{circles} \\ $$$$\mathrm{so}\:\mathrm{that}\:\mathrm{there}'\mathrm{s}\:\mathrm{exactly}\:\mathrm{one}\:\mathrm{common}\:\mathrm{point} \\ $$$$\mathrm{with}\:\mathrm{each}\:\mathrm{of}\:\mathrm{them}\:\Rightarrow\:{p},\:{q} \\ $$$$\mathrm{step}\:\mathrm{3}:\:{A}\in\mathrm{circle}\:\Rightarrow\:{r} \\ $$$$\mathrm{these}\:\mathrm{steps}\:\mathrm{lead}\:\mathrm{to}\:\mathrm{2}\:\mathrm{solutions},\:\mathrm{one}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{found}\:\mathrm{circles}\:{includes}\:\mathrm{the}\:\mathrm{given}\:\mathrm{circles}. \\ $$$$\mathrm{the}\:\mathrm{hardest}\:\mathrm{work}\:\mathrm{is}\:\mathrm{to}\:\mathrm{simplify}\:\mathrm{the}\:\mathrm{polynomes} \\ $$$$\mathrm{I}\:\mathrm{spent}\:\mathrm{a}\:\mathrm{day}\:\mathrm{searching}\:\mathrm{for}\:\mathrm{zeros}… \\ $$$${p}=−\frac{{a}^{\mathrm{2}} −\mathrm{1}}{{a}^{\mathrm{2}} +\mathrm{1}}{r} \\ $$$${q}=\frac{\mathrm{2}{a}\sqrt{{r}^{\mathrm{2}} +\left({a}^{\mathrm{2}} +\mathrm{1}\right){r}}}{{a}^{\mathrm{2}} +\mathrm{1}} \\ $$$${r}=−\frac{\mathrm{9}\left({a}^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{6}}+\frac{\sqrt{\mathrm{11}}}{\mathrm{2}}\right){a}+\mathrm{1}\right)^{\mathrm{2}} \left({a}^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{6}}−\frac{\sqrt{\mathrm{11}}}{\mathrm{2}}\right){a}+\mathrm{1}\right)^{\mathrm{2}} }{\left({a}−\sqrt{\mathrm{3}}\right)\left({a}+\sqrt{\mathrm{3}}\right)\left(\sqrt{\mathrm{3}}{a}−\mathrm{1}\right)\left(\sqrt{\mathrm{3}}{a}+\mathrm{1}\right)\left(\mathrm{3}{a}^{\mathrm{2}} +\mathrm{2}\sqrt{\mathrm{3}}{a}+\mathrm{3}\right)} \\ $$$$\mathrm{isn}'\mathrm{t}\:\mathrm{it}\:\mathrm{of}\:\mathrm{a}\:\mathrm{strange}\:\mathrm{but}\:\mathrm{great}\:\mathrm{beauty}? \\ $$
Commented by ajfour last updated on 23/Jan/19
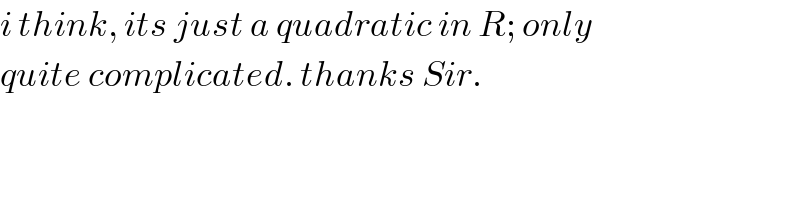
$${i}\:{think},\:{its}\:{just}\:{a}\:{quadratic}\:{in}\:{R};\:{only}\: \\ $$$${quite}\:{complicated}.\:{thanks}\:{Sir}. \\ $$
Commented by MJS last updated on 23/Jan/19

$$\mathrm{it}\:\mathrm{is}\:\mathrm{indeed}\:\mathrm{quadratic}\:\mathrm{in}\:{r}\:\left(\mathrm{your}\:{R}\right)\:\mathrm{but}\:\mathrm{it}'\mathrm{s} \\ $$$$\mathrm{very}\:\mathrm{complicated}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{because}\:\mathrm{it}'\mathrm{s}\:\mathrm{degree} \\ $$$$\mathrm{12}\:\mathrm{in}\:{a}\:\mathrm{and}\:\mathrm{we}\:\mathrm{must}\:\mathrm{constantly}\:\mathrm{find}\:\mathrm{zeros} \\ $$$$\mathrm{to}\:\mathrm{shorten}\:\mathrm{huge}\:\mathrm{fractions}.\:\mathrm{in}\:\mathrm{the}\:\mathrm{end} \\ $$$$\mathrm{everything}\:\mathrm{is}\:\mathrm{fine}.\:\mathrm{even}\:\mathrm{the}\:\mathrm{root}\:\mathrm{in}\:\mathrm{my} \\ $$$${q}\:\mathrm{vanishes}\:\mathrm{because}\:\mathrm{it}'\mathrm{s}\:\sqrt{{term}\left({a}\right)^{\mathrm{2}} }…\:\mathrm{I}'\mathrm{ll} \\ $$$$\mathrm{post}\:\mathrm{later} \\ $$
Answered by ajfour last updated on 23/Jan/19
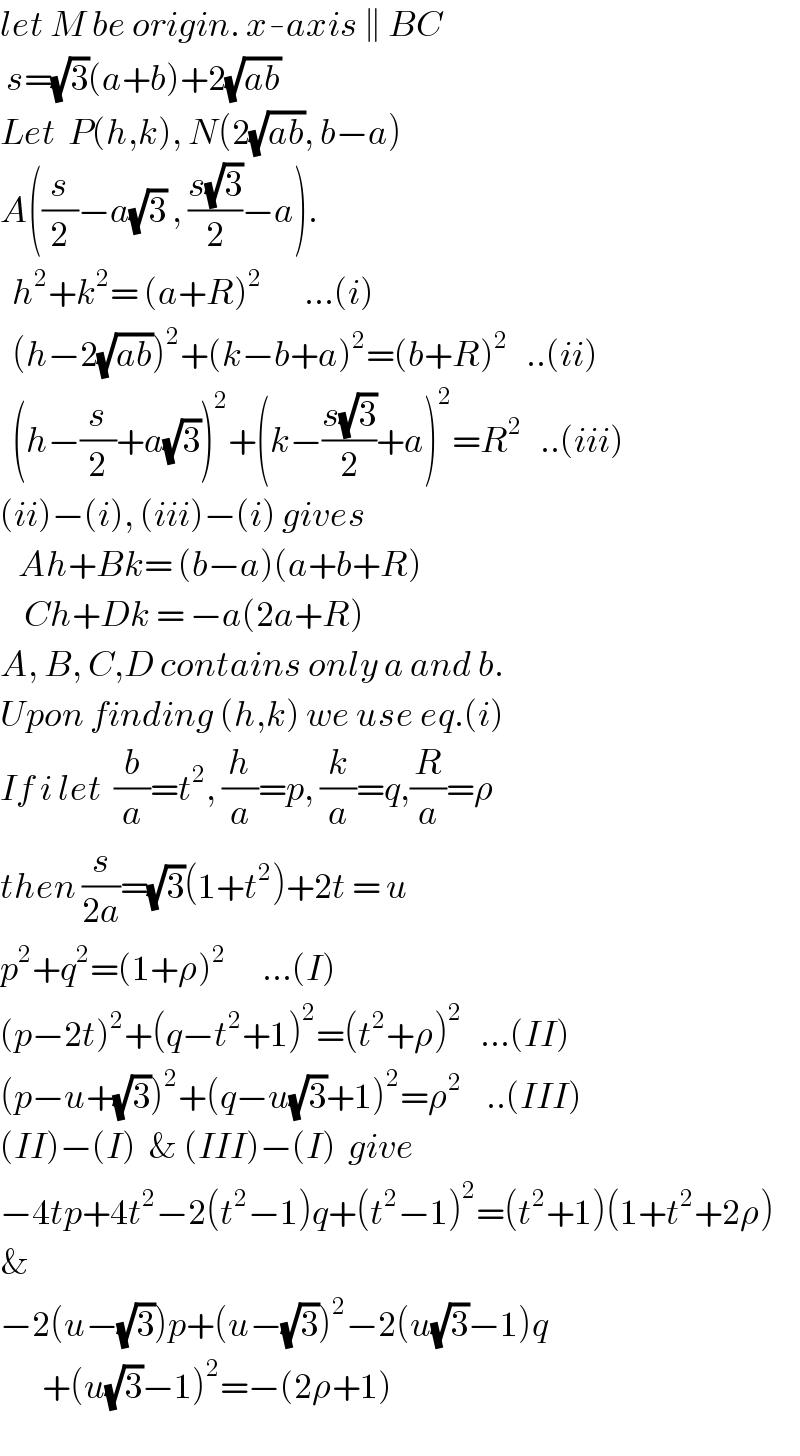
$${let}\:{M}\:{be}\:{origin}.\:{x}-{axis}\:\parallel\:{BC} \\ $$$$\:{s}=\sqrt{\mathrm{3}}\left({a}+{b}\right)+\mathrm{2}\sqrt{{ab}} \\ $$$${Let}\:\:{P}\left({h},{k}\right),\:{N}\left(\mathrm{2}\sqrt{{ab}},\:{b}−{a}\right) \\ $$$${A}\left(\frac{{s}}{\mathrm{2}}−{a}\sqrt{\mathrm{3}}\:,\:\frac{{s}\sqrt{\mathrm{3}}}{\mathrm{2}}−{a}\right). \\ $$$$\:\:{h}^{\mathrm{2}} +{k}^{\mathrm{2}} =\:\left({a}+{R}\right)^{\mathrm{2}} \:\:\:\:\:\:\:…\left({i}\right) \\ $$$$\:\:\left({h}−\mathrm{2}\sqrt{{ab}}\right)^{\mathrm{2}} +\left({k}−{b}+{a}\right)^{\mathrm{2}} =\left({b}+{R}\right)^{\mathrm{2}} \:\:\:..\left({ii}\right) \\ $$$$\:\:\left({h}−\frac{{s}}{\mathrm{2}}+{a}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} +\left({k}−\frac{{s}\sqrt{\mathrm{3}}}{\mathrm{2}}+{a}\right)^{\mathrm{2}} ={R}^{\mathrm{2}} \:\:\:..\left({iii}\right) \\ $$$$\left({ii}\right)−\left({i}\right),\:\left({iii}\right)−\left({i}\right)\:{gives} \\ $$$$\:\:\:{Ah}+{Bk}=\:\left({b}−{a}\right)\left({a}+{b}+{R}\right) \\ $$$$\:\:\:\:{Ch}+{Dk}\:=\:−{a}\left(\mathrm{2}{a}+{R}\right) \\ $$$${A},\:{B},\:{C},{D}\:{contains}\:{only}\:{a}\:{and}\:{b}. \\ $$$${Upon}\:{finding}\:\left({h},{k}\right)\:{we}\:{use}\:{eq}.\left({i}\right) \\ $$$${If}\:{i}\:{let}\:\:\frac{{b}}{{a}}={t}^{\mathrm{2}} ,\:\frac{{h}}{{a}}={p},\:\frac{{k}}{{a}}={q},\frac{{R}}{{a}}=\rho \\ $$$${then}\:\frac{{s}}{\mathrm{2}{a}}=\sqrt{\mathrm{3}}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)+\mathrm{2}{t}\:=\:{u} \\ $$$${p}^{\mathrm{2}} +{q}^{\mathrm{2}} =\left(\mathrm{1}+\rho\right)^{\mathrm{2}} \:\:\:\:\:\:…\left({I}\right) \\ $$$$\left({p}−\mathrm{2}{t}\right)^{\mathrm{2}} +\left({q}−{t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} =\left({t}^{\mathrm{2}} +\rho\right)^{\mathrm{2}} \:\:\:…\left({II}\right) \\ $$$$\left({p}−{u}+\sqrt{\mathrm{3}}\right)^{\mathrm{2}} +\left({q}−{u}\sqrt{\mathrm{3}}+\mathrm{1}\right)^{\mathrm{2}} =\rho^{\mathrm{2}} \:\:\:\:..\left({III}\right) \\ $$$$\left({II}\right)−\left({I}\right)\:\:\&\:\left({III}\right)−\left({I}\right)\:\:{give} \\ $$$$−\mathrm{4}{tp}+\mathrm{4}{t}^{\mathrm{2}} −\mathrm{2}\left({t}^{\mathrm{2}} −\mathrm{1}\right){q}+\left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} =\left({t}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{1}+{t}^{\mathrm{2}} +\mathrm{2}\rho\right) \\ $$$$\& \\ $$$$−\mathrm{2}\left({u}−\sqrt{\mathrm{3}}\right){p}+\left({u}−\sqrt{\mathrm{3}}\right)^{\mathrm{2}} −\mathrm{2}\left({u}\sqrt{\mathrm{3}}−\mathrm{1}\right){q} \\ $$$$\:\:\:\:\:\:\:+\left({u}\sqrt{\mathrm{3}}−\mathrm{1}\right)^{\mathrm{2}} =−\left(\mathrm{2}\rho+\mathrm{1}\right) \\ $$
