Menu Close

Question-53684

Tinku Tara 0 Comments
Pin




Question Number 53684 by ajfour last updated on 25/Jan/19
Commented by ajfour last updated on 25/Jan/19
ceiling to floor height is h.
$${ceiling}\:{to}\:{floor}\:{height}\:{is}\:\boldsymbol{{h}}. \\ $$
Commented by mr W last updated on 25/Jan/19
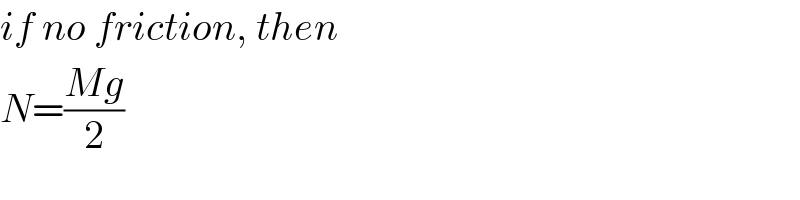
if no friction, then N=((Mg)/2)
$${if}\:{no}\:{friction},\:{then} \\ $$$${N}=\frac{{Mg}}{\mathrm{2}} \\ $$
Commented by mr W last updated on 25/Jan/19
Commented by ajfour last updated on 25/Jan/19
thanks for the tolerance, Sir!
$${thanks}\:{for}\:{the}\:{tolerance},\:{Sir}! \\ $$
Answered by mr W last updated on 25/Jan/19
Commented by mr W last updated on 25/Jan/19
assume μ=friction on ground a sin α+b sin β=h ⇒sin α=((h−b sin β)/a) ⇒cos α=((√(a^2 −(h−b sin β)^2 ))/a) f=μN N b cos β=Mg ((b cos β)/2)+f b sin β ⇒(1−μ tan β)N=((Mg)/2) N (b cos β−a cos α)+mg((a cos α)/2)=Mg (((b cos β)/2)−a cos α)+fh 2N(b cos β−a cos α−μh)=Mgb cos β−(2M+m)ga cos α ((Mg)/(1−μ tan β))(b cos β−a cos α−μh)=Mgb cos β−(2M+m)ga cos α (1/(1−μ tan β))(b cos β−a cos α−μh)=b cos β−(2+(m/M))a cos α ((b cos β−μh)/(1−μ tan β))=b cos β−(2+(m/M)−(1/(1−μ tan β)))a cos α ⇒((μ(h−b sin β))/(1−μ tan β))=(2+(m/M)−(1/(1−μ tan β)))(√(a^2 −(h−b sin β)^2 )) ⇒β=.... ⇒N=((Mg)/(2(1−μ tan β)))
$${assume}\:\mu={friction}\:{on}\:{ground} \\ $$$${a}\:\mathrm{sin}\:\alpha+{b}\:\mathrm{sin}\:\beta={h} \\ $$$$\Rightarrow\mathrm{sin}\:\alpha=\frac{{h}−{b}\:\mathrm{sin}\:\beta}{{a}} \\ $$$$\Rightarrow\mathrm{cos}\:\alpha=\frac{\sqrt{{a}^{\mathrm{2}} −\left({h}−{b}\:\mathrm{sin}\:\beta\right)^{\mathrm{2}} }}{{a}} \\ $$$${f}=\mu{N} \\ $$$${N}\:{b}\:\mathrm{cos}\:\beta={Mg}\:\frac{{b}\:\mathrm{cos}\:\beta}{\mathrm{2}}+{f}\:{b}\:\mathrm{sin}\:\beta \\ $$$$\Rightarrow\left(\mathrm{1}−\mu\:\mathrm{tan}\:\beta\right){N}=\frac{{Mg}}{\mathrm{2}} \\ $$$${N}\:\left({b}\:\mathrm{cos}\:\beta−{a}\:\mathrm{cos}\:\alpha\right)+{mg}\frac{{a}\:\mathrm{cos}\:\alpha}{\mathrm{2}}={Mg}\:\left(\frac{{b}\:\mathrm{cos}\:\beta}{\mathrm{2}}−{a}\:\mathrm{cos}\:\alpha\right)+{fh} \\ $$$$\mathrm{2}{N}\left({b}\:\mathrm{cos}\:\beta−{a}\:\mathrm{cos}\:\alpha−\mu{h}\right)={Mgb}\:\mathrm{cos}\:\beta−\left(\mathrm{2}{M}+{m}\right){ga}\:\mathrm{cos}\:\alpha \\ $$$$\frac{{Mg}}{\mathrm{1}−\mu\:\mathrm{tan}\:\beta}\left({b}\:\mathrm{cos}\:\beta−{a}\:\mathrm{cos}\:\alpha−\mu{h}\right)={Mgb}\:\mathrm{cos}\:\beta−\left(\mathrm{2}{M}+{m}\right){ga}\:\mathrm{cos}\:\alpha \\ $$$$\frac{\mathrm{1}}{\mathrm{1}−\mu\:\mathrm{tan}\:\beta}\left({b}\:\mathrm{cos}\:\beta−{a}\:\mathrm{cos}\:\alpha−\mu{h}\right)={b}\:\mathrm{cos}\:\beta−\left(\mathrm{2}+\frac{{m}}{{M}}\right){a}\:\mathrm{cos}\:\alpha \\ $$$$\frac{{b}\:\mathrm{cos}\:\beta−\mu{h}}{\mathrm{1}−\mu\:\mathrm{tan}\:\beta}={b}\:\mathrm{cos}\:\beta−\left(\mathrm{2}+\frac{{m}}{{M}}−\frac{\mathrm{1}}{\mathrm{1}−\mu\:\mathrm{tan}\:\beta}\right){a}\:\mathrm{cos}\:\alpha \\ $$$$\Rightarrow\frac{\mu\left({h}−{b}\:\mathrm{sin}\:\beta\right)}{\mathrm{1}−\mu\:\mathrm{tan}\:\beta}=\left(\mathrm{2}+\frac{{m}}{{M}}−\frac{\mathrm{1}}{\mathrm{1}−\mu\:\mathrm{tan}\:\beta}\right)\sqrt{{a}^{\mathrm{2}} −\left({h}−{b}\:\mathrm{sin}\:\beta\right)^{\mathrm{2}} } \\ $$$$\Rightarrow\beta=…. \\ $$$$\Rightarrow{N}=\frac{{Mg}}{\mathrm{2}\left(\mathrm{1}−\mu\:\mathrm{tan}\:\beta\right)} \\ $$
Commented by ajfour last updated on 25/Jan/19
Very Nice Sir; thanks for attempting this way too.
$${Very}\:{Nice}\:{Sir};\:{thanks}\:{for}\:{attempting} \\ $$$${this}\:{way}\:{too}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *