Question Number 53843 by rahul 19 last updated on 26/Jan/19
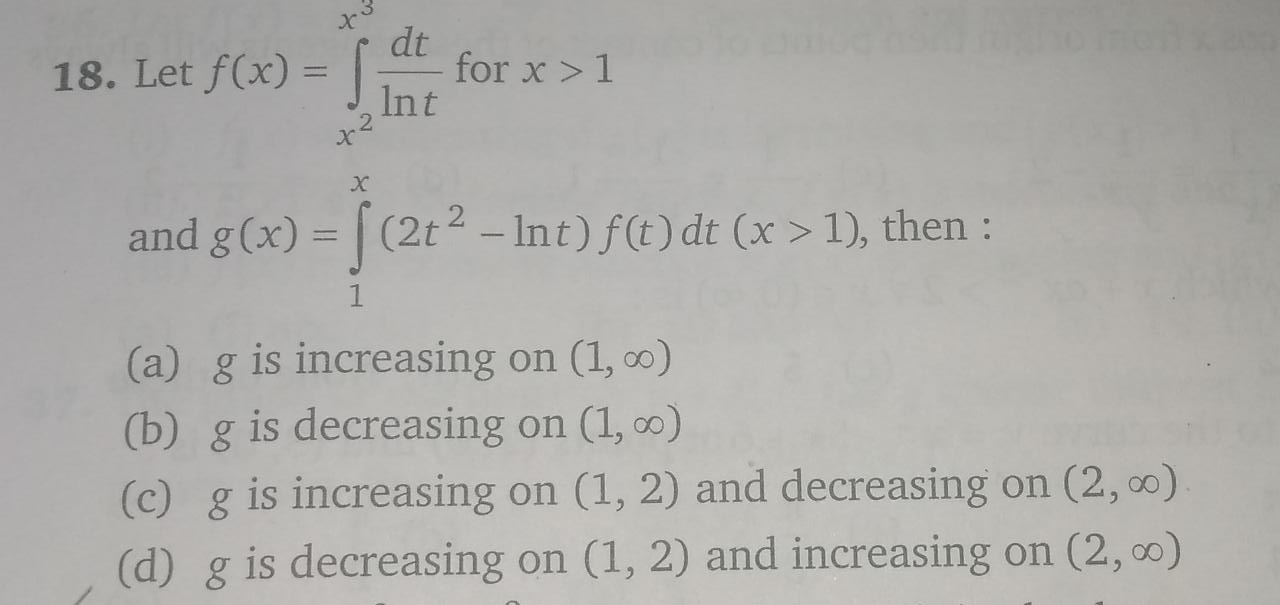
Answered by tanmay.chaudhury50@gmail.com last updated on 26/Jan/19
![(df/dx)=∫_x^2 ^x^3 (∂/∂x)((1/(lnt)))dt+(1/(lnx^3 ))((d(x^3 ))/dx)−(1/(lnx^2 ))((d(x^2 ))/dx) (df/dx)=0+((3x^2 )/(3lnx))−((2x)/(2lnx)) =((x(x−1))/(lnx)) (dg/dx)=∫_1 ^x (∂/∂x){(2t^2 −lnt)f(t)}dt+(2x^2 −lnx)f(x)(dx/dx)−{2×1^2 −ln1}f(1)((d(1))/dx) (dg/dx)=0+(2x^2 −lnx)f(x)−0 (dg/dx)=(2x^2 −lnx)f(x) f(x)=+ve [given x>1] (2x^2 −lnx)=+ve [given x>1] so g(x) increasing on (1,∞) pls check...](https://www.tinkutara.com/question/Q53850.png)
$$\frac{{df}}{{dx}}=\int_{{x}^{\mathrm{2}} } ^{{x}^{\mathrm{3}} } \:\frac{\partial}{\partial{x}}\left(\frac{\mathrm{1}}{{lnt}}\right){dt}+\frac{\mathrm{1}}{{lnx}^{\mathrm{3}} }\frac{{d}\left({x}^{\mathrm{3}} \right)}{{dx}}−\frac{\mathrm{1}}{{lnx}^{\mathrm{2}} }\frac{{d}\left({x}^{\mathrm{2}} \right)}{{dx}} \\ $$$$\frac{{df}}{{dx}}=\mathrm{0}+\frac{\mathrm{3}{x}^{\mathrm{2}} }{\mathrm{3}{lnx}}−\frac{\mathrm{2}{x}}{\mathrm{2}{lnx}} \\ $$$$\:=\frac{{x}\left({x}−\mathrm{1}\right)}{{lnx}} \\ $$$$\frac{{dg}}{{dx}}=\int_{\mathrm{1}} ^{{x}} \frac{\partial}{\partial{x}}\left\{\left(\mathrm{2}{t}^{\mathrm{2}} −{lnt}\right){f}\left({t}\right)\right\}{dt}+\left(\mathrm{2}{x}^{\mathrm{2}} −{lnx}\right){f}\left({x}\right)\frac{{dx}}{{dx}}−\left\{\mathrm{2}×\mathrm{1}^{\mathrm{2}} −{ln}\mathrm{1}\right\}{f}\left(\mathrm{1}\right)\frac{{d}\left(\mathrm{1}\right)}{{dx}} \\ $$$$\frac{{dg}}{{dx}}=\mathrm{0}+\left(\mathrm{2}{x}^{\mathrm{2}} −{lnx}\right){f}\left({x}\right)−\mathrm{0} \\ $$$$\frac{{dg}}{{dx}}=\left(\mathrm{2}{x}^{\mathrm{2}} −{lnx}\right){f}\left({x}\right) \\ $$$${f}\left({x}\right)=+{ve}\:\left[{given}\:{x}>\mathrm{1}\right] \\ $$$$\left(\mathrm{2}{x}^{\mathrm{2}} −{lnx}\right)=+{ve}\:\:\left[{given}\:{x}>\mathrm{1}\right] \\ $$$${so}\:{g}\left({x}\right)\:{increasing}\:{on}\:\left(\mathrm{1},\infty\right) \\ $$$${pls}\:{check}… \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by rahul 19 last updated on 26/Jan/19
thank you sir!
Commented by tanmay.chaudhury50@gmail.com last updated on 26/Jan/19

$${most}\:{welcome}… \\ $$
