Question Number 53962 by ajfour last updated on 27/Jan/19

Commented by ajfour last updated on 27/Jan/19

$${Find}\:{maximum}\:{perimeter}\:{of}\: \\ $$$${triangle}\:{APQ}.\left({have}\:{i}\:{posted}\:{this}\right. \\ $$$$\left.{question},\:{before},\:{i}'{m}\:{not}\:{sure}!?\right) \\ $$
Commented by ajfour last updated on 27/Jan/19
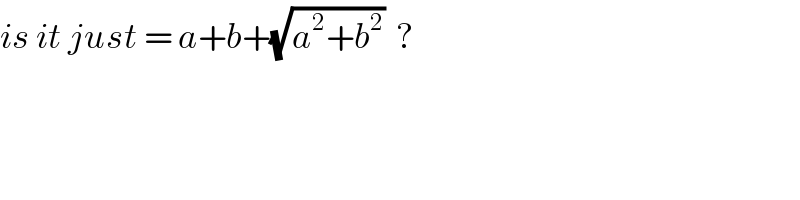
$${is}\:{it}\:{just}\:=\:{a}+{b}+\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\:\:? \\ $$
Commented by mr W last updated on 27/Jan/19

$${yes}\:{sir}. \\ $$
Answered by mr W last updated on 27/Jan/19

Commented by mr W last updated on 27/Jan/19
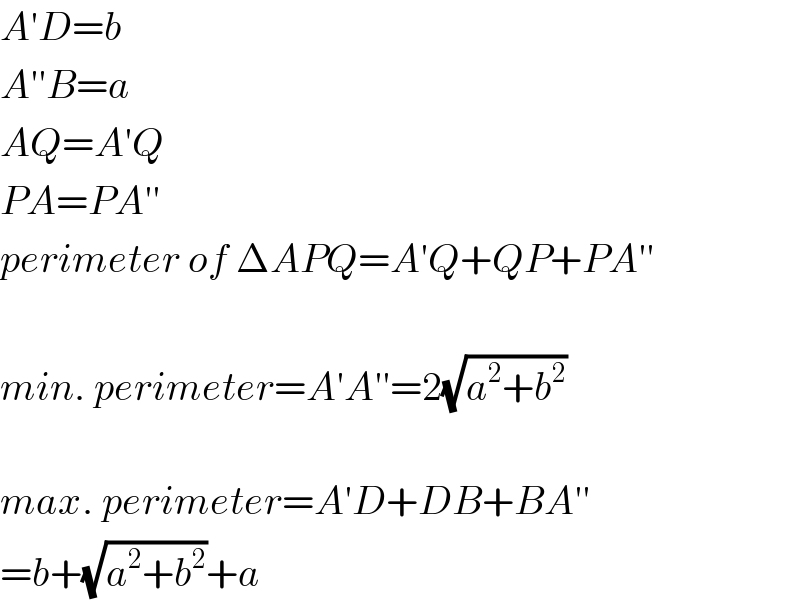
$${A}'{D}={b} \\ $$$${A}''{B}={a} \\ $$$${AQ}={A}'{Q} \\ $$$${PA}={PA}'' \\ $$$${perimeter}\:{of}\:\Delta{APQ}={A}'{Q}+{QP}+{PA}'' \\ $$$$ \\ $$$${min}.\:{perimeter}={A}'{A}''=\mathrm{2}\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$$ \\ $$$${max}.\:{perimeter}={A}'{D}+{DB}+{BA}'' \\ $$$$={b}+\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }+{a} \\ $$
Commented by ajfour last updated on 28/Jan/19

$${great}\:{technique}\:{to}\:{prove}\:{it}\:{Sir},\:{thank}\:{you}! \\ $$
