Question Number 54045 by ajfour last updated on 28/Jan/19

Commented by ajfour last updated on 28/Jan/19
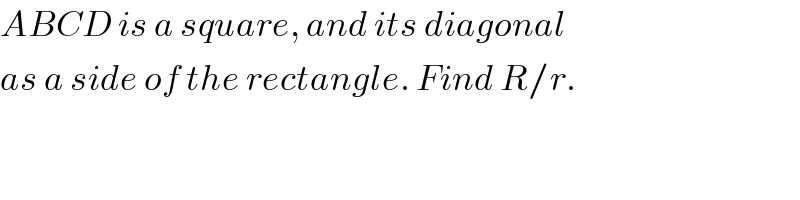
$${ABCD}\:{is}\:{a}\:{square},\:{and}\:{its}\:{diagonal} \\ $$$${as}\:{a}\:{side}\:{of}\:{the}\:{rectangle}.\:{Find}\:{R}/{r}. \\ $$
Answered by ajfour last updated on 28/Jan/19
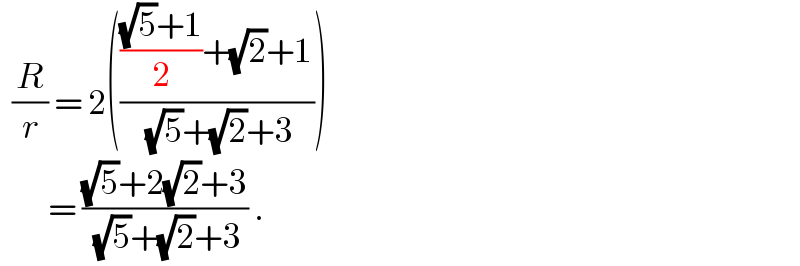
$$\:\:\frac{{R}}{{r}}\:=\:\mathrm{2}\left(\frac{\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{2}}+\sqrt{\mathrm{2}}+\mathrm{1}}{\:\sqrt{\mathrm{5}}+\sqrt{\mathrm{2}}+\mathrm{3}}\right)\: \\ $$$$\:\:\:\:\:\:\:\:=\:\frac{\sqrt{\mathrm{5}}+\mathrm{2}\sqrt{\mathrm{2}}+\mathrm{3}}{\:\sqrt{\mathrm{5}}+\sqrt{\mathrm{2}}+\mathrm{3}}\:. \\ $$
Answered by mr W last updated on 28/Jan/19
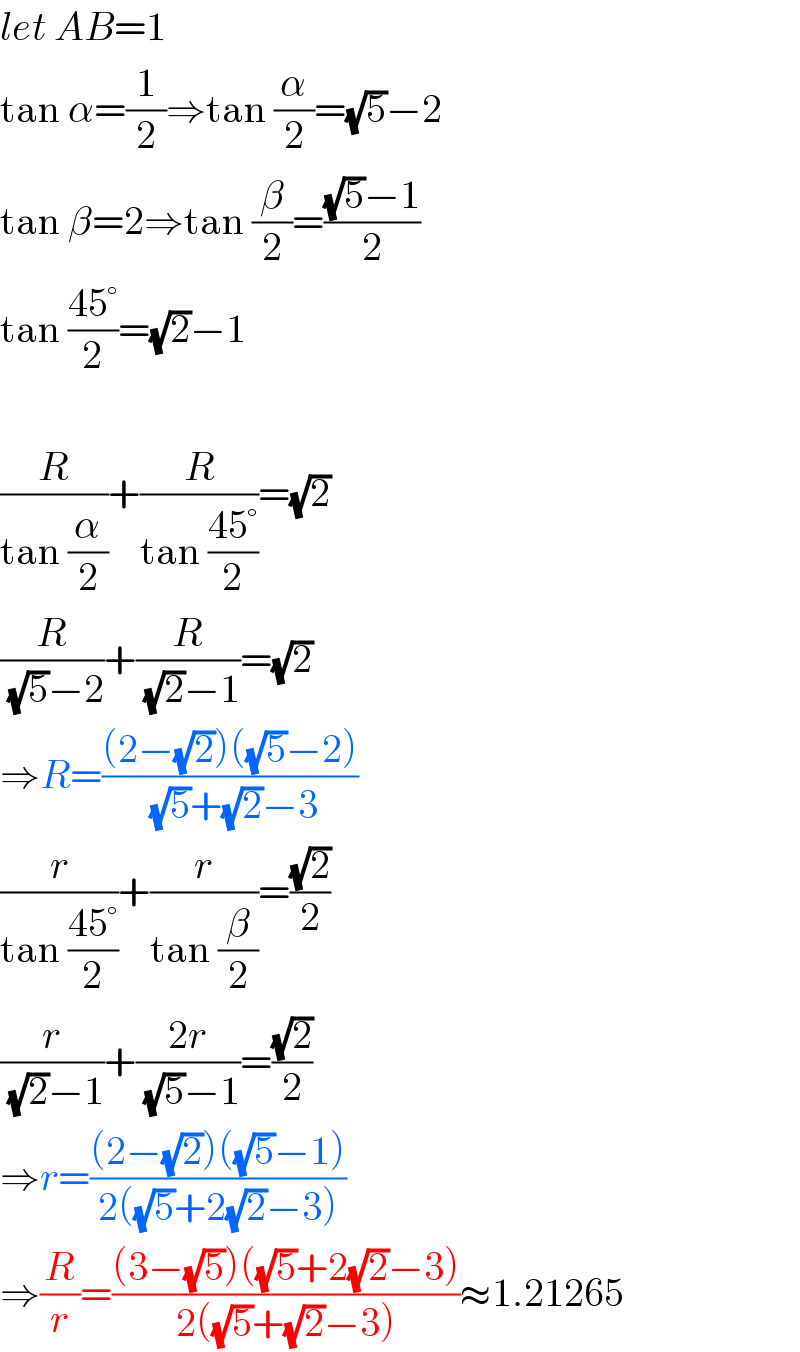
$${let}\:{AB}=\mathrm{1} \\ $$$$\mathrm{tan}\:\alpha=\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow\mathrm{tan}\:\frac{\alpha}{\mathrm{2}}=\sqrt{\mathrm{5}}−\mathrm{2} \\ $$$$\mathrm{tan}\:\beta=\mathrm{2}\Rightarrow\mathrm{tan}\:\frac{\beta}{\mathrm{2}}=\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{tan}\:\frac{\mathrm{45}°}{\mathrm{2}}=\sqrt{\mathrm{2}}−\mathrm{1} \\ $$$$ \\ $$$$\frac{{R}}{\mathrm{tan}\:\frac{\alpha}{\mathrm{2}}}+\frac{{R}}{\mathrm{tan}\:\frac{\mathrm{45}°}{\mathrm{2}}}=\sqrt{\mathrm{2}} \\ $$$$\frac{{R}}{\:\sqrt{\mathrm{5}}−\mathrm{2}}+\frac{{R}}{\:\sqrt{\mathrm{2}}−\mathrm{1}}=\sqrt{\mathrm{2}} \\ $$$$\Rightarrow{R}=\frac{\left(\mathrm{2}−\sqrt{\mathrm{2}}\right)\left(\sqrt{\mathrm{5}}−\mathrm{2}\right)}{\:\sqrt{\mathrm{5}}+\sqrt{\mathrm{2}}−\mathrm{3}} \\ $$$$\frac{{r}}{\mathrm{tan}\:\frac{\mathrm{45}°}{\mathrm{2}}}+\frac{{r}}{\mathrm{tan}\:\frac{\beta}{\mathrm{2}}}=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$$\frac{{r}}{\:\sqrt{\mathrm{2}}−\mathrm{1}}+\frac{\mathrm{2}{r}}{\:\sqrt{\mathrm{5}}−\mathrm{1}}=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$$\Rightarrow{r}=\frac{\left(\mathrm{2}−\sqrt{\mathrm{2}}\right)\left(\sqrt{\mathrm{5}}−\mathrm{1}\right)}{\mathrm{2}\left(\sqrt{\mathrm{5}}+\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{3}\right)} \\ $$$$\Rightarrow\frac{{R}}{{r}}=\frac{\left(\mathrm{3}−\sqrt{\mathrm{5}}\right)\left(\sqrt{\mathrm{5}}+\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{3}\right)}{\mathrm{2}\left(\sqrt{\mathrm{5}}+\sqrt{\mathrm{2}}−\mathrm{3}\right)}\approx\mathrm{1}.\mathrm{21265} \\ $$
Commented by ajfour last updated on 29/Jan/19

$${thanks}\:{Sir}.\: \\ $$
