Question Number 54061 by behi83417@gmail.com last updated on 28/Jan/19
Commented by mr W last updated on 29/Jan/19

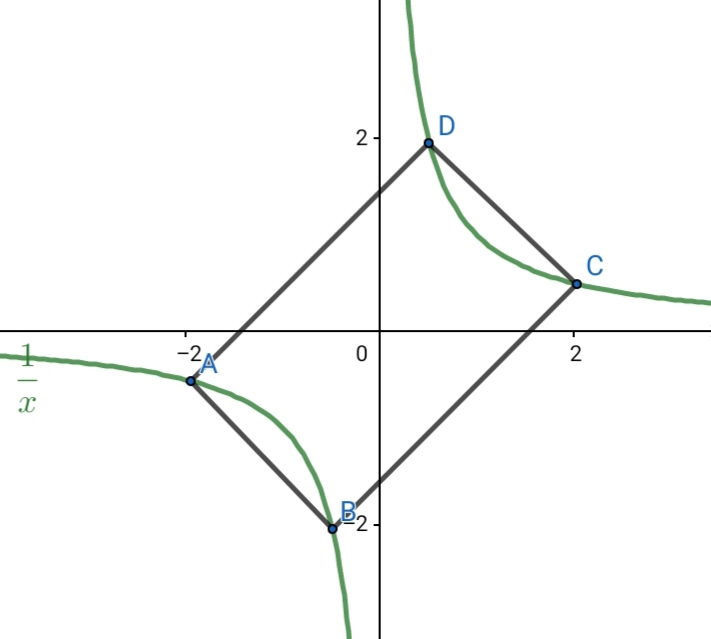
$${C}\left({t},\frac{\mathrm{1}}{{t}}\right) \\ $$$${D}\left(\frac{\mathrm{1}}{{t}},{t}\right) \\ $$$${CD}=\sqrt{\mathrm{2}}\left({t}−\frac{\mathrm{1}}{{t}}\right)=\mathrm{2} \\ $$$${t}^{\mathrm{2}} −\sqrt{\mathrm{2}}{t}−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{t}=\frac{\mathrm{1}+\sqrt{\mathrm{3}}}{\:\sqrt{\mathrm{2}}} \\ $$$${CB}=\sqrt{\mathrm{2}}\left(\frac{\mathrm{1}+\sqrt{\mathrm{3}}}{\:\sqrt{\mathrm{2}}}+\frac{\sqrt{\mathrm{2}}}{\mathrm{1}+\sqrt{\mathrm{3}}}\right)=\mathrm{2}\sqrt{\mathrm{3}} \\ $$$${Area}\:{of}\:{rectangle}=\mathrm{2}×\mathrm{2}\sqrt{\mathrm{3}}=\mathrm{4}\sqrt{\mathrm{3}} \\ $$$$ \\ $$$${there}\:{is}\:{only}\:{one}\:{possible}\:{rectangle}. \\ $$$${but}\:{question}\:{asks}\:{for}\:{maximum}\:\:{rectangle}. \\ $$
Commented by behi83417@gmail.com last updated on 28/Jan/19

$${ABCD},{is}\:{a}\:{rectangle}\:{and}\:{its}\:{diagonals} \\ $$$${meet}\:{each}\:{other}\:{at}\:{center}\:{point}\:{of}: \\ $$$$\boldsymbol{{xy}}−{plane}. \\ $$$${if}:{AB}=\mathrm{2}\:\left({constant}\right),{find}\:{maximum} \\ $$$${area}\:{of}\:{rectangle}. \\ $$
Commented by behi83417@gmail.com last updated on 28/Jan/19

$$? \\ $$
Commented by behi83417@gmail.com last updated on 28/Jan/19
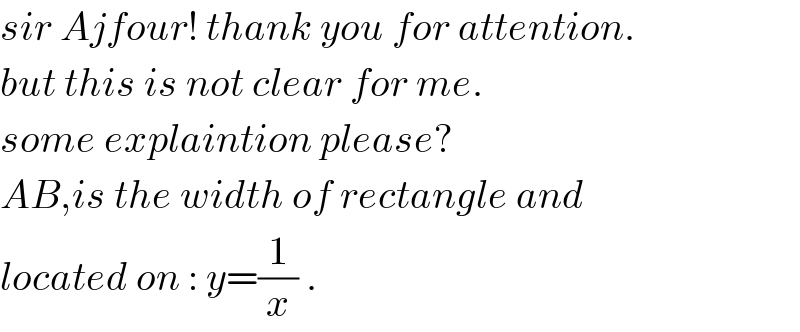
$${sir}\:{Ajfour}!\:{thank}\:{you}\:{for}\:{attention}. \\ $$$${but}\:{this}\:{is}\:{not}\:{clear}\:{for}\:{me}. \\ $$$${some}\:{explaintion}\:{please}? \\ $$$${AB},{is}\:{the}\:{width}\:{of}\:{rectangle}\:{and} \\ $$$${located}\:{on}\::\:{y}=\frac{\mathrm{1}}{{x}}\:. \\ $$
Commented by behi83417@gmail.com last updated on 29/Jan/19
$${thanks}\:{in}\:{advance}\:{dear}\:{master}. \\ $$$${what}\:{about}\:{answer}\:{if}\::{ABCD}\:{be}\:{a} \\ $$$${parallelogram}? \\ $$
Commented by behi83417@gmail.com last updated on 29/Jan/19

$${I}\:{don}'{t}\:{recive}\:{any}\:{notifications}\:{from} \\ $$$${tinkutara}\:{app}.{am}\:{i}\:{alone}? \\ $$
Commented by mr W last updated on 29/Jan/19

$${i}\:{don}'{t}\:{get}\:{notifications}\:{either}.\:{so}\:{i} \\ $$$${don}'{t}\:{know}\:{if}\:{someone}\:{has}\:{commented} \\ $$$${my}\:{posts}. \\ $$
Commented by peter frank last updated on 30/Jan/19
$${true}\:{the}\:{same}\:{to}\:\:{me}\:{i}\:{dont}\:{get}\:{notification}. \\ $$
