Question Number 54068 by ajfour last updated on 28/Jan/19

Commented by ajfour last updated on 28/Jan/19

$${locate}\:{P}\:\left({x},{y}\right)\:{such}\:{that}\:\bigtriangleup{APB}, \\ $$$$\bigtriangleup{BPC},\:{and}\:\bigtriangleup{CPA}\:{each}\:{have}\:{the} \\ $$$${same}\:{perimeter}.\:\left({in}\:{terms}\:{of}\:{a},{b},{c}\right) \\ $$
Commented by mr W last updated on 28/Jan/19
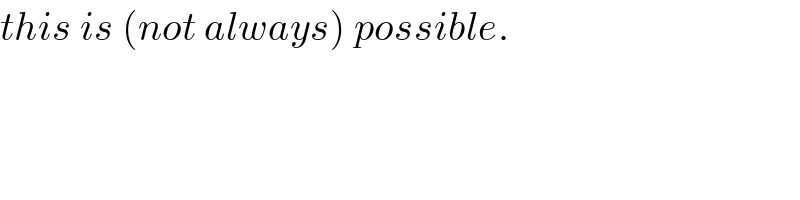
$${this}\:{is}\:\left({not}\:{always}\right)\:{possible}. \\ $$
Answered by mr W last updated on 28/Jan/19

$${s}=\sqrt{\left({x}−{x}_{{A}} \right)^{\mathrm{2}} +\left({y}−{y}_{{A}} \right)^{\mathrm{2}} }+\sqrt{\left({x}−{x}_{{B}} \right)^{\mathrm{2}} +\left({y}−{y}_{{B}} \right)^{\mathrm{2}} }+\sqrt{\left({x}_{{A}} −{x}_{{B}} \right)^{\mathrm{2}} +\left({y}_{{A}} −{y}_{{B}} \right)^{\mathrm{2}} } \\ $$$${s}=\sqrt{\left({x}−{x}_{{B}} \right)^{\mathrm{2}} +\left({y}−{y}_{{B}} \right)^{\mathrm{2}} }+\sqrt{\left({x}−{x}_{{C}} \right)^{\mathrm{2}} +\left({y}−{y}_{{C}} \right)^{\mathrm{2}} }+\sqrt{\left({x}_{{B}} −{x}_{{C}} \right)^{\mathrm{2}} +\left({y}_{{B}} −{y}_{{C}} \right)^{\mathrm{2}} } \\ $$$${s}=\sqrt{\left({x}−{x}_{{C}} \right)^{\mathrm{2}} +\left({y}−{y}_{{C}} \right)^{\mathrm{2}} }+\sqrt{\left({x}−{x}_{{A}} \right)^{\mathrm{2}} +\left({y}−{y}_{{A}} \right)^{\mathrm{2}} }+\sqrt{\left({x}_{{C}} −{x}_{{A}} \right)^{\mathrm{2}} +\left({y}_{{C}} −{y}_{{A}} \right)^{\mathrm{2}} } \\ $$$$\mathrm{3}\:{eqn}.\:{with}\:\mathrm{3}\:{unknowns}\:{x},{y},{s}. \\ $$$${A}\left(\mathrm{0},\mathrm{0}\right) \\ $$$${B}\left({b},\mathrm{0}\right) \\ $$$${C}\left({c},{d}\right) \\ $$$${s}=\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }+\sqrt{\left({x}−{b}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} }+{b} \\ $$$${s}=\sqrt{\left({x}−{b}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} }+\sqrt{\left({x}−{c}\right)^{\mathrm{2}} +\left({y}−{d}\right)^{\mathrm{2}} }+\sqrt{\left({b}−{c}\right)^{\mathrm{2}} +{d}^{\mathrm{2}} } \\ $$$${s}=\sqrt{\left({x}−{c}\right)^{\mathrm{2}} +\left({y}−{d}\right)^{\mathrm{2}} }+\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }+\sqrt{{c}^{\mathrm{2}} +{d}^{\mathrm{2}} } \\ $$$$ \\ $$$$\Rightarrow\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }−\sqrt{\left({x}−{c}\right)^{\mathrm{2}} +\left({y}−{d}\right)^{\mathrm{2}} }=\sqrt{\left({b}−{c}\right)^{\mathrm{2}} +{d}^{\mathrm{2}} }−{b} \\ $$$$\Rightarrow\sqrt{\left({x}−{b}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} }−\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }=\sqrt{{c}^{\mathrm{2}} +{d}^{\mathrm{2}} }−\sqrt{\left({b}−{c}\right)^{\mathrm{2}} +{d}^{\mathrm{2}} } \\ $$$$ \\ $$$${example}: \\ $$$${A}\left(\mathrm{0},\mathrm{0}\right),\:{B}\left(\mathrm{5},\mathrm{0}\right),\:{C}\left(\mathrm{2},\mathrm{4}\right) \\ $$$$\Rightarrow{P}\left(\mathrm{2}.\mathrm{7888},\mathrm{1}.\mathrm{1056}\right) \\ $$
Commented by mr W last updated on 28/Jan/19

$${that}\:{was}\:{an}\:{error}. \\ $$
Commented by ajfour last updated on 28/Jan/19

$${Thank}\:{you}\:{Sir}\:. \\ $$
Commented by ajfour last updated on 28/Jan/19
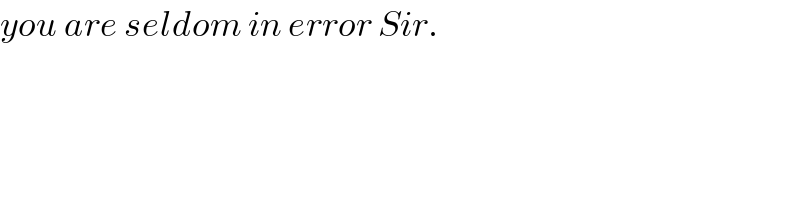
$${you}\:{are}\:{seldom}\:{in}\:{error}\:{Sir}. \\ $$
