Menu Close

Question-54160

Tinku Tara 0 Comments
Pin




Question Number 54160 by ajfour last updated on 30/Jan/19
Commented by ajfour last updated on 30/Jan/19
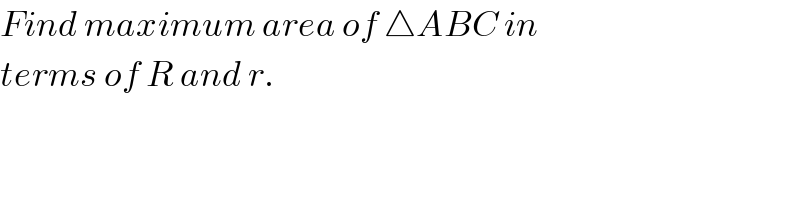
Find maximum area of △ABC in terms of R and r.
$${Find}\:{maximum}\:{area}\:{of}\:\bigtriangleup{ABC}\:{in} \\ $$$${terms}\:{of}\:{R}\:{and}\:{r}. \\ $$
Answered by mr W last updated on 30/Jan/19
Commented by mr W last updated on 30/Jan/19
α=(π/2)−(β/2) ⇒2α=π−β ..(i) β=(π/2)−(α/2) ⇒2β=π−α ..(ii) ⇒α=β=(π/3)=60° AC=2R cos (α/2)=(√3)R AB=2r cos (β/2)=(√3)r ∠CAB=180°−(α/2)−(β/2)=120° Δ_(max) =(1/2)×(√3)R×(√3)r×sin 120° ⇒Δ_(max) =((3(√3)Rr)/4)
$$\alpha=\frac{\pi}{\mathrm{2}}−\frac{\beta}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{2}\alpha=\pi−\beta\:\:\:..\left({i}\right) \\ $$$$\beta=\frac{\pi}{\mathrm{2}}−\frac{\alpha}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{2}\beta=\pi−\alpha\:\:..\left({ii}\right) \\ $$$$\Rightarrow\alpha=\beta=\frac{\pi}{\mathrm{3}}=\mathrm{60}° \\ $$$${AC}=\mathrm{2}{R}\:\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}=\sqrt{\mathrm{3}}{R} \\ $$$${AB}=\mathrm{2}{r}\:\mathrm{cos}\:\frac{\beta}{\mathrm{2}}=\sqrt{\mathrm{3}}{r} \\ $$$$\angle{CAB}=\mathrm{180}°−\frac{\alpha}{\mathrm{2}}−\frac{\beta}{\mathrm{2}}=\mathrm{120}° \\ $$$$\Delta_{{max}} =\frac{\mathrm{1}}{\mathrm{2}}×\sqrt{\mathrm{3}}{R}×\sqrt{\mathrm{3}}{r}×\mathrm{sin}\:\mathrm{120}° \\ $$$$\Rightarrow\Delta_{{max}} =\frac{\mathrm{3}\sqrt{\mathrm{3}}{Rr}}{\mathrm{4}} \\ $$
Commented by ajfour last updated on 30/Jan/19
yes Sir, straight and clear, thanks again(i am quite dumb at this).
$${yes}\:{Sir},\:{straight}\:{and}\:{clear},\:{thanks} \\ $$$${again}\left({i}\:{am}\:{quite}\:{dumb}\:{at}\:{this}\right). \\ $$
Commented by mr W last updated on 30/Jan/19
i tried above to find the maximum triangle only using logic. but we can get the same result using calculus: Δ=(1/2)×2R cos (α/2)×2r cos (β/2)×sin ((α/2)+(β/2)) =2Rr cos (α/2) cos (β/2) sin ((α/2)+(β/2)) ((∂(Δ))/∂α)=2Rrcos (β/2){−(1/2)sin (α/2) sin ((α/2)+(β/2))+(1/2)cos (α/2) cos ((α/2)+(β/2))}=0 sin (α/2) sin ((α/2)+(β/2))=cos (α/2) cos ((α/2)+(β/2)) ⇒tan (α/2) tan ((α/2)+(β/2))=1 ...(i) ((∂(Δ))/∂β)=2Rrcos (α/2){−(1/2)sin (β/2) sin ((α/2)+(β/2))+(1/2)cos (β/2) cos ((α/2)+(β/2))}=0 ⇒tan (β/2) tan ((α/2)+(β/2))=1 ...(ii) ⇒tan (α/2)=tan (β/2) ⇒α=β ⇒tan (α/2) tan α=1 ⇒tan (α/2) ((2 tan (α/2))/(1−tan^2 (α/2)))=1 ⇒3 tan^2 (α/2)=1 ⇒tan (α/2)=(1/( (√3))) ⇒(α/2)=30° ⇒α=β=60°
$${i}\:{tried}\:{above}\:{to}\:{find}\:{the}\:{maximum}\:{triangle} \\ $$$${only}\:{using}\:{logic}.\:{but}\:{we}\:{can}\:{get}\:{the} \\ $$$${same}\:{result}\:{using}\:{calculus}: \\ $$$$\Delta=\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{2}{R}\:\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}×\mathrm{2}{r}\:\mathrm{cos}\:\frac{\beta}{\mathrm{2}}×\mathrm{sin}\:\left(\frac{\alpha}{\mathrm{2}}+\frac{\beta}{\mathrm{2}}\right) \\ $$$$=\mathrm{2}{Rr}\:\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}\:\mathrm{cos}\:\frac{\beta}{\mathrm{2}}\:\mathrm{sin}\:\left(\frac{\alpha}{\mathrm{2}}+\frac{\beta}{\mathrm{2}}\right) \\ $$$$\frac{\partial\left(\Delta\right)}{\partial\alpha}=\mathrm{2}{Rr}\mathrm{cos}\:\frac{\beta}{\mathrm{2}}\left\{−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\frac{\alpha}{\mathrm{2}}\:\mathrm{sin}\:\left(\frac{\alpha}{\mathrm{2}}+\frac{\beta}{\mathrm{2}}\right)+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}\:\mathrm{cos}\:\left(\frac{\alpha}{\mathrm{2}}+\frac{\beta}{\mathrm{2}}\right)\right\}=\mathrm{0} \\ $$$$\mathrm{sin}\:\frac{\alpha}{\mathrm{2}}\:\mathrm{sin}\:\left(\frac{\alpha}{\mathrm{2}}+\frac{\beta}{\mathrm{2}}\right)=\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}\:\mathrm{cos}\:\left(\frac{\alpha}{\mathrm{2}}+\frac{\beta}{\mathrm{2}}\right) \\ $$$$\Rightarrow\mathrm{tan}\:\frac{\alpha}{\mathrm{2}}\:\mathrm{tan}\:\left(\frac{\alpha}{\mathrm{2}}+\frac{\beta}{\mathrm{2}}\right)=\mathrm{1}\:\:\:…\left({i}\right) \\ $$$$\frac{\partial\left(\Delta\right)}{\partial\beta}=\mathrm{2}{Rr}\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}\left\{−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\frac{\beta}{\mathrm{2}}\:\mathrm{sin}\:\left(\frac{\alpha}{\mathrm{2}}+\frac{\beta}{\mathrm{2}}\right)+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:\frac{\beta}{\mathrm{2}}\:\mathrm{cos}\:\left(\frac{\alpha}{\mathrm{2}}+\frac{\beta}{\mathrm{2}}\right)\right\}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{tan}\:\frac{\beta}{\mathrm{2}}\:\mathrm{tan}\:\left(\frac{\alpha}{\mathrm{2}}+\frac{\beta}{\mathrm{2}}\right)=\mathrm{1}\:\:\:…\left({ii}\right) \\ $$$$\Rightarrow\mathrm{tan}\:\frac{\alpha}{\mathrm{2}}=\mathrm{tan}\:\frac{\beta}{\mathrm{2}} \\ $$$$\Rightarrow\alpha=\beta \\ $$$$\Rightarrow\mathrm{tan}\:\frac{\alpha}{\mathrm{2}}\:\mathrm{tan}\:\alpha=\mathrm{1} \\ $$$$\Rightarrow\mathrm{tan}\:\frac{\alpha}{\mathrm{2}}\:\frac{\mathrm{2}\:\mathrm{tan}\:\frac{\alpha}{\mathrm{2}}}{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:\frac{\alpha}{\mathrm{2}}}=\mathrm{1} \\ $$$$\Rightarrow\mathrm{3}\:\mathrm{tan}^{\mathrm{2}} \:\frac{\alpha}{\mathrm{2}}=\mathrm{1} \\ $$$$\Rightarrow\mathrm{tan}\:\frac{\alpha}{\mathrm{2}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}} \\ $$$$\Rightarrow\frac{\alpha}{\mathrm{2}}=\mathrm{30}° \\ $$$$\Rightarrow\alpha=\beta=\mathrm{60}° \\ $$
Commented by ajfour last updated on 30/Jan/19
using calculus i′d got the same, but would you please explain your logic to me in some more detail, Sir?
$${using}\:{calculus}\:{i}'{d}\:{got}\:{the}\:{same}, \\ $$$${but}\:{would}\:{you}\:{please}\:{explain}\:{your} \\ $$$${logic}\:{to}\:{me}\:{in}\:{some}\:{more}\:{detail},\:{Sir}? \\ $$
Commented by mr W last updated on 30/Jan/19
the logic is: with maximum triangle tangent at C is parallel to AB, i.e. CP⊥AB. tangent at B is parallel to AC, i.e. BQ⊥AC.
$${the}\:{logic}\:{is}: \\ $$$${with}\:{maximum}\:{triangle} \\ $$$${tangent}\:{at}\:{C}\:{is}\:{parallel}\:{to}\:{AB},\:{i}.{e}. \\ $$$${CP}\bot{AB}. \\ $$$${tangent}\:{at}\:{B}\:{is}\:{parallel}\:{to}\:{AC},\:{i}.{e}. \\ $$$${BQ}\bot{AC}. \\ $$
Commented by mr W last updated on 30/Jan/19
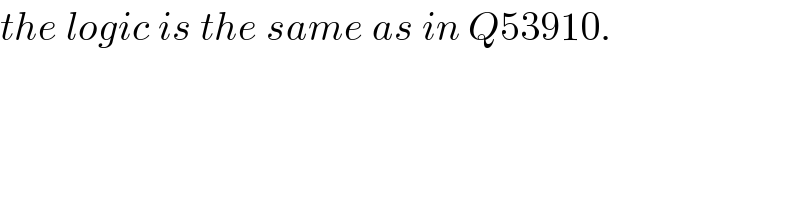
the logic is the same as in Q53910.
$${the}\:{logic}\:{is}\:{the}\:{same}\:{as}\:{in}\:{Q}\mathrm{53910}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *