Menu Close

Question-54194

Tinku Tara 0 Comments
Pin




Question Number 54194 by ajfour last updated on 30/Jan/19
Commented by ajfour last updated on 31/Jan/19
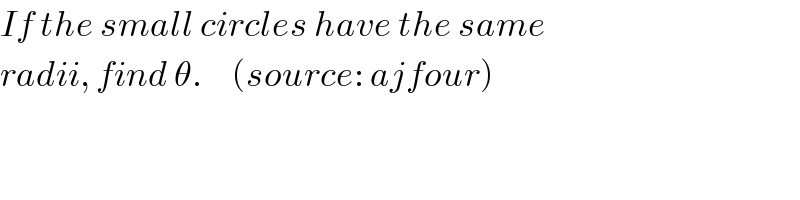
If the small circles have the same radii, find θ. (source: ajfour)
$${If}\:{the}\:{small}\:{circles}\:{have}\:{the}\:{same} \\ $$$${radii},\:{find}\:\theta.\:\:\:\:\:\left({source}:\:{ajfour}\right) \\ $$
Answered by ajfour last updated on 30/Jan/19
Commented by mr W last updated on 31/Jan/19
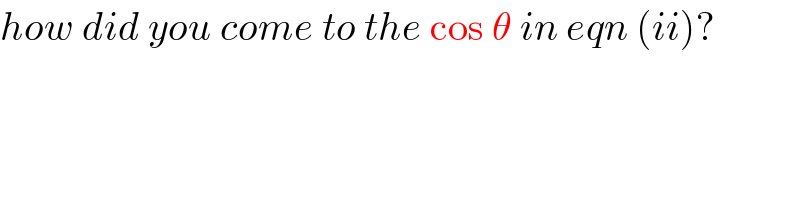
how did you come to the cos θ in eqn (ii)?
$${how}\:{did}\:{you}\:{come}\:{to}\:{the}\:\mathrm{cos}\:\theta\:{in}\:{eqn}\:\left({ii}\right)?\: \\ $$
Commented by ajfour last updated on 31/Jan/19
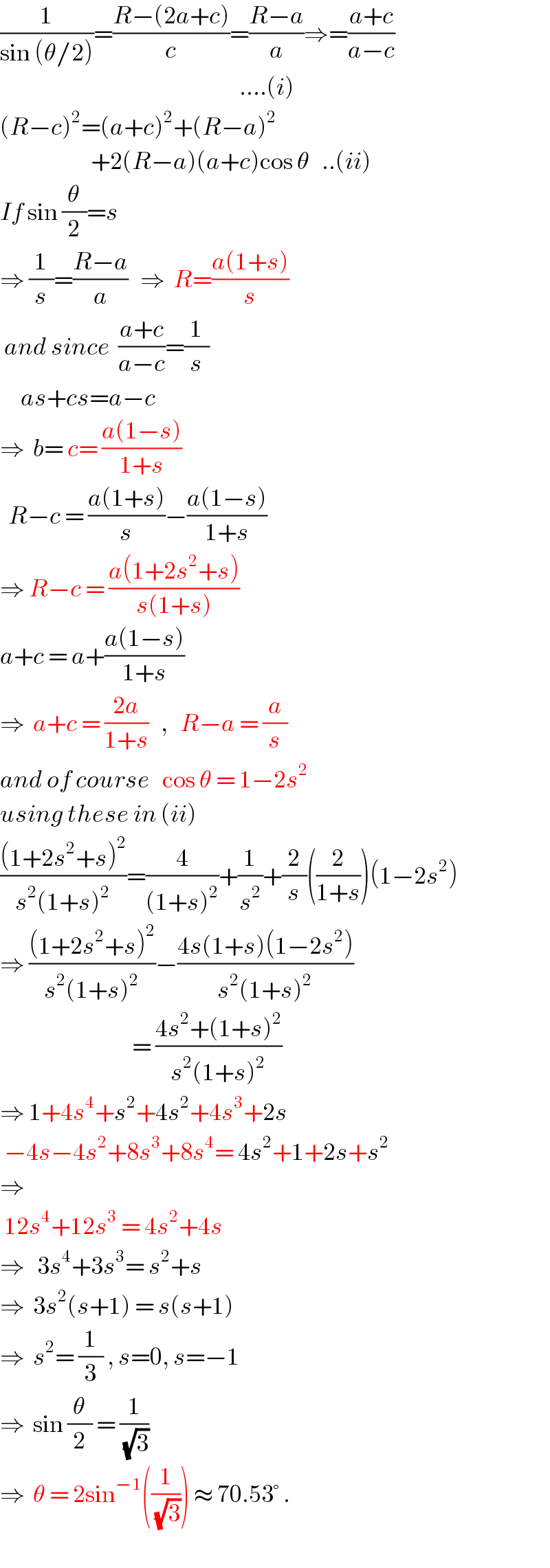
(1/(sin (θ/2)))=((R−(2a+c))/c)=((R−a)/a)⇒=((a+c)/(a−c)) ....(i) (R−c)^2 =(a+c)^2 +(R−a)^2 +2(R−a)(a+c)cos θ ..(ii) If sin (θ/2)=s ⇒ (1/s)=((R−a)/a) ⇒ R=((a(1+s))/s) and since ((a+c)/(a−c))=(1/s) as+cs=a−c ⇒ b= c= ((a(1−s))/(1+s)) R−c = ((a(1+s))/s)−((a(1−s))/(1+s)) ⇒ R−c = ((a(1+2s^2 +s))/(s(1+s))) a+c = a+((a(1−s))/(1+s)) ⇒ a+c = ((2a)/(1+s)) , R−a = (a/s) and of course cos θ = 1−2s^2 using these in (ii) (((1+2s^2 +s)^2 )/(s^2 (1+s)^2 ))=(4/((1+s)^2 ))+(1/s^2 )+(2/s)((2/(1+s)))(1−2s^2 ) ⇒ (((1+2s^2 +s)^2 )/(s^2 (1+s)^2 ))−((4s(1+s)(1−2s^2 ))/(s^2 (1+s)^2 )) = ((4s^2 +(1+s)^2 )/(s^2 (1+s)^2 )) ⇒ 1+4s^4 +s^2 +4s^2 +4s^3 +2s −4s−4s^2 +8s^3 +8s^4 = 4s^2 +1+2s+s^2 ⇒ 12s^4 +12s^3 = 4s^2 +4s ⇒ 3s^4 +3s^3 = s^2 +s ⇒ 3s^2 (s+1) = s(s+1) ⇒ s^2 = (1/3) , s=0, s=−1 ⇒ sin (θ/2) = (1/( (√3))) ⇒ θ = 2sin^(−1) ((1/( (√3)))) ≈ 70.53° .
$$\frac{\mathrm{1}}{\mathrm{sin}\:\left(\theta/\mathrm{2}\right)}=\frac{{R}−\left(\mathrm{2}{a}+{c}\right)}{{c}}=\frac{{R}−{a}}{{a}}\Rightarrow=\frac{{a}+{c}}{{a}−{c}}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:….\left({i}\right) \\ $$$$\left({R}−{c}\right)^{\mathrm{2}} =\left({a}+{c}\right)^{\mathrm{2}} +\left({R}−{a}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{2}\left({R}−{a}\right)\left({a}+{c}\right)\mathrm{cos}\:\theta\:\:\:..\left({ii}\right) \\ $$$${If}\:\mathrm{sin}\:\frac{\theta}{\mathrm{2}}={s} \\ $$$$\Rightarrow\:\frac{\mathrm{1}}{{s}}=\frac{{R}−{a}}{{a}}\:\:\:\Rightarrow\:\:{R}=\frac{{a}\left(\mathrm{1}+{s}\right)}{{s}} \\ $$$$\:{and}\:{since}\:\:\frac{{a}+{c}}{{a}−{c}}=\frac{\mathrm{1}}{{s}} \\ $$$$\:\:\:\:\:{as}+{cs}={a}−{c} \\ $$$$\Rightarrow\:\:{b}=\:{c}=\:\frac{{a}\left(\mathrm{1}−{s}\right)}{\mathrm{1}+{s}} \\ $$$$\:\:{R}−{c}\:=\:\frac{{a}\left(\mathrm{1}+{s}\right)}{{s}}−\frac{{a}\left(\mathrm{1}−{s}\right)}{\mathrm{1}+{s}} \\ $$$$\Rightarrow\:{R}−{c}\:=\:\frac{{a}\left(\mathrm{1}+\mathrm{2}{s}^{\mathrm{2}} +{s}\right)}{{s}\left(\mathrm{1}+{s}\right)} \\ $$$${a}+{c}\:=\:{a}+\frac{{a}\left(\mathrm{1}−{s}\right)}{\mathrm{1}+{s}} \\ $$$$\Rightarrow\:\:{a}+{c}\:=\:\frac{\mathrm{2}{a}}{\mathrm{1}+{s}}\:\:\:,\:\:\:{R}−{a}\:=\:\frac{{a}}{{s}} \\ $$$${and}\:{of}\:{course}\:\:\:\mathrm{cos}\:\theta\:=\:\mathrm{1}−\mathrm{2}{s}^{\mathrm{2}} \\ $$$${using}\:{these}\:{in}\:\left({ii}\right) \\ $$$$\frac{\left(\mathrm{1}+\mathrm{2}{s}^{\mathrm{2}} +{s}\right)^{\mathrm{2}} }{{s}^{\mathrm{2}} \left(\mathrm{1}+{s}\right)^{\mathrm{2}} }=\frac{\mathrm{4}}{\left(\mathrm{1}+{s}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{{s}^{\mathrm{2}} }+\frac{\mathrm{2}}{{s}}\left(\frac{\mathrm{2}}{\mathrm{1}+{s}}\right)\left(\mathrm{1}−\mathrm{2}{s}^{\mathrm{2}} \right) \\ $$$$\Rightarrow\:\frac{\left(\mathrm{1}+\mathrm{2}{s}^{\mathrm{2}} +{s}\right)^{\mathrm{2}} }{{s}^{\mathrm{2}} \left(\mathrm{1}+{s}\right)^{\mathrm{2}} }−\frac{\mathrm{4}{s}\left(\mathrm{1}+{s}\right)\left(\mathrm{1}−\mathrm{2}{s}^{\mathrm{2}} \right)}{{s}^{\mathrm{2}} \left(\mathrm{1}+{s}\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{4}{s}^{\mathrm{2}} +\left(\mathrm{1}+{s}\right)^{\mathrm{2}} }{{s}^{\mathrm{2}} \left(\mathrm{1}+{s}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow\:\mathrm{1}+\mathrm{4}{s}^{\mathrm{4}} +{s}^{\mathrm{2}} +\mathrm{4}{s}^{\mathrm{2}} +\mathrm{4}{s}^{\mathrm{3}} +\mathrm{2}{s} \\ $$$$\:−\mathrm{4}{s}−\mathrm{4}{s}^{\mathrm{2}} +\mathrm{8}{s}^{\mathrm{3}} +\mathrm{8}{s}^{\mathrm{4}} =\:\mathrm{4}{s}^{\mathrm{2}} +\mathrm{1}+\mathrm{2}{s}+{s}^{\mathrm{2}} \\ $$$$\Rightarrow \\ $$$$\:\mathrm{12}{s}^{\mathrm{4}} +\mathrm{12}{s}^{\mathrm{3}} \:=\:\mathrm{4}{s}^{\mathrm{2}} +\mathrm{4}{s} \\ $$$$\Rightarrow\:\:\:\mathrm{3}{s}^{\mathrm{4}} +\mathrm{3}{s}^{\mathrm{3}} =\:{s}^{\mathrm{2}} +{s} \\ $$$$\Rightarrow\:\:\mathrm{3}{s}^{\mathrm{2}} \left({s}+\mathrm{1}\right)\:=\:{s}\left({s}+\mathrm{1}\right) \\ $$$$\Rightarrow\:\:{s}^{\mathrm{2}} =\:\frac{\mathrm{1}}{\mathrm{3}}\:,\:{s}=\mathrm{0},\:{s}=−\mathrm{1} \\ $$$$\Rightarrow\:\:\mathrm{sin}\:\frac{\theta}{\mathrm{2}}\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\: \\ $$$$\Rightarrow\:\:\theta\:=\:\mathrm{2sin}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\:\approx\:\mathrm{70}.\mathrm{53}°\:. \\ $$
Commented by ajfour last updated on 31/Jan/19
Commented by ajfour last updated on 31/Jan/19
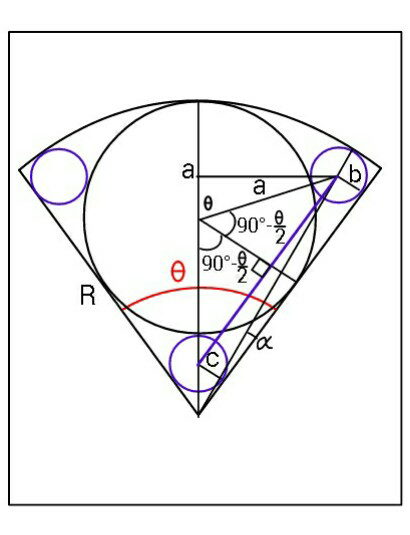
(R−b)^2 =(a+b)^2 sin^2 θ+ [(R−a)+(a+b)cos θ]^2 ⇒(R−b)^2 =(a+b)^2 +2(R−a)(a+b)cos θ and b=c ⇒(R−c)^2 =(a+c)^2 +2(R−a)(a+c)cos θ will that do Sir ?
$$\left({R}−{b}\right)^{\mathrm{2}} =\left({a}+{b}\right)^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta+ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left[\left({R}−{a}\right)+\left({a}+{b}\right)\mathrm{cos}\:\theta\right]^{\mathrm{2}} \\ $$$$\Rightarrow\left({R}−{b}\right)^{\mathrm{2}} =\left({a}+{b}\right)^{\mathrm{2}} +\mathrm{2}\left({R}−{a}\right)\left({a}+{b}\right)\mathrm{cos}\:\theta \\ $$$${and}\:{b}={c}\: \\ $$$$\Rightarrow\left({R}−{c}\right)^{\mathrm{2}} =\left({a}+{c}\right)^{\mathrm{2}} +\mathrm{2}\left({R}−{a}\right)\left({a}+{c}\right)\mathrm{cos}\:\theta \\ $$$${will}\:{that}\:{do}\:{Sir}\:? \\ $$
Commented by mr W last updated on 31/Jan/19
thanks sir!
$${thanks}\:{sir}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *