Question Number 54206 by ajfour last updated on 31/Jan/19
Commented by ajfour last updated on 31/Jan/19

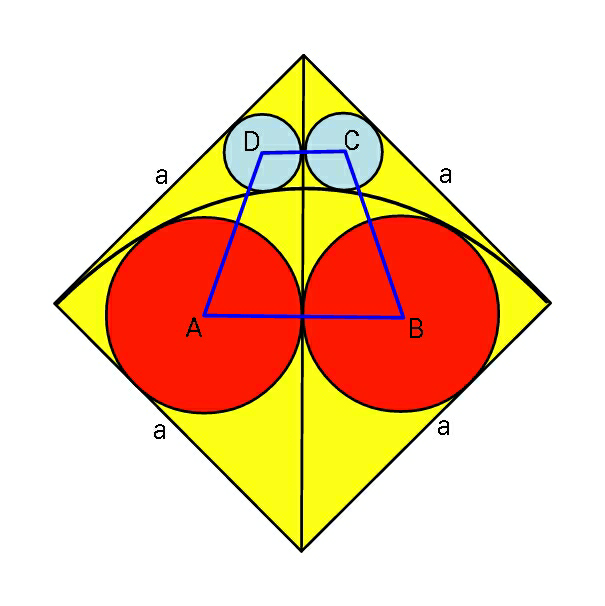
$${Find}\:{the}\:{area}\:{of}\:{trapezium}\:{ABCD} \\ $$$${in}\:{terms}\:{of}\:\boldsymbol{{a}}.\:\left({the}\:{red}\:{circles}\:{are}\:{each}\right. \\ $$$${within}\:{a}\:{half}\:{quarter}\:{circle}\:{and}\:{the} \\ $$$$\left.{outer}\:{boundary}\:{is}\:{a}\:{square}\:{of}\:{side}\:\boldsymbol{{a}}\right). \\ $$
Commented by ajfour last updated on 31/Jan/19
$$\left({like}\:{children},\:{we}\:{should}\:{still}\:{play}\:!\right) \\ $$
Answered by mr W last updated on 31/Jan/19
![(c/(tan ((45°)/2)))+(√((a+c)^2 −c^2 ))=(√2)a ⇒((√2)+1)c+(√(a(a+2c)))=(√2)a a(a+2c)=2a^2 +(3+2(√2))c^2 −2((√2)+1)c(√(a(a+2c))) a^2 +(3+2(√2))c^2 −2ac=2((√2)+1)c(√(a(a+2c))) [a^2 +(3+2(√2))c^2 −2ac]^2 =4(3+2(√2))a(a+2c)c^2 a^4 +(17+12(√2))c^4 +4a^2 c^2 +2(3+2(√2))a^2 c^2 −4a^3 c−4(3+2(√2))ac^3 =4(3+2(√2))(a^2 c^2 +2ac^3 ) ⇒(17+12(√2))c^4 −6(6+4(√2))ac^3 +4a^2 c^2 −2(3+2(√2))a^2 c^2 −4a^3 c+a^4 =0 ⇒c=...in terms of a (a−b)sin ((45°)/2)=b (a−b)((√(2−(√2)))/2)=b ⇒b=(((√(2−(√2)))a)/(2+(√(2−(√2))))) ....](https://www.tinkutara.com/question/Q54217.png)
$$\frac{{c}}{\mathrm{tan}\:\frac{\mathrm{45}°}{\mathrm{2}}}+\sqrt{\left({a}+{c}\right)^{\mathrm{2}} −{c}^{\mathrm{2}} }=\sqrt{\mathrm{2}}{a} \\ $$$$\Rightarrow\left(\sqrt{\mathrm{2}}+\mathrm{1}\right){c}+\sqrt{{a}\left({a}+\mathrm{2}{c}\right)}=\sqrt{\mathrm{2}}{a} \\ $$$${a}\left({a}+\mathrm{2}{c}\right)=\mathrm{2}{a}^{\mathrm{2}} +\left(\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}\right){c}^{\mathrm{2}} −\mathrm{2}\left(\sqrt{\mathrm{2}}+\mathrm{1}\right){c}\sqrt{{a}\left({a}+\mathrm{2}{c}\right)} \\ $$$${a}^{\mathrm{2}} +\left(\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}\right){c}^{\mathrm{2}} −\mathrm{2}{ac}=\mathrm{2}\left(\sqrt{\mathrm{2}}+\mathrm{1}\right){c}\sqrt{{a}\left({a}+\mathrm{2}{c}\right)} \\ $$$$\left[{a}^{\mathrm{2}} +\left(\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}\right){c}^{\mathrm{2}} −\mathrm{2}{ac}\right]^{\mathrm{2}} =\mathrm{4}\left(\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}\right){a}\left({a}+\mathrm{2}{c}\right){c}^{\mathrm{2}} \\ $$$${a}^{\mathrm{4}} +\left(\mathrm{17}+\mathrm{12}\sqrt{\mathrm{2}}\right){c}^{\mathrm{4}} +\mathrm{4}{a}^{\mathrm{2}} {c}^{\mathrm{2}} +\mathrm{2}\left(\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}\right){a}^{\mathrm{2}} {c}^{\mathrm{2}} −\mathrm{4}{a}^{\mathrm{3}} {c}−\mathrm{4}\left(\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}\right){ac}^{\mathrm{3}} =\mathrm{4}\left(\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}\right)\left({a}^{\mathrm{2}} {c}^{\mathrm{2}} +\mathrm{2}{ac}^{\mathrm{3}} \right) \\ $$$$\Rightarrow\left(\mathrm{17}+\mathrm{12}\sqrt{\mathrm{2}}\right){c}^{\mathrm{4}} −\mathrm{6}\left(\mathrm{6}+\mathrm{4}\sqrt{\mathrm{2}}\right){ac}^{\mathrm{3}} +\mathrm{4}{a}^{\mathrm{2}} {c}^{\mathrm{2}} −\mathrm{2}\left(\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}\right){a}^{\mathrm{2}} {c}^{\mathrm{2}} −\mathrm{4}{a}^{\mathrm{3}} {c}+{a}^{\mathrm{4}} =\mathrm{0} \\ $$$$\Rightarrow{c}=…{in}\:{terms}\:{of}\:{a} \\ $$$$ \\ $$$$\left({a}−{b}\right)\mathrm{sin}\:\frac{\mathrm{45}°}{\mathrm{2}}={b} \\ $$$$\left({a}−{b}\right)\frac{\sqrt{\mathrm{2}−\sqrt{\mathrm{2}}}}{\mathrm{2}}={b} \\ $$$$\Rightarrow{b}=\frac{\sqrt{\mathrm{2}−\sqrt{\mathrm{2}}}{a}}{\mathrm{2}+\sqrt{\mathrm{2}−\sqrt{\mathrm{2}}}} \\ $$$$…. \\ $$
Commented by ajfour last updated on 31/Jan/19

$$\left(\sqrt{\mathrm{2}}+\mathrm{1}\right){c}+\sqrt{{a}\left({a}+\mathrm{2}{c}\right)}=\sqrt{\mathrm{2}}{a} \\ $$$${let}\:\:{a}+\mathrm{2}{c}\:=\:{at}^{\mathrm{2}} \\ $$$$\Rightarrow\:{a}\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)\left({t}^{\mathrm{2}} −\mathrm{1}\right)+\mathrm{2}{at}=\mathrm{2}\sqrt{\mathrm{2}}{a} \\ $$$$\Rightarrow\:\left(\sqrt{\mathrm{2}}+\mathrm{1}\right){t}^{\mathrm{2}} +\mathrm{2}{t}−\mathrm{2}\sqrt{\mathrm{2}}−\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow\:{t}=\:\frac{−\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{2}\sqrt{\mathrm{2}}\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)+\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)^{\mathrm{2}} }}{\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)} \\ $$$$\:\:\:\:\:\:=\:\frac{−\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{4}+\mathrm{2}\sqrt{\mathrm{2}}+\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}}}{\:\sqrt{\mathrm{2}}+\mathrm{1}} \\ $$$$\:\:\:\:\:{t}\:=\:\frac{−\mathrm{1}+\mathrm{2}\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}}{\:\sqrt{\mathrm{2}}+\mathrm{1}} \\ $$$$\Rightarrow\:{t}^{\mathrm{2}} −\mathrm{1}=\frac{\mathrm{1}+\mathrm{8}+\mathrm{4}\sqrt{\mathrm{2}}−\mathrm{4}\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}}{\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}}−\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{6}+\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{4}\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}}{\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$$\:\boldsymbol{{c}}\:=\:\frac{\boldsymbol{{a}}}{\mathrm{2}}\left({t}^{\mathrm{2}} −\mathrm{1}\right)=\:\boldsymbol{{a}}\left(\frac{\mathrm{3}+\sqrt{\mathrm{2}}−\mathrm{2}\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}}{\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}}\right) \\ $$$$\left(\:\:{c}\:\approx\:\mathrm{0}.\mathrm{12331}{a}\right) \\ $$$$….{please}\:{check}\:\:{Sir},\:\:{b}=\frac{{a}\sqrt{\mathrm{2}−\sqrt{\mathrm{2}}}}{\mathrm{2}+\sqrt{\mathrm{2}−\sqrt{\mathrm{2}}}}\: \\ $$$$\:{or}\:\:\:\:{b}\:=\:\frac{\sqrt{\mathrm{2}}{a}}{\mathrm{2}\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}+\sqrt{\mathrm{2}}}\:\:. \\ $$
Commented by mr W last updated on 31/Jan/19
$${very}\:{very}\:{fine}\:{sir}! \\ $$
Commented by ajfour last updated on 31/Jan/19
![thanks, not much remains to be done, Sir. A = (b+c)[a(√2)−((√2)+1)(b+c)].](https://www.tinkutara.com/question/Q54223.png)
$${thanks},\:{not}\:{much}\:{remains}\:{to}\:{be} \\ $$$${done},\:{Sir}. \\ $$$${A}\:=\:\left({b}+{c}\right)\left[{a}\sqrt{\mathrm{2}}−\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)\left({b}+{c}\right)\right]. \\ $$
