Menu Close

Question-54229

Tinku Tara 0 Comments
Pin




Question Number 54229 by ajfour last updated on 31/Jan/19
Commented by ajfour last updated on 31/Jan/19
Find maximum inradius of circle in terms of ellipse parameters a,b.
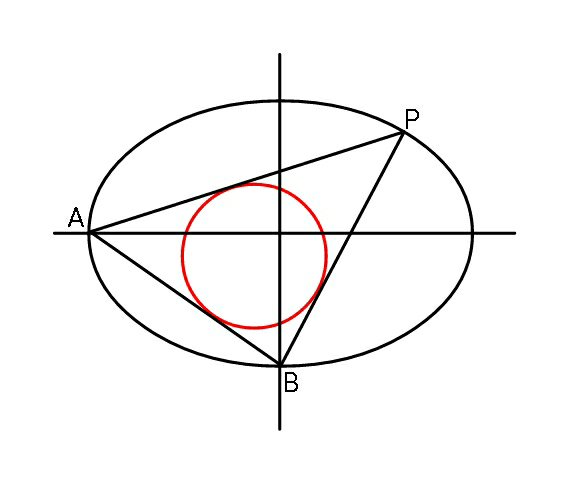
$${Find}\:{maximum}\:{inradius}\:{of}\:{circle} \\ $$$${in}\:{terms}\:{of}\:{ellipse}\:{parameters}\:{a},{b}. \\ $$
Answered by mr W last updated on 01/Feb/19
P(a cos θ, b sin θ) AB=(√(a^2 +b^2 )) eqn. of AB: bx+ay+ab=0 d_⊥ from P to AB=((ab(cos θ+sin θ+1))/( (√(a^2 +b^2 )))) AP=(√(a^2 (cos θ+1)^2 +b^2 sin^2 θ)) BP=(√(a^2 cos^2 θ+b^2 (sin θ+1)^2 )) A_Δ =(r/2)((√(a^2 +b^2 ))+(√(a^2 (cos θ+1)^2 +b^2 sin^2 θ))+(√(a^2 cos^2 θ+b^2 (sin θ+1)^2 )))=(1/2)×(√(a^2 +b^2 ))×((ab(cos θ+sin θ+1))/( (√(a^2 +b^2 )))) r((√(a^2 +b^2 ))+(√(a^2 (cos θ+1)^2 +b^2 sin^2 θ))+(√(a^2 cos^2 θ+b^2 (sin θ+1)^2 )))=ab(cos θ+sin θ+1) ⇒r=((ab(cos θ+sin θ+1))/( (√(a^2 +b^2 ))+(√(a^2 (cos θ+1)^2 +b^2 sin^2 θ))+(√(a^2 cos^2 θ+b^2 (sin θ+1)^2 ))))) with λ=(b/a) ⇒(r/b)=((cos θ+sin θ+1)/( (√(1+λ^2 ))+(√((cos θ+1)^2 +λ^2 sin^2 θ))+(√(cos^2 θ+λ^2 (sin θ+1)^2 ))))) ⇒S=(b/r)=(((√(1+λ^2 ))+(√((cos θ+1)^2 +λ^2 sin^2 θ))+(√(cos^2 θ+λ^2 (sin θ+1)^2 )))/(cos θ+sin θ+1)) (dS/dθ)=0 −(([(√(1+λ^2 ))+(√((cos θ+1)^2 +λ^2 sin^2 θ))+(√(cos^2 θ+λ^2 (sin θ+1)^2 ))](cos θ−sin θ))/((cos θ+sin θ+1)^2 ))+(1/(cos θ+sin θ+1))[((−(cos θ+1)sin θ+λ^2 sin θ cos θ)/( (√((cos θ+1)^2 +λ^2 sin^2 θ))))+((−cos θ sin θ+λ^2 (sin θ+1)cos θ)/( (√(cos^2 θ+λ^2 (sin θ+1)^2 ))))]=0 ⇒(([(√(1+λ^2 ))+(√((cos θ+1)^2 +λ^2 sin^2 θ))+(√(cos^2 θ+λ^2 (sin θ+1)^2 ))](cos θ−sin θ))/(cos θ+sin θ+1))=[(((λ^2 −1)sin θ cos θ−sin θ)/( (√((cos θ+1)^2 +λ^2 sin^2 θ))))+(((λ^2 −1)cos θ sin θ+λ^2 cos θ)/( (√(cos^2 θ+λ^2 (sin θ+1)^2 ))))] ⇒θ=.... examples: λ=(b/a)=1⇒θ=45° λ=(b/a)=0.5⇒θ=71.35° λ=(b/a)=2⇒θ=18.65°
$${P}\left({a}\:\mathrm{cos}\:\theta,\:{b}\:\mathrm{sin}\:\theta\right) \\ $$$${AB}=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$${eqn}.\:{of}\:{AB}: \\ $$$${bx}+{ay}+{ab}=\mathrm{0} \\ $$$${d}_{\bot} \:{from}\:{P}\:{to}\:{AB}=\frac{{ab}\left(\mathrm{cos}\:\theta+\mathrm{sin}\:\theta+\mathrm{1}\right)}{\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }} \\ $$$${AP}=\sqrt{{a}^{\mathrm{2}} \left(\mathrm{cos}\:\theta+\mathrm{1}\right)^{\mathrm{2}} +{b}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta} \\ $$$${BP}=\sqrt{{a}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta+{b}^{\mathrm{2}} \left(\mathrm{sin}\:\theta+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${A}_{\Delta} =\frac{{r}}{\mathrm{2}}\left(\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }+\sqrt{{a}^{\mathrm{2}} \left(\mathrm{cos}\:\theta+\mathrm{1}\right)^{\mathrm{2}} +{b}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta}+\sqrt{{a}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta+{b}^{\mathrm{2}} \left(\mathrm{sin}\:\theta+\mathrm{1}\right)^{\mathrm{2}} }\right)=\frac{\mathrm{1}}{\mathrm{2}}×\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }×\frac{{ab}\left(\mathrm{cos}\:\theta+\mathrm{sin}\:\theta+\mathrm{1}\right)}{\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }} \\ $$$${r}\left(\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }+\sqrt{{a}^{\mathrm{2}} \left(\mathrm{cos}\:\theta+\mathrm{1}\right)^{\mathrm{2}} +{b}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta}+\sqrt{{a}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta+{b}^{\mathrm{2}} \left(\mathrm{sin}\:\theta+\mathrm{1}\right)^{\mathrm{2}} }\right)={ab}\left(\mathrm{cos}\:\theta+\mathrm{sin}\:\theta+\mathrm{1}\right) \\ $$$$\Rightarrow{r}=\frac{{ab}\left(\mathrm{cos}\:\theta+\mathrm{sin}\:\theta+\mathrm{1}\right)}{\left.\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }+\sqrt{{a}^{\mathrm{2}} \left(\mathrm{cos}\:\theta+\mathrm{1}\right)^{\mathrm{2}} +{b}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta}+\sqrt{{a}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta+{b}^{\mathrm{2}} \left(\mathrm{sin}\:\theta+\mathrm{1}\right)^{\mathrm{2}} }\right)} \\ $$$${with}\:\lambda=\frac{{b}}{{a}} \\ $$$$\Rightarrow\frac{{r}}{{b}}=\frac{\mathrm{cos}\:\theta+\mathrm{sin}\:\theta+\mathrm{1}}{\left.\:\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} }+\sqrt{\left(\mathrm{cos}\:\theta+\mathrm{1}\right)^{\mathrm{2}} +\lambda^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta}+\sqrt{\mathrm{cos}^{\mathrm{2}} \:\theta+\lambda^{\mathrm{2}} \left(\mathrm{sin}\:\theta+\mathrm{1}\right)^{\mathrm{2}} }\right)} \\ $$$$\Rightarrow{S}=\frac{{b}}{{r}}=\frac{\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} }+\sqrt{\left(\mathrm{cos}\:\theta+\mathrm{1}\right)^{\mathrm{2}} +\lambda^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta}+\sqrt{\mathrm{cos}^{\mathrm{2}} \:\theta+\lambda^{\mathrm{2}} \left(\mathrm{sin}\:\theta+\mathrm{1}\right)^{\mathrm{2}} }}{\mathrm{cos}\:\theta+\mathrm{sin}\:\theta+\mathrm{1}} \\ $$$$\frac{{dS}}{{d}\theta}=\mathrm{0} \\ $$$$−\frac{\left[\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} }+\sqrt{\left(\mathrm{cos}\:\theta+\mathrm{1}\right)^{\mathrm{2}} +\lambda^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta}+\sqrt{\mathrm{cos}^{\mathrm{2}} \:\theta+\lambda^{\mathrm{2}} \left(\mathrm{sin}\:\theta+\mathrm{1}\right)^{\mathrm{2}} }\right]\left(\mathrm{cos}\:\theta−\mathrm{sin}\:\theta\right)}{\left(\mathrm{cos}\:\theta+\mathrm{sin}\:\theta+\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{cos}\:\theta+\mathrm{sin}\:\theta+\mathrm{1}}\left[\frac{−\left(\mathrm{cos}\:\theta+\mathrm{1}\right)\mathrm{sin}\:\theta+\lambda^{\mathrm{2}} \mathrm{sin}\:\theta\:\mathrm{cos}\:\theta}{\:\sqrt{\left(\mathrm{cos}\:\theta+\mathrm{1}\right)^{\mathrm{2}} +\lambda^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta}}+\frac{−\mathrm{cos}\:\theta\:\mathrm{sin}\:\theta+\lambda^{\mathrm{2}} \left(\mathrm{sin}\:\theta+\mathrm{1}\right)\mathrm{cos}\:\theta}{\:\sqrt{\mathrm{cos}^{\mathrm{2}} \:\theta+\lambda^{\mathrm{2}} \left(\mathrm{sin}\:\theta+\mathrm{1}\right)^{\mathrm{2}} }}\right]=\mathrm{0} \\ $$$$\Rightarrow\frac{\left[\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} }+\sqrt{\left(\mathrm{cos}\:\theta+\mathrm{1}\right)^{\mathrm{2}} +\lambda^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta}+\sqrt{\mathrm{cos}^{\mathrm{2}} \:\theta+\lambda^{\mathrm{2}} \left(\mathrm{sin}\:\theta+\mathrm{1}\right)^{\mathrm{2}} }\right]\left(\mathrm{cos}\:\theta−\mathrm{sin}\:\theta\right)}{\mathrm{cos}\:\theta+\mathrm{sin}\:\theta+\mathrm{1}}=\left[\frac{\left(\lambda^{\mathrm{2}} −\mathrm{1}\right)\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta−\mathrm{sin}\:\theta}{\:\sqrt{\left(\mathrm{cos}\:\theta+\mathrm{1}\right)^{\mathrm{2}} +\lambda^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta}}+\frac{\left(\lambda^{\mathrm{2}} −\mathrm{1}\right)\mathrm{cos}\:\theta\:\mathrm{sin}\:\theta+\lambda^{\mathrm{2}} \mathrm{cos}\:\theta}{\:\sqrt{\mathrm{cos}^{\mathrm{2}} \:\theta+\lambda^{\mathrm{2}} \left(\mathrm{sin}\:\theta+\mathrm{1}\right)^{\mathrm{2}} }}\right] \\ $$$$\Rightarrow\theta=…. \\ $$$${examples}: \\ $$$$\lambda=\frac{{b}}{{a}}=\mathrm{1}\Rightarrow\theta=\mathrm{45}° \\ $$$$\lambda=\frac{{b}}{{a}}=\mathrm{0}.\mathrm{5}\Rightarrow\theta=\mathrm{71}.\mathrm{35}° \\ $$$$\lambda=\frac{{b}}{{a}}=\mathrm{2}\Rightarrow\theta=\mathrm{18}.\mathrm{65}° \\ $$
Commented by ajfour last updated on 01/Feb/19
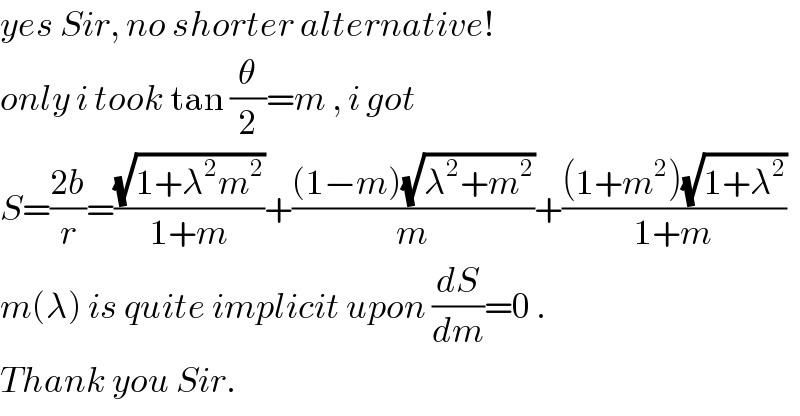
yes Sir, no shorter alternative! only i took tan (θ/2)=m , i got S=((2b)/r)=((√(1+λ^2 m^2 ))/(1+m))+(((1−m)(√(λ^2 +m^2 )))/m)+(((1+m^2 )(√(1+λ^2 )))/(1+m)) m(λ) is quite implicit upon (dS/dm)=0 . Thank you Sir.
$${yes}\:{Sir},\:{no}\:{shorter}\:{alternative}! \\ $$$${only}\:{i}\:{took}\:\mathrm{tan}\:\frac{\theta}{\mathrm{2}}={m}\:,\:{i}\:{got} \\ $$$${S}=\frac{\mathrm{2}{b}}{{r}}=\frac{\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} {m}^{\mathrm{2}} }}{\mathrm{1}+{m}}+\frac{\left(\mathrm{1}−{m}\right)\sqrt{\lambda^{\mathrm{2}} +{m}^{\mathrm{2}} }}{{m}}+\frac{\left(\mathrm{1}+{m}^{\mathrm{2}} \right)\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} }}{\mathrm{1}+{m}} \\ $$$${m}\left(\lambda\right)\:{is}\:{quite}\:{implicit}\:{upon}\:\frac{{dS}}{{dm}}=\mathrm{0}\:. \\ $$$${Thank}\:{you}\:{Sir}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *