Question Number 54239 by 951172235v last updated on 01/Feb/19
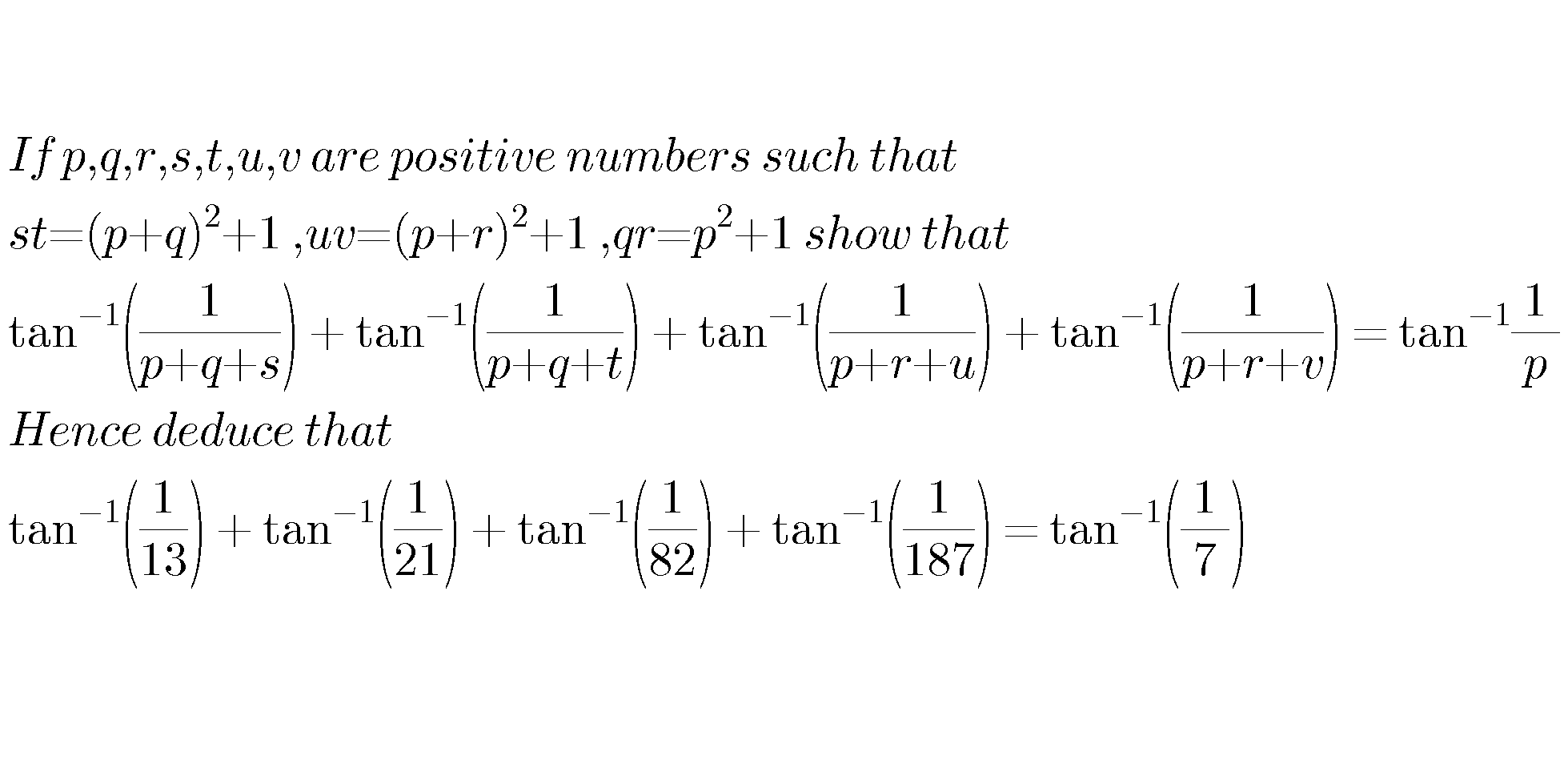
Answered by Prithwish sen last updated on 01/Feb/19

$$=\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\frac{\mathrm{1}}{\mathrm{p}+\mathrm{q}+\mathrm{s}}\:+\frac{\mathrm{1}}{\mathrm{p}+\mathrm{q}+\mathrm{t}}}{\mathrm{1}−\:\frac{\mathrm{1}}{\left(\mathrm{p}+\mathrm{q}+\mathrm{s}\right)\left(\mathrm{p}+\mathrm{q}+\mathrm{t}\right)}}\right)\:+ \\ $$$$\mathrm{tan}^{−\mathrm{1}} \left(\frac{\frac{\mathrm{1}}{\mathrm{p}+\mathrm{r}+\mathrm{u}}\:+\frac{\mathrm{1}}{\mathrm{p}+\mathrm{r}+\mathrm{v}}}{\mathrm{1}−\frac{\mathrm{1}}{\left(\mathrm{p}+\mathrm{r}+\mathrm{u}\right)\left(\mathrm{p}+\mathrm{r}+\mathrm{v}\right)}}\:\right) \\ $$$$=\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2p}+\mathrm{2q}+\mathrm{s}+\mathrm{t}}{\left(\mathrm{p}+\mathrm{q}\right)^{\mathrm{2}} \:+\:\left(\mathrm{p}+\mathrm{q}\right)\left(\mathrm{s}+\mathrm{t}\right)+\mathrm{st}\:−\mathrm{1}}\:\right)\:+ \\ $$$$\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2p}+\mathrm{2r}+\mathrm{u}+\mathrm{v}}{\left(\mathrm{p}+\mathrm{r}\right)^{\mathrm{2}} +\left(\mathrm{p}+\mathrm{r}\right)\left(\mathrm{u}+\mathrm{v}\right)+\mathrm{uv}\:−\mathrm{1}}\right) \\ $$$$=\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2p}+\mathrm{2q}+\mathrm{s}+\mathrm{t}}{\mathrm{2}\left(\mathrm{p}+\mathrm{q}\right)^{\mathrm{2}} +\left(\mathrm{p}+\mathrm{q}\right)\left(\mathrm{s}+\mathrm{t}\right)}\right)\:+ \\ $$$$\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2p}+\mathrm{2r}+\mathrm{u}+\mathrm{v}}{\mathrm{2}\left(\mathrm{p}+\mathrm{r}\right)^{\mathrm{2}} +\left(\mathrm{p}+\mathrm{r}\right)\left(\mathrm{u}+\mathrm{v}\right)}\right) \\ $$$$=\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\left(\mathrm{p}+\mathrm{q}\right)}\right)\:+\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\left(\mathrm{p}+\mathrm{r}\right)}\right) \\ $$$$=\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2p}+\mathrm{q}+\mathrm{r}}{\mathrm{p}^{\mathrm{2}} +\mathrm{pr}+\mathrm{pq}+\mathrm{qr}−\mathrm{1}}\right) \\ $$$$=\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2p}+\mathrm{q}+\mathrm{r}}{\mathrm{2p}^{\mathrm{2}} +\mathrm{pq}+\mathrm{pr}}\right) \\ $$$$=\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{p}}\right) \\ $$$$\mathrm{Hence}\:\mathrm{proved}. \\ $$
