Menu Close

Question-54242

Tinku Tara 0 Comments
Pin




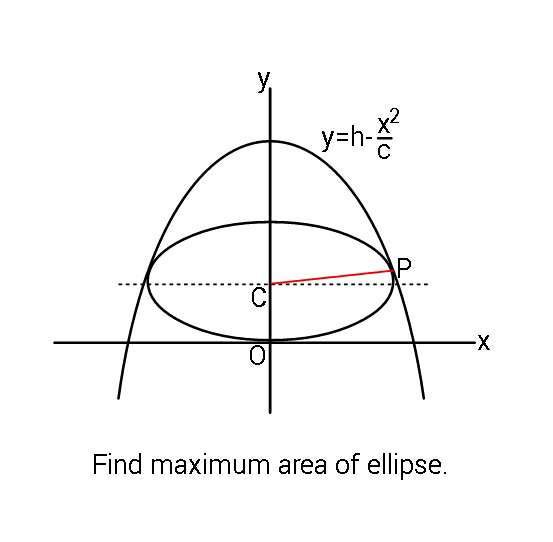
Question Number 54242 by ajfour last updated on 01/Feb/19
Answered by mr W last updated on 01/Feb/19
parabola: y=h−(x^2 /c) ellipse: (x^2 /a^2 )+(((y−b)^2 )/b^2 )=1 intersection: ((c(h−y))/a^2 )+(((y−b)^2 )/b^2 )=1 cb^2 (h−y)+a^2 (y−b)^2 =a^2 b^2 a^2 y^2 −(2a^2 +cb)by+chb^2 =0 D=(2a^2 +cb)^2 b^2 −4a^2 chb^2 =0 (2a^2 +cb)^2 −4a^2 ch=0 ⇒b=((2a)/c)((√(ch))−a) A=πab=((2π)/c)a^2 ((√(ch))−a) (dA/da)=0 ⇒2a(√(ch))−3a^2 =0 ⇒a=((2(√(ch)))/3) ⇒b=(2/c)×((2(√(ch)))/3)((√(ch))−((2(√(ch)))/3))=((4h)/9) A_(max) =πab=((8πh(√(ch)))/(27))
$${parabola}: \\ $$$${y}={h}−\frac{{x}^{\mathrm{2}} }{{c}} \\ $$$${ellipse}: \\ $$$$\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{\left({y}−{b}\right)^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$${intersection}: \\ $$$$\frac{{c}\left({h}−{y}\right)}{{a}^{\mathrm{2}} }+\frac{\left({y}−{b}\right)^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$${cb}^{\mathrm{2}} \left({h}−{y}\right)+{a}^{\mathrm{2}} \left({y}−{b}\right)^{\mathrm{2}} ={a}^{\mathrm{2}} {b}^{\mathrm{2}} \\ $$$${a}^{\mathrm{2}} {y}^{\mathrm{2}} −\left(\mathrm{2}{a}^{\mathrm{2}} +{cb}\right){by}+{chb}^{\mathrm{2}} =\mathrm{0} \\ $$$${D}=\left(\mathrm{2}{a}^{\mathrm{2}} +{cb}\right)^{\mathrm{2}} {b}^{\mathrm{2}} −\mathrm{4}{a}^{\mathrm{2}} {chb}^{\mathrm{2}} =\mathrm{0} \\ $$$$\left(\mathrm{2}{a}^{\mathrm{2}} +{cb}\right)^{\mathrm{2}} −\mathrm{4}{a}^{\mathrm{2}} {ch}=\mathrm{0} \\ $$$$\Rightarrow{b}=\frac{\mathrm{2}{a}}{{c}}\left(\sqrt{{ch}}−{a}\right) \\ $$$${A}=\pi{ab}=\frac{\mathrm{2}\pi}{{c}}{a}^{\mathrm{2}} \left(\sqrt{{ch}}−{a}\right) \\ $$$$\frac{{dA}}{{da}}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{2}{a}\sqrt{{ch}}−\mathrm{3}{a}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{a}=\frac{\mathrm{2}\sqrt{{ch}}}{\mathrm{3}} \\ $$$$\Rightarrow{b}=\frac{\mathrm{2}}{{c}}×\frac{\mathrm{2}\sqrt{{ch}}}{\mathrm{3}}\left(\sqrt{{ch}}−\frac{\mathrm{2}\sqrt{{ch}}}{\mathrm{3}}\right)=\frac{\mathrm{4}{h}}{\mathrm{9}} \\ $$$${A}_{{max}} =\pi{ab}=\frac{\mathrm{8}\pi{h}\sqrt{{ch}}}{\mathrm{27}} \\ $$
Commented by ajfour last updated on 01/Feb/19
THANK YOU SIR.
$$\mathcal{THANK}\:\mathcal{YOU}\:\:\mathbb{SIR}. \\ $$
Answered by ajfour last updated on 01/Feb/19
let C be origin. eq. of parabola: y=h−b−(x^2 /c) let P (acos θ, bsin θ) (dy/dx)∣_P = −((bcos θ)/(asin θ )) = −((2x)/c) =−((2acos θ)/c) ⇒ a^2 = ((bc)/(2sin θ)) ....(i) bsin θ = h−b−((a^2 cos^2 θ)/c) using (i) herein bsin θ=h−b−((bcos^2 θ)/(2sin θ)) ⇒ 2bsin^2 θ=2hsin θ−2bsin θ−bcos^2 θ ⇒ b(sin^2 θ+2sin θ+1)=2hsin θ ⇒ b=((2hsin θ)/((1+sin θ)^2 )) and using (i) ⇒ a^2 =((ch)/((1+sin θ)^2 )) ⇒ a=((√(ch))/(1+sin θ)) ⇒ A=πab = ((2πh(√(ch))sin θ)/((1+sin θ)^3 )) .....(ii) let S= ((sin θ)/((1+sin θ)^3 )) (dS/dθ)=0 ⇒ cos θ(1+sin θ)^3 =3sin θcos θ(1+sin θ)^2 ⇒ 1+sin θ = 3sin θ or sin θ = 1/2 ⇒ S = (4/(27)) ⇒ A_(max) = ((8πh(√(ch)))/(27)) . (parametric isn′t wrong either!)
$${let}\:{C}\:{be}\:{origin}. \\ $$$${eq}.\:{of}\:{parabola}:\:\:\:{y}=\boldsymbol{{h}}−{b}−\frac{{x}^{\mathrm{2}} }{{c}} \\ $$$${let}\:{P}\:\left({a}\mathrm{cos}\:\theta,\:{b}\mathrm{sin}\:\theta\right) \\ $$$$\frac{{dy}}{{dx}}\mid_{{P}} =\:−\frac{{b}\mathrm{cos}\:\theta}{{a}\mathrm{sin}\:\theta\:}\:=\:−\frac{\mathrm{2}{x}}{{c}}\:=−\frac{\mathrm{2}{a}\mathrm{cos}\:\theta}{{c}} \\ $$$$\Rightarrow\:\:\:\:{a}^{\mathrm{2}} =\:\frac{{bc}}{\mathrm{2sin}\:\theta}\:\:\:\:\:….\left({i}\right) \\ $$$${b}\mathrm{sin}\:\theta\:=\:\boldsymbol{{h}}−{b}−\frac{{a}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \theta}{{c}} \\ $$$${using}\:\left({i}\right)\:{herein} \\ $$$$\:\:\:{b}\mathrm{sin}\:\theta=\boldsymbol{{h}}−{b}−\frac{{b}\mathrm{cos}\:^{\mathrm{2}} \theta}{\mathrm{2sin}\:\theta} \\ $$$$\Rightarrow\:\:\mathrm{2}{b}\mathrm{sin}\:^{\mathrm{2}} \theta=\mathrm{2}\boldsymbol{{h}}\mathrm{sin}\:\theta−\mathrm{2}{b}\mathrm{sin}\:\theta−{b}\mathrm{cos}\:^{\mathrm{2}} \theta \\ $$$$\Rightarrow\:{b}\left(\mathrm{sin}\:^{\mathrm{2}} \theta+\mathrm{2sin}\:\theta+\mathrm{1}\right)=\mathrm{2}\boldsymbol{{h}}\mathrm{sin}\:\theta \\ $$$$\Rightarrow\:\:{b}=\frac{\mathrm{2}\boldsymbol{{h}}\mathrm{sin}\:\theta}{\left(\mathrm{1}+\mathrm{sin}\:\theta\right)^{\mathrm{2}} }\:\:\:\:\:{and}\:{using}\:\left({i}\right) \\ $$$$\Rightarrow\:\:{a}^{\mathrm{2}} =\frac{{c}\boldsymbol{{h}}}{\left(\mathrm{1}+\mathrm{sin}\:\theta\right)^{\mathrm{2}} } \\ $$$$\Rightarrow\:\:{a}=\frac{\sqrt{{c}\boldsymbol{{h}}}}{\mathrm{1}+\mathrm{sin}\:\theta}\:\:\: \\ $$$$\Rightarrow\:\:\:{A}=\pi{ab}\:=\:\frac{\mathrm{2}\pi{h}\sqrt{{ch}}\mathrm{sin}\:\theta}{\left(\mathrm{1}+\mathrm{sin}\:\theta\right)^{\mathrm{3}} }\:\:\:…..\left({ii}\right) \\ $$$${let}\:\:{S}=\:\frac{\mathrm{sin}\:\theta}{\left(\mathrm{1}+\mathrm{sin}\:\theta\right)^{\mathrm{3}} } \\ $$$$\frac{{dS}}{{d}\theta}=\mathrm{0}\:\:\:\Rightarrow \\ $$$$\mathrm{cos}\:\theta\left(\mathrm{1}+\mathrm{sin}\:\theta\right)^{\mathrm{3}} =\mathrm{3sin}\:\theta\mathrm{cos}\:\theta\left(\mathrm{1}+\mathrm{sin}\:\theta\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\mathrm{1}+\mathrm{sin}\:\theta\:=\:\mathrm{3sin}\:\theta \\ $$$${or}\:\:\:\:\:\mathrm{sin}\:\theta\:=\:\mathrm{1}/\mathrm{2}\:\:\Rightarrow\:{S}\:=\:\frac{\mathrm{4}}{\mathrm{27}}\:\:\: \\ $$$$\Rightarrow\:\:\:\:{A}_{{max}} =\:\frac{\mathrm{8}\pi\boldsymbol{{h}}\sqrt{{c}\boldsymbol{{h}}}}{\mathrm{27}}\:. \\ $$$$\left({parametric}\:{isn}'{t}\:{wrong}\:{either}!\right) \\ $$
Commented by mr W last updated on 01/Feb/19
nice too!
$${nice}\:{too}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *