Question Number 54248 by rahul 19 last updated on 01/Feb/19

Commented by rahul 19 last updated on 01/Feb/19
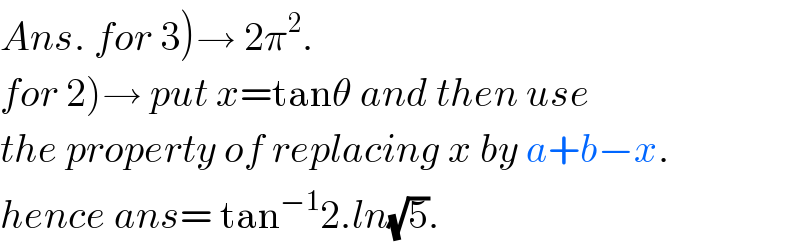
$$\left.{Ans}.\:{for}\:\mathrm{3}\right)\rightarrow\:\mathrm{2}\pi^{\mathrm{2}} . \\ $$$$\left.{for}\:\mathrm{2}\right)\rightarrow\:{put}\:{x}=\mathrm{tan}\theta\:{and}\:{then}\:{use} \\ $$$${the}\:{property}\:{of}\:{replacing}\:{x}\:{by}\:{a}+{b}−{x}. \\ $$$${hence}\:{ans}=\:\mathrm{tan}^{−\mathrm{1}} \mathrm{2}.{ln}\sqrt{\mathrm{5}}. \\ $$
Answered by rahul 19 last updated on 01/Feb/19
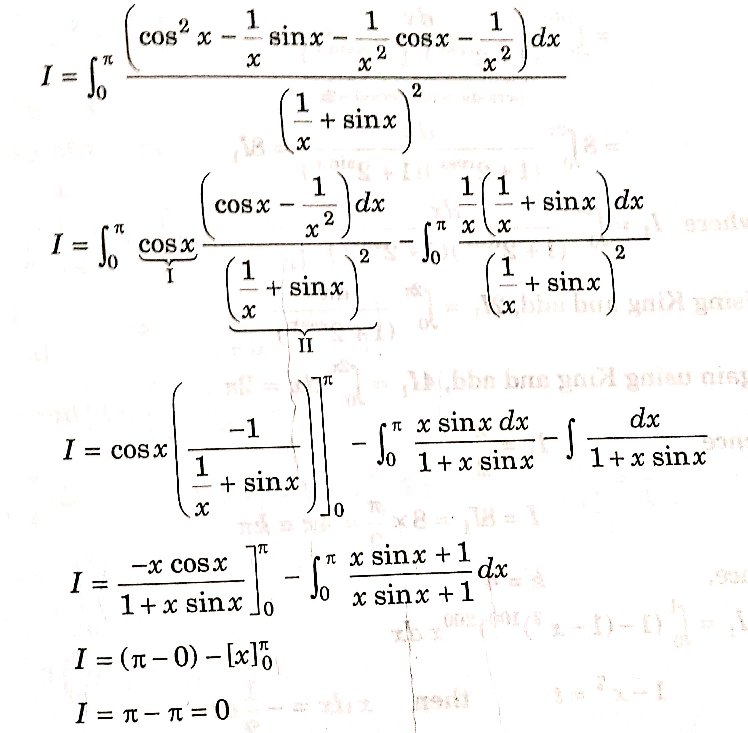
Commented by Meritguide1234 last updated on 01/Feb/19
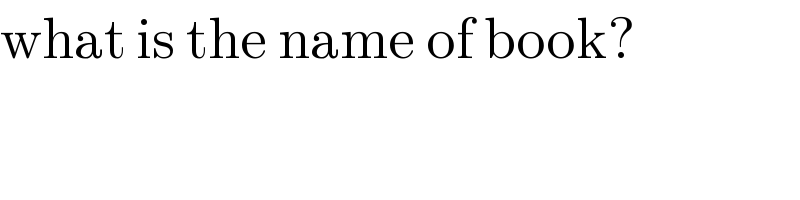
$$\mathrm{what}\:\mathrm{is}\:\mathrm{the}\:\mathrm{name}\:\mathrm{of}\:\mathrm{book}? \\ $$
Commented by rahul 19 last updated on 01/Feb/19
grb problems in calculus for JEE.
Answered by Prithwish sen last updated on 01/Feb/19
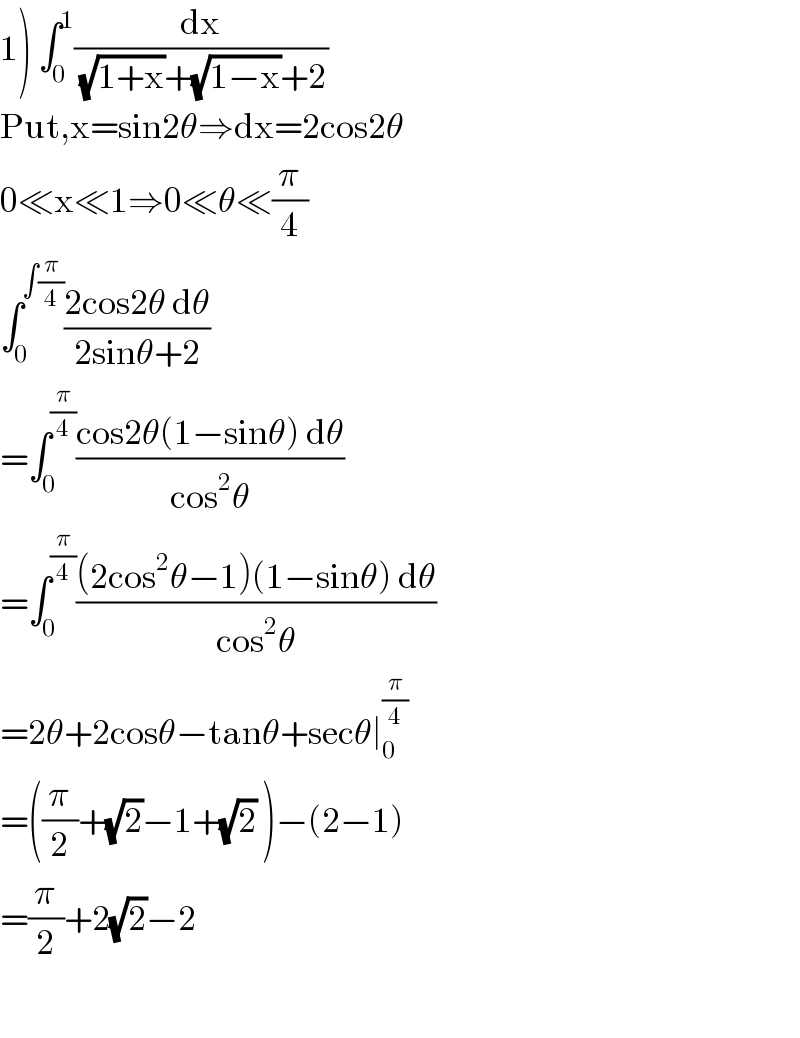
$$\left.\mathrm{1}\right)\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{dx}}{\:\sqrt{\mathrm{1}+\mathrm{x}}+\sqrt{\mathrm{1}−\mathrm{x}}+\mathrm{2}} \\ $$$$\mathrm{Put},\mathrm{x}=\mathrm{sin2}\theta\Rightarrow\mathrm{dx}=\mathrm{2cos2}\theta \\ $$$$\mathrm{0}\ll\mathrm{x}\ll\mathrm{1}\Rightarrow\mathrm{0}\ll\theta\ll\frac{\pi}{\mathrm{4}} \\ $$$$\int_{\mathrm{0}} ^{\int\frac{\pi}{\mathrm{4}}} \frac{\mathrm{2cos2}\theta\:\mathrm{d}\theta}{\mathrm{2sin}\theta+\mathrm{2}} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{\mathrm{cos2}\theta\left(\mathrm{1}−\mathrm{sin}\theta\right)\:\mathrm{d}\theta}{\mathrm{cos}^{\mathrm{2}} \theta} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{\left(\mathrm{2cos}^{\mathrm{2}} \theta−\mathrm{1}\right)\left(\mathrm{1}−\mathrm{sin}\theta\right)\:\mathrm{d}\theta}{\mathrm{cos}^{\mathrm{2}} \theta} \\ $$$$=\mathrm{2}\theta+\mathrm{2cos}\theta−\mathrm{tan}\theta+\mathrm{sec}\theta\mid_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \\ $$$$=\left(\frac{\pi}{\mathrm{2}}+\sqrt{\mathrm{2}}−\mathrm{1}+\sqrt{\mathrm{2}}\:\right)−\left(\mathrm{2}−\mathrm{1}\right) \\ $$$$=\frac{\pi}{\mathrm{2}}+\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{2}\: \\ $$$$ \\ $$
