Question Number 54271 by naveen200601 last updated on 01/Feb/19
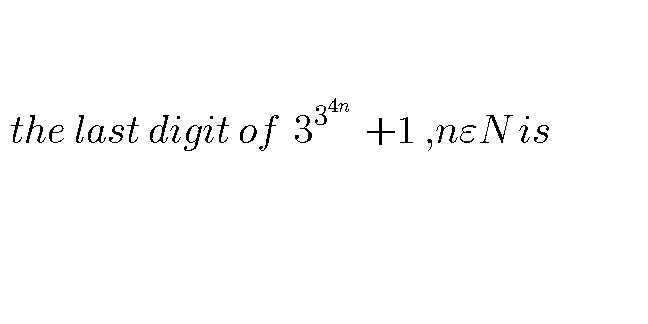
Commented by Meritguide1234 last updated on 02/Feb/19

$$\mathrm{post}\:\mathrm{many}\:\mathrm{problem}\:\mathrm{on}\:\mathrm{this}\:\mathrm{type} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 01/Feb/19

$$\mathrm{3}^{\mathrm{4}} =\mathrm{81} \\ $$$$\mathrm{3}^{\mathrm{1}} =\mathrm{3} \\ $$$$\mathrm{3}^{\mathrm{2}} =\mathrm{9} \\ $$$$\mathrm{3}^{\mathrm{3}} =\mathrm{27} \\ $$$$\mathrm{3}^{\mathrm{4}} =\mathrm{81} \\ $$$$\mathrm{3}^{\mathrm{5}} =\mathrm{243} \\ $$$$\mathrm{3}^{\mathrm{6}} =\mathrm{729} \\ $$$$…{thus} \\ $$$${last}\:{digit}\:\left(\mathrm{3},\mathrm{9},\mathrm{7},\mathrm{1}\right)\:{is}\:{repeating}\:{in}\:{cycle}\:{wise}.. \\ $$$$\mathrm{3}^{\mathrm{4}{n}} =\left(\mathrm{81}\right)^{{n}} =\left(\mathrm{1}+\mathrm{80}\right)^{{n}} \\ $$$$\mathrm{1}+{nc}_{\mathrm{1}} \mathrm{80}+{nc}_{\mathrm{2}} \mathrm{80}^{\mathrm{2}} +{nc}_{\mathrm{3}} \mathrm{80}^{\mathrm{3}} +…+\mathrm{80}^{{n}} \\ $$$$\mathrm{3}^{\mathrm{3}^{\mathrm{4}{n}} } \\ $$$$=\mathrm{3}^{\left(\mathrm{1}+{nc}_{\mathrm{1}} \mathrm{80}+{nc}_{\mathrm{2}} \mathrm{80}^{\mathrm{2}} +{nc}_{\mathrm{3}} \mathrm{80}^{\mathrm{3}} +…+\mathrm{80}^{{n}} \right.} \\ $$$$=\mathrm{3}^{\mathrm{1}} ×\mathrm{3}^{{nc}_{\mathrm{1}} \mathrm{80}} ×\mathrm{3}^{{nc}_{\mathrm{2}} \mathrm{80}^{\mathrm{2}} } …×\mathrm{3}^{\mathrm{80}^{{n}} } \\ $$$$=\left({unit}\:{place}\:\mathrm{3}\right)×\left({unit}\:{place}\:\mathrm{1}\right)\left({u}.{p}\:\mathrm{1}\right)…\left({u}.{p}\:\mathrm{1}\right) \\ $$$$={so}\:{unit}\:{place}\:{is}\:\mathrm{3} \\ $$$${so}\:{u}.{p}\:{of}\:\mathrm{3}^{\mathrm{3}^{\mathrm{4}{n}} } +\mathrm{1}=\mathrm{3}+\mathrm{1}=\mathrm{4} \\ $$
