Question Number 54312 by ajfour last updated on 02/Feb/19
Commented by ajfour last updated on 02/Feb/19
Commented by ajfour last updated on 02/Feb/19
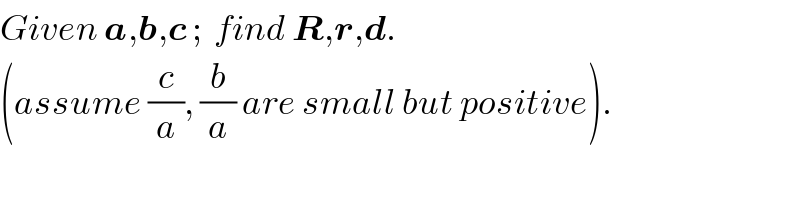
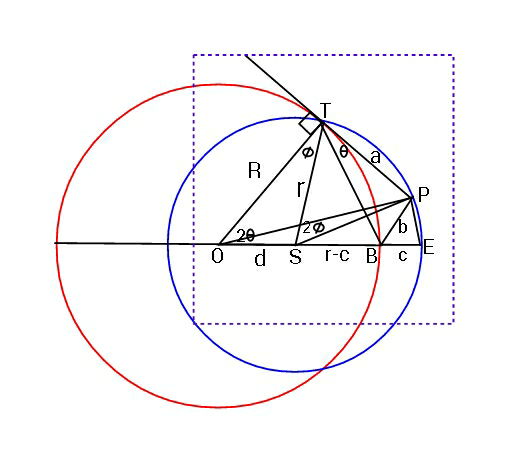
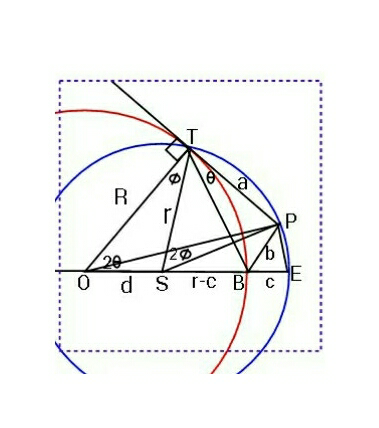
$${Given}\:\boldsymbol{{a}},\boldsymbol{{b}},\boldsymbol{{c}}\:;\:\:{find}\:\boldsymbol{{R}},\boldsymbol{{r}},\boldsymbol{{d}}. \\ $$$$\left({assume}\:\frac{{c}}{{a}},\:\frac{{b}}{{a}}\:{are}\:{small}\:{but}\:{positive}\right). \\ $$
Answered by ajfour last updated on 02/Feb/19

$${matter}\:{of}\:{four}\:{eqs}. \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$$\begin{cases}{{R}\mathrm{sin}\:\mathrm{2}\theta=\sqrt{{r}^{\mathrm{2}} −\frac{{a}^{\mathrm{2}} }{\mathrm{4}}}\:\mathrm{sin}\:\mathrm{2}\theta+\frac{{a}}{\mathrm{2}}\mathrm{cos}\:\mathrm{2}\theta}\\{\frac{{a}}{\mathrm{2sin}\:\mathrm{2}\theta}={R}−{r}+{c}}\\{\mathrm{2}{R}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{cos}\:\mathrm{2}\theta\right)−\mathrm{2}{aR}\mathrm{sin}\:\mathrm{2}\theta+{a}^{\mathrm{2}} −{b}^{\mathrm{2}} =\mathrm{0}}\\{{d}=\frac{{a}}{\mathrm{2sin}\:\mathrm{2}\theta}}\end{cases} \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_. \\ $$
