Question Number 54334 by ajfour last updated on 02/Feb/19

Commented by ajfour last updated on 02/Feb/19
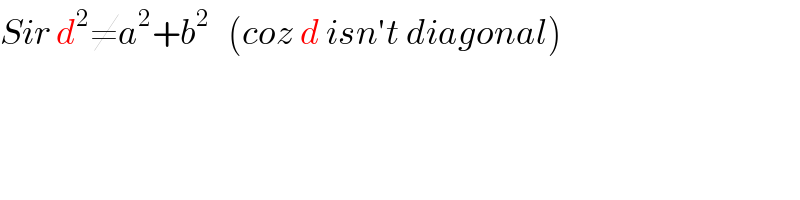
$${Sir}\:{d}^{\mathrm{2}} \neq{a}^{\mathrm{2}} +{b}^{\mathrm{2}} \:\:\:\left({coz}\:{d}\:{isn}'{t}\:{diagonal}\right) \\ $$
Answered by mr W last updated on 02/Feb/19
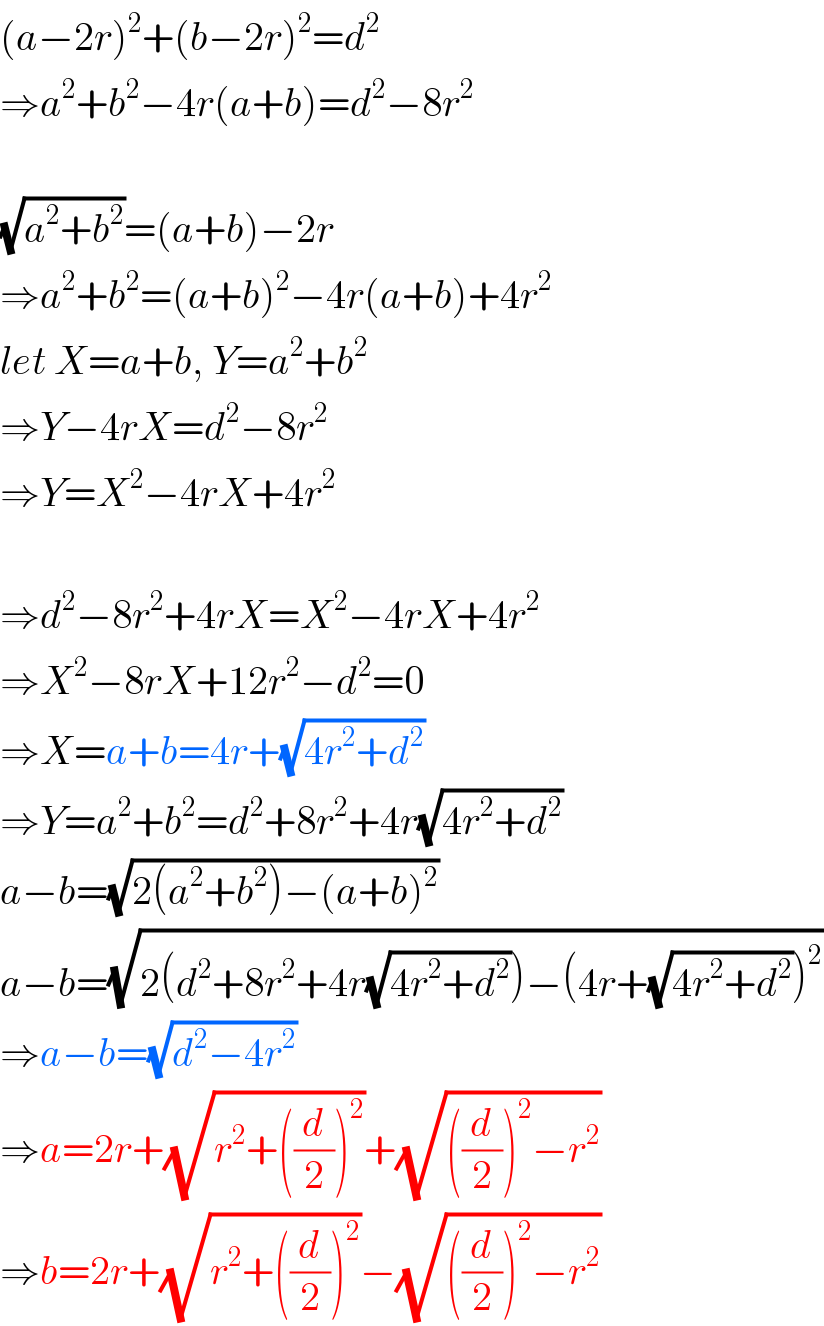
$$\left({a}−\mathrm{2}{r}\right)^{\mathrm{2}} +\left({b}−\mathrm{2}{r}\right)^{\mathrm{2}} ={d}^{\mathrm{2}} \\ $$$$\Rightarrow{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{4}{r}\left({a}+{b}\right)={d}^{\mathrm{2}} −\mathrm{8}{r}^{\mathrm{2}} \\ $$$$ \\ $$$$\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }=\left({a}+{b}\right)−\mathrm{2}{r} \\ $$$$\Rightarrow{a}^{\mathrm{2}} +{b}^{\mathrm{2}} =\left({a}+{b}\right)^{\mathrm{2}} −\mathrm{4}{r}\left({a}+{b}\right)+\mathrm{4}{r}^{\mathrm{2}} \\ $$$${let}\:{X}={a}+{b},\:{Y}={a}^{\mathrm{2}} +{b}^{\mathrm{2}} \\ $$$$\Rightarrow{Y}−\mathrm{4}{rX}={d}^{\mathrm{2}} −\mathrm{8}{r}^{\mathrm{2}} \\ $$$$\Rightarrow{Y}={X}^{\mathrm{2}} −\mathrm{4}{rX}+\mathrm{4}{r}^{\mathrm{2}} \\ $$$$ \\ $$$$\Rightarrow{d}^{\mathrm{2}} −\mathrm{8}{r}^{\mathrm{2}} +\mathrm{4}{rX}={X}^{\mathrm{2}} −\mathrm{4}{rX}+\mathrm{4}{r}^{\mathrm{2}} \\ $$$$\Rightarrow{X}^{\mathrm{2}} −\mathrm{8}{rX}+\mathrm{12}{r}^{\mathrm{2}} −{d}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{X}={a}+{b}=\mathrm{4}{r}+\sqrt{\mathrm{4}{r}^{\mathrm{2}} +{d}^{\mathrm{2}} } \\ $$$$\Rightarrow{Y}={a}^{\mathrm{2}} +{b}^{\mathrm{2}} ={d}^{\mathrm{2}} +\mathrm{8}{r}^{\mathrm{2}} +\mathrm{4}{r}\sqrt{\mathrm{4}{r}^{\mathrm{2}} +{d}^{\mathrm{2}} } \\ $$$${a}−{b}=\sqrt{\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)−\left({a}+{b}\right)^{\mathrm{2}} } \\ $$$${a}−{b}=\sqrt{\mathrm{2}\left({d}^{\mathrm{2}} +\mathrm{8}{r}^{\mathrm{2}} +\mathrm{4}{r}\sqrt{\mathrm{4}{r}^{\mathrm{2}} +{d}^{\mathrm{2}} }\right)−\left(\mathrm{4}{r}+\sqrt{\mathrm{4}{r}^{\mathrm{2}} +{d}^{\mathrm{2}} }\right)^{\mathrm{2}} } \\ $$$$\Rightarrow{a}−{b}=\sqrt{{d}^{\mathrm{2}} −\mathrm{4}{r}^{\mathrm{2}} } \\ $$$$\Rightarrow{a}=\mathrm{2}{r}+\sqrt{{r}^{\mathrm{2}} +\left(\frac{{d}}{\mathrm{2}}\right)^{\mathrm{2}} }+\sqrt{\left(\frac{{d}}{\mathrm{2}}\right)^{\mathrm{2}} −{r}^{\mathrm{2}} } \\ $$$$\Rightarrow{b}=\mathrm{2}{r}+\sqrt{{r}^{\mathrm{2}} +\left(\frac{{d}}{\mathrm{2}}\right)^{\mathrm{2}} }−\sqrt{\left(\frac{{d}}{\mathrm{2}}\right)^{\mathrm{2}} −{r}^{\mathrm{2}} } \\ $$
Commented by ajfour last updated on 02/Feb/19
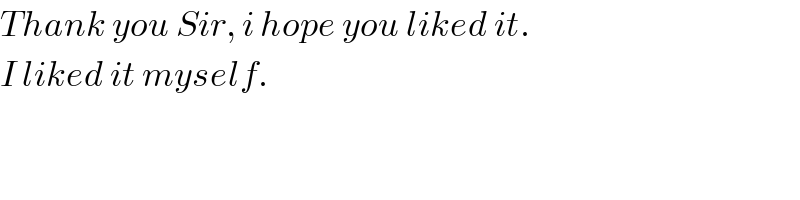
$${Thank}\:{you}\:{Sir},\:{i}\:{hope}\:{you}\:{liked}\:{it}. \\ $$$${I}\:{liked}\:{it}\:{myself}. \\ $$
Commented by mr W last updated on 02/Feb/19

$${like}\:{all}\:{others}\:{of}\:{yours},\:{this}\:{is}\:{also}\:{a} \\ $$$${nice}\:{and}\:{interesting}\:{question}\:{sir}! \\ $$
Commented by ajfour last updated on 02/Feb/19

$${Thanks}\:{for}\:{the}\:{appreciation},\:{Sir}, \\ $$$${thats}\:{how}\:{i}\:{learn}\:{from}\:{you}. \\ $$
Commented by Rasheed.Sindhi last updated on 03/Feb/19

$${Sir}\:{Mr}\:{W},\:{I}\:{didn}'{t}\:{understand}\:{the} \\ $$$$\mathrm{3}{rd}\:{line}:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }=\left({a}+{b}\right)−\mathrm{2}{r} \\ $$$${Pl}\:{explain}. \\ $$
Commented by mr W last updated on 03/Feb/19

Commented by mr W last updated on 03/Feb/19
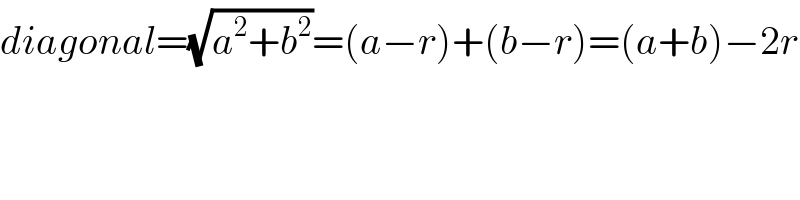
$${diagonal}=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }=\left({a}−{r}\right)+\left({b}−{r}\right)=\left({a}+{b}\right)−\mathrm{2}{r} \\ $$
Commented by Rasheed.Sindhi last updated on 03/Feb/19
$$\mathcal{L}{o}\mathcal{T}\:{o}\mathcal{F}\:\mathcal{T}{han}\mathcal{K}{s}\:\:\mathcal{S}{i}\mathcal{R}! \\ $$
Commented by mr W last updated on 03/Feb/19
$${thanks}\:{for}\:{reviewing}\:{sir}! \\ $$
