Question Number 54341 by Meritguide1234 last updated on 02/Feb/19

Answered by iv@0uja last updated on 03/Feb/19
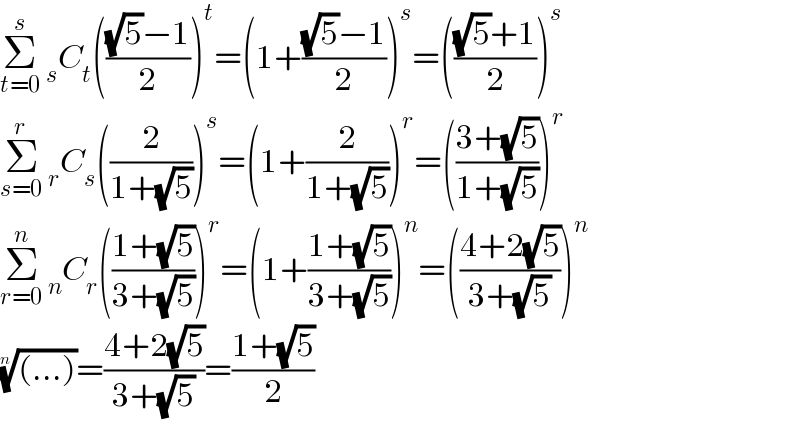
$$\underset{{t}=\mathrm{0}} {\overset{{s}} {\sum}}\:_{{s}} {C}_{{t}} \left(\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}}\right)^{{t}} =\left(\mathrm{1}+\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}}\right)^{{s}} =\left(\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{2}}\right)^{{s}} \\ $$$$\underset{{s}=\mathrm{0}} {\overset{{r}} {\sum}}\:_{{r}} {C}_{{s}} \left(\frac{\mathrm{2}}{\mathrm{1}+\sqrt{\mathrm{5}}}\right)^{{s}} =\left(\mathrm{1}+\frac{\mathrm{2}}{\mathrm{1}+\sqrt{\mathrm{5}}}\right)^{{r}} =\left(\frac{\mathrm{3}+\sqrt{\mathrm{5}}}{\mathrm{1}+\sqrt{\mathrm{5}}}\right)^{{r}} \\ $$$$\underset{{r}=\mathrm{0}} {\overset{{n}} {\sum}}\:_{{n}} {C}_{{r}} \left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{3}+\sqrt{\mathrm{5}}}\right)^{{r}} =\left(\mathrm{1}+\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{3}+\sqrt{\mathrm{5}}}\right)^{{n}} =\left(\frac{\mathrm{4}+\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{3}+\sqrt{\mathrm{5}}}\right)^{{n}} \\ $$$$\sqrt[{{n}}]{\left(…\right)}=\frac{\mathrm{4}+\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{3}+\sqrt{\mathrm{5}}}=\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$
Commented by Meritguide1234 last updated on 03/Feb/19

$$\mathrm{nice} \\ $$
