Question-54396

Question Number 54396 by mr W last updated on 03/Feb/19

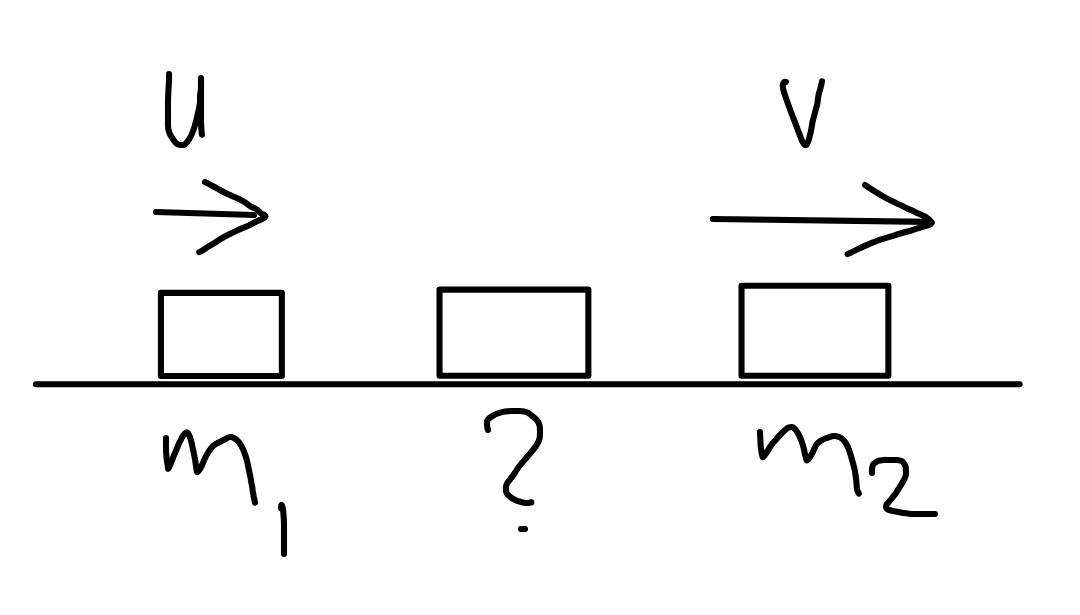
Commented by mr W last updated on 03/Feb/19

block 1 with mass m_1 moves with velocity u towards block 2 with mass m_2 . a third block is placed between them. find the mass of the third block such that the velocity of block 2 is maximum. find also v_(max) . case 1: all collisions are elastic. case 2: all collisions have a coefficient of restitution of e. what if we place more than one block between them?

$${block}\:\mathrm{1}\:{with}\:{mass}\:{m}_{\mathrm{1}} \:{moves}\:{with} \\ $$$${velocity}\:{u}\:{towards}\:{block}\:\mathrm{2}\:{with}\:{mass} \\ $$$${m}_{\mathrm{2}} .\:{a}\:{third}\:{block}\:{is}\:{placed}\:{between}\:{them}. \\ $$$${find}\:{the}\:{mass}\:{of}\:{the}\:{third}\:{block}\:{such} \\ $$$${that}\:{the}\:{velocity}\:{of}\:\:{block}\:\mathrm{2}\:{is}\:{maximum}. \\ $$$${find}\:{also}\:{v}_{{max}} . \\ $$$${case}\:\mathrm{1}:\:{all}\:{collisions}\:{are}\:{elastic}. \\ $$$${case}\:\mathrm{2}:\:{all}\:{collisions}\:{have}\:{a}\:{coefficient} \\ $$$${of}\:{restitution}\:{of}\:{e}. \\ $$$${what}\:{if}\:{we}\:{place}\:{more}\:{than}\:{one}\:{block} \\ $$$${between}\:{them}? \\ $$

Answered by mr W last updated on 06/Feb/19

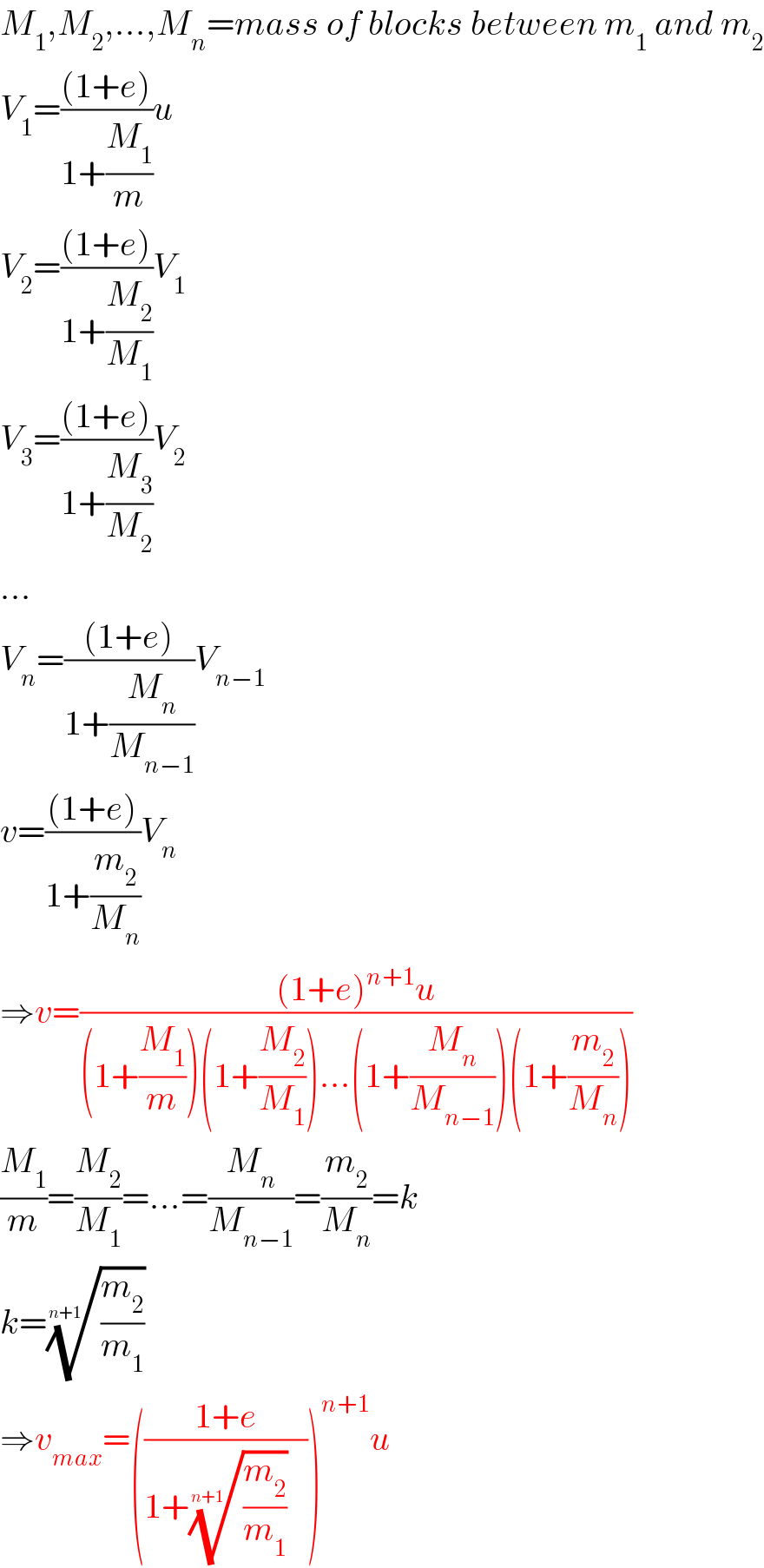
M_1 ,M_2 ,...,M_n =mass of blocks between m_1 and m_2 V_1 =(((1+e))/(1+(M_1 /m)))u V_2 =(((1+e))/(1+(M_2 /M_1 )))V_1 V_3 =(((1+e))/(1+(M_3 /M_2 )))V_2 ... V_n =(((1+e))/(1+(M_n /M_(n−1) )))V_(n−1) v=(((1+e))/(1+(m_2 /M_n )))V_n ⇒v=(((1+e)^(n+1) u)/((1+(M_1 /m))(1+(M_2 /M_1 ))...(1+(M_n /M_(n−1) ))(1+(m_2 /M_n )))) (M_1 /m)=(M_2 /M_1 )=...=(M_n /M_(n−1) )=(m_2 /M_n )=k k=((m_2 /m_1 ))^(1/(n+1)) ⇒v_(max) =(((1+e)/(1+((m_2 /m_1 ))^(1/(n+1)) )))^(n+1) u

$${M}_{\mathrm{1}} ,{M}_{\mathrm{2}} ,…,{M}_{{n}} ={mass}\:{of}\:{blocks}\:{between}\:{m}_{\mathrm{1}} \:{and}\:{m}_{\mathrm{2}} \\ $$$${V}_{\mathrm{1}} =\frac{\left(\mathrm{1}+{e}\right)}{\mathrm{1}+\frac{{M}_{\mathrm{1}} }{{m}}}{u} \\ $$$${V}_{\mathrm{2}} =\frac{\left(\mathrm{1}+{e}\right)}{\mathrm{1}+\frac{{M}_{\mathrm{2}} }{{M}_{\mathrm{1}} }}{V}_{\mathrm{1}} \\ $$$${V}_{\mathrm{3}} =\frac{\left(\mathrm{1}+{e}\right)}{\mathrm{1}+\frac{{M}_{\mathrm{3}} }{{M}_{\mathrm{2}} }}{V}_{\mathrm{2}} \\ $$$$… \\ $$$${V}_{{n}} =\frac{\left(\mathrm{1}+{e}\right)}{\mathrm{1}+\frac{{M}_{{n}} }{{M}_{{n}−\mathrm{1}} }}{V}_{{n}−\mathrm{1}} \\ $$$${v}=\frac{\left(\mathrm{1}+{e}\right)}{\mathrm{1}+\frac{{m}_{\mathrm{2}} }{{M}_{{n}} }}{V}_{{n}} \\ $$$$\Rightarrow{v}=\frac{\left(\mathrm{1}+{e}\right)^{{n}+\mathrm{1}} {u}}{\left(\mathrm{1}+\frac{{M}_{\mathrm{1}} }{{m}}\right)\left(\mathrm{1}+\frac{{M}_{\mathrm{2}} }{{M}_{\mathrm{1}} }\right)…\left(\mathrm{1}+\frac{{M}_{{n}} }{{M}_{{n}−\mathrm{1}} }\right)\left(\mathrm{1}+\frac{{m}_{\mathrm{2}} }{{M}_{{n}} }\right)} \\ $$$$\frac{{M}_{\mathrm{1}} }{{m}}=\frac{{M}_{\mathrm{2}} }{{M}_{\mathrm{1}} }=…=\frac{{M}_{{n}} }{{M}_{{n}−\mathrm{1}} }=\frac{{m}_{\mathrm{2}} }{{M}_{{n}} }={k} \\ $$$${k}=\sqrt[{{n}+\mathrm{1}}]{\frac{{m}_{\mathrm{2}} }{{m}_{\mathrm{1}} }} \\ $$$$\Rightarrow{v}_{{max}} =\left(\frac{\mathrm{1}+{e}}{\mathrm{1}+\sqrt[{{n}+\mathrm{1}}]{\frac{{m}_{\mathrm{2}} }{{m}_{\mathrm{1}} }}}\right)^{{n}+\mathrm{1}} {u} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply