Question Number 54526 by Gulay last updated on 05/Feb/19
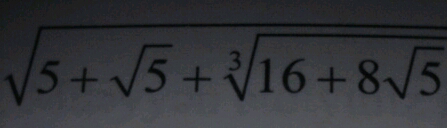
Commented by Gulay last updated on 05/Feb/19

$$\mathrm{sir}\:\mathrm{plz}\:\mathrm{help}\:\mathrm{me} \\ $$$$ \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 05/Feb/19
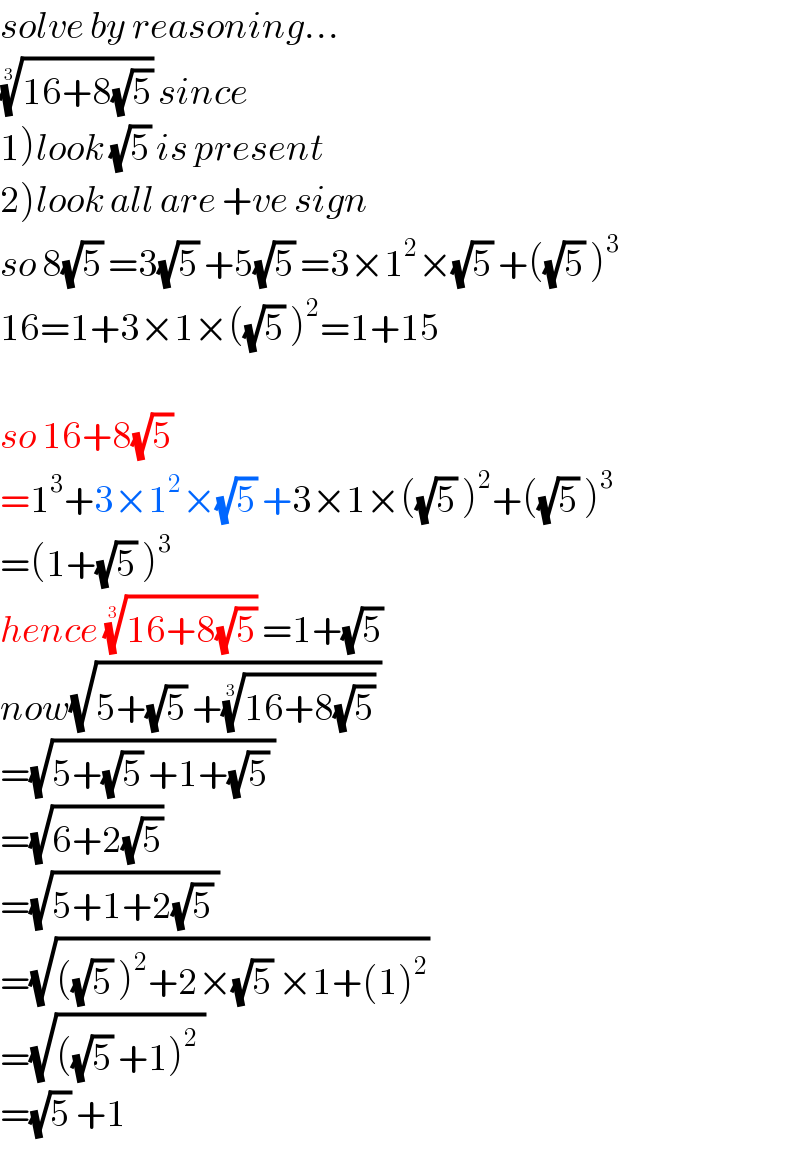
$${solve}\:{by}\:{reasoning}… \\ $$$$\sqrt[{\mathrm{3}}]{\mathrm{16}+\mathrm{8}\sqrt{\mathrm{5}}}\:{since} \\ $$$$\left.\mathrm{1}\right){look}\:\sqrt{\mathrm{5}}\:{is}\:{present} \\ $$$$\left.\mathrm{2}\right){look}\:{all}\:{are}\:+{ve}\:{sign} \\ $$$${so}\:\mathrm{8}\sqrt{\mathrm{5}}\:=\mathrm{3}\sqrt{\mathrm{5}}\:+\mathrm{5}\sqrt{\mathrm{5}}\:=\mathrm{3}×\mathrm{1}^{\mathrm{2}} ×\sqrt{\mathrm{5}}\:+\left(\sqrt{\mathrm{5}}\:\right)^{\mathrm{3}} \\ $$$$\mathrm{16}=\mathrm{1}+\mathrm{3}×\mathrm{1}×\left(\sqrt{\mathrm{5}}\:\right)^{\mathrm{2}} =\mathrm{1}+\mathrm{15} \\ $$$$ \\ $$$${so}\:\mathrm{16}+\mathrm{8}\sqrt{\mathrm{5}}\: \\ $$$$=\mathrm{1}^{\mathrm{3}} +\mathrm{3}×\mathrm{1}^{\mathrm{2}} ×\sqrt{\mathrm{5}}\:+\mathrm{3}×\mathrm{1}×\left(\sqrt{\mathrm{5}}\:\right)^{\mathrm{2}} +\left(\sqrt{\mathrm{5}}\:\right)^{\mathrm{3}} \\ $$$$=\left(\mathrm{1}+\sqrt{\mathrm{5}}\:\right)^{\mathrm{3}} \\ $$$${hence}\:\sqrt[{\mathrm{3}}]{\mathrm{16}+\mathrm{8}\sqrt{\mathrm{5}}}\:=\mathrm{1}+\sqrt{\mathrm{5}}\: \\ $$$${now}\sqrt{\mathrm{5}+\sqrt{\mathrm{5}}\:+\sqrt[{\mathrm{3}}]{\mathrm{16}+\mathrm{8}\sqrt{\mathrm{5}}}\:} \\ $$$$=\sqrt{\mathrm{5}+\sqrt{\mathrm{5}}\:+\mathrm{1}+\sqrt{\mathrm{5}}\:} \\ $$$$=\sqrt{\mathrm{6}+\mathrm{2}\sqrt{\mathrm{5}}}\: \\ $$$$=\sqrt{\mathrm{5}+\mathrm{1}+\mathrm{2}\sqrt{\mathrm{5}}\:} \\ $$$$=\sqrt{\left(\sqrt{\mathrm{5}}\:\right)^{\mathrm{2}} +\mathrm{2}×\sqrt{\mathrm{5}}\:×\mathrm{1}+\left(\mathrm{1}\right)^{\mathrm{2}} }\: \\ $$$$=\sqrt{\left(\sqrt{\mathrm{5}}\:+\mathrm{1}\right)^{\mathrm{2}} \:} \\ $$$$=\sqrt{\mathrm{5}}\:+\mathrm{1} \\ $$
Commented by Gulay last updated on 05/Feb/19
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much}\:\mathrm{sir} \\ $$
